ПРОГНОЗИРОВАНИЕ ТОЧНОСТИ ФОРМЫ ПЛОСКИХ ДЕТАЛЕЙ ИЗ ЗАКАЛЕННЫХ СТАЛЕЙ ПРИ МАЯТНИКОВОМ ШЛИФОВАНИИ ПЕРИФЕРИЕЙ АБРАЗИВНОГО КРУГА
Солер Я.И.1, Нгуен Ван Ле2, Нгуен Чи Киен3
1Кандидат технических наук, доцент; 2аспирант, 3студент, Иркутский государственный технический университет
ПРОГНОЗИРОВАНИЕ ТОЧНОСТИ ФОРМЫ ПЛОСКИХ ДЕТАЛЕЙ ИЗ ЗАКАЛЕННЫХ СТАЛЕЙ ПРИ МАЯТНИКОВОМ ШЛИФОВАНИИ ПЕРИФЕРИЕЙ АБРАЗИВНОГО КРУГА
Аннотация
Установлено, что при оценке точности формы плоских деталей из различных закаленных сталей целесообразно воспользоваться средними арифметическими и квадратичными показателями, содержащими наиболее полную информацию о всей шлифуемой поверхности.
Ключевые слова: шлифование, статистика, среднее, медиана, отклонение от плоскостности.
Soler Ya.I.1, Nguyen Van Le2, Nguyen Chi Kien3
1Candidate of technical sciences, associate professor; 2postgraduate student, 3student, Irkutsk state technical university
PREDICTION OF SHAPE PRECISION OF HARDENED STEEL FLAT PARTS AT PENDULAR GRINDING WITH PERIPHERY OF THE ABRASIVE WHEEL
Abstract
There is estimation of complex of hardened steel flat parts when use of the arithmetic and quadratic mean marks with most complete data of grinded surface is expedient.
Keywords: grinding, statistics, mean, median, flatness.
Отклонение погрешностей формы оказывает непосредственное воздействие на пространственное расположение деталей, трудоемкость и точность сборки. В некоторых случаях макрогеометрия поверхности может оказаться более значимой, чем отклонения размеров. Сказанное в полной мере относится к ответственным высоконагруженным деталям силового набора летательных аппаратов, большинство из которых изготавливаются из высокопрочных легированных сталей. Их обработка на завершающем этапе технологического процесса чаще всего завершается шлифованием сопрягаемых поверхностей. Особенности данной операции обусловлены абразивным инструментом, режущие способности которого не представляется охарактеризовать некоторой детерминированной величиной, как принято при лезвийной обработке. В черепке круга абразивные зерна имеют произвольную форму и неориентированное расположение. Это приводит к существенному рассеянию углов резания, количества зерен на единицу площади его рабочей поверхности и их расположения на различных уровнях в радиальном и осевом направлениях. Перечисленные явления носят случайный характер и их изучение целесообразно вести с привлечением теоретико-вероятностных методов [1]. Для снижения трудоемкости вычислений при принятии статистических гипотез в работе использована программа Statistica 6.1.478.
Статистические методы позволяют изучать е-ые независимые последовательности наблюдений
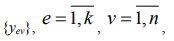 (1)
(1)
которые желательно представлять выборками равного объема n.
По методам интерпретации (1) разделяются на параметрические и непараметрические. Для их использования необходимо иметь следующую информацию по одномерному расположению частот [2; 3], ГОСТ Р ИСО 5721-1-2002:
- мерам положения (опорным значениям)
средним 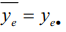 , (2)
, (2)
медианам 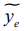 ; (3)
; (3)
- мерам рассеяния (прецизионности)
стандартам отклонений SDe, (4)
размахам Re=(ymax-ymin)e, (5)
интерквартильным широтам ИКШe=(y0,75-y0,25)e; (6)
- мерам формы расположений, в частности асимметрии (скошенности)
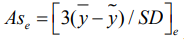 . (7)
. (7)
В одномерном и многомерном дисперсионном анализе (ОДА и МДА соответственно) знак « » в индексах опорных значений свидетельствует о проведении процедуры осреднения наблюдений по этой независимой переменной. Например, в (2) дается среднее наблюдений (1) по дублирующим опытам. Этот прием в ДА позволяет адресно отражать одновременно поиск средних по нескольким входным переменным.
» в индексах опорных значений свидетельствует о проведении процедуры осреднения наблюдений по этой независимой переменной. Например, в (2) дается среднее наблюдений (1) по дублирующим опытам. Этот прием в ДА позволяет адресно отражать одновременно поиск средних по нескольким входным переменным.
Параметрический метод базируется на распределениях частот (2), (4), (5), а альтернативное направление – на (3), (6). В теоретической статистике первая группа критериев разработана наиболее полно. В частности, это касается теории эксперимента, которая позволяет выполнять поиск моделей МДА с постоянными факторами, адекватно отражающих технологический процесс. К сожалению, сказанное имеет место только в том случае, когда наблюдения удовлетворяют требованиям нормальности и гомоскедастичности распределений (синонимы – однородность и гомогенность дисперсий). Второе ограничение к (1) должно выполняться наиболее строго. В противном случае точные параметрические оценки могут привести к принятию неверных гипотез. При шлифовании такие нарушения среди (1) встречаются довольно часто. Этот заставляет обращаться к непараметрической теории, свободной от перечисленных ограничений, которая «на своем поле» (терминология [4]) обладает большей надежностью принятия нуль-гипотезы (Н0) или ее отклонения в пользу альтернативного утверждения Н1.
Требование относительно нормальности распределений (1) в программе проверено по статистике Шапиро-Уилка (W), для которой Н0 принимается при условии:
W > 0,5. (8)
Для оценки однородности дисперсий 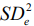 привлечены тесты (
привлечены тесты (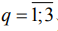 ): 1-Хартли, Кохрена и Бартлетта, представленные в программе одной группой; 2-Левене; 3-Брауна-Форсайта, которые в случае случайного рассеяния должны удовлетворять неравенству:
): 1-Хартли, Кохрена и Бартлетта, представленные в программе одной группой; 2-Левене; 3-Брауна-Форсайта, которые в случае случайного рассеяния должны удовлетворять неравенству:
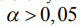 , (9)
, (9)
где 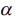 - надежность принятия Н0.
- надежность принятия Н0.
Вероятностный характер гипотез не исключает того, что отдельные решения 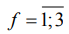 могут различаться. Окончательное решение по гомогенности
могут различаться. Окончательное решение по гомогенности 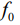 или негомогенности
или негомогенности 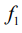 дисперсий принято из следующих соображений:
дисперсий принято из следующих соображений:
Н0 при 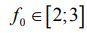 ; (10)
; (10)
Н1 при 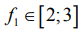 . (11)
. (11)
После обоснования метода исследования (1) процедура поиска ожидаемых средних 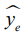 и медиан
и медиан 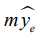 включает два последовательно выполняемых этапа. Первоначально с помощью ОДА устанавливается наличие значимого различия среди (2) и (3) без поименного их выявления. Для (2) используется аппарат классического ОДА с расчетом F–отношения, равного частному от деления среднего квадрата фактора на средний квадрат ошибки [2]. Для (3) роль ОДА формально выполняет критерий Краскелла-Уоллиса [3], в котором выступают средние квадраты ранговых сумм. В случае положительного решения проводится множественный анализ (2), (3) с предсказанием соответственно их ожидаемых величин
включает два последовательно выполняемых этапа. Первоначально с помощью ОДА устанавливается наличие значимого различия среди (2) и (3) без поименного их выявления. Для (2) используется аппарат классического ОДА с расчетом F–отношения, равного частному от деления среднего квадрата фактора на средний квадрат ошибки [2]. Для (3) роль ОДА формально выполняет критерий Краскелла-Уоллиса [3], в котором выступают средние квадраты ранговых сумм. В случае положительного решения проводится множественный анализ (2), (3) с предсказанием соответственно их ожидаемых величин 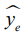 и
и 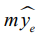 . Подробно поиск ожидаемых мер положения изложен в работах [5, 6].
. Подробно поиск ожидаемых мер положения изложен в работах [5, 6].
Для количественной оценки стабильности процесса использован индекс воспроизводимости Ср [3], который для конкретного множества 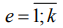 представляется выражением:
представляется выражением:
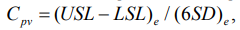 (12)
(12)
где 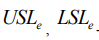 -соответственно наибольшее и наименьшее предельные отклонения е-ой последовательности (2);
-соответственно наибольшее и наименьшее предельные отклонения е-ой последовательности (2); 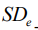 -ее выборочный стандарт.
-ее выборочный стандарт.
В работе приняты следующие неизменные условия проведения опытов: плоскошлифовальный станок модели 3Г71, круг формы 1 с размерами 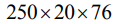 и характеристикой 34А60К6V5 (ГОСТ Р 52781 - 2007) ; скорость резания vк=35м/с; продольная подача sпр=7м/мин; поперечная подача sп=1мм/дв.ход; глубина резания t=0,015мм, межпереходный припуск z=0,15мм; СОЖ – 5%-ная эмульсия Аквол-6 (ТУ 0258-024-00148843-98), подаваемая поливом на заготовку (7-10л/мин); образцы с размерами
и характеристикой 34А60К6V5 (ГОСТ Р 52781 - 2007) ; скорость резания vк=35м/с; продольная подача sпр=7м/мин; поперечная подача sп=1мм/дв.ход; глубина резания t=0,015мм, межпереходный припуск z=0,15мм; СОЖ – 5%-ная эмульсия Аквол-6 (ТУ 0258-024-00148843-98), подаваемая поливом на заготовку (7-10л/мин); образцы с размерами 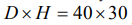 , шлифуемые по круглому торцу с повторением опытов n=30 без выхаживания. Опускание абразивного инструмента на глубину t вели в промежуток времени, когда продольный стол с заготовкой выходил из зоны резания и смещался в крайнее левое положение относительно оператора. В связи с этим его движение слева направо принято рабочим, а обратное, выполняемое без врезания в металл, – выхаживающим, окончательно формирующим макрогеометрию поверхности заготовки по схеме попутного шлифования. Последнее утверждение обусловлено тем, что абразивный инструмент имеет вращение по часовой стрелке. Переменные условия эксперимента в (1) представлены марками шлифуемых сталей (
, шлифуемые по круглому торцу с повторением опытов n=30 без выхаживания. Опускание абразивного инструмента на глубину t вели в промежуток времени, когда продольный стол с заготовкой выходил из зоны резания и смещался в крайнее левое положение относительно оператора. В связи с этим его движение слева направо принято рабочим, а обратное, выполняемое без врезания в металл, – выхаживающим, окончательно формирующим макрогеометрию поверхности заготовки по схеме попутного шлифования. Последнее утверждение обусловлено тем, что абразивный инструмент имеет вращение по часовой стрелке. Переменные условия эксперимента в (1) представлены марками шлифуемых сталей (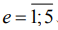 ): 1 - 30ХГСА, 2 – 30ХГСН2А-ВД, 3 – 40ХН2СМА-ВД, 4 – 13Х15Н4АМ3 (ВНС-5), 5 – 08Х15Н5Д2Т (ВНС-2).
): 1 - 30ХГСА, 2 – 30ХГСН2А-ВД, 3 – 40ХН2СМА-ВД, 4 – 13Х15Н4АМ3 (ВНС-5), 5 – 08Х15Н5Д2Т (ВНС-2).
Отклонения от прямолинейности измерены с помощью микрокатора 2-ИПМ (ТУ20234-229-89) с ценой деления 1 мкм в полярной системе координат (рисунок), начало координат которой совмещено с центром
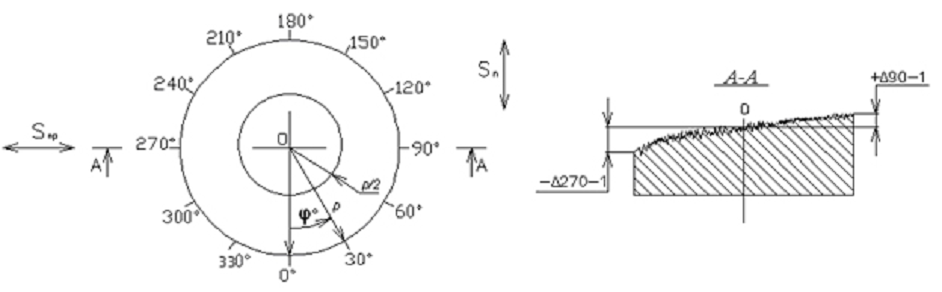
Схема измерения отклонений от прямолинейности в плоскости
заготовки. Замеры вели в 12-ти сечениях через 300 на полном радиусе D/2=20мм, который для сокращения записи представлен в виде 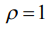 . Реальное расположение поверхности в сечениях
. Реальное расположение поверхности в сечениях 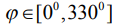 относительно начала координат
относительно начала координат 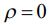 может оказаться выше (
может оказаться выше (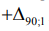 ) или ниже (
) или ниже (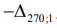 ), которые в ГОСТ 24642-81 именуются соответственно вогнутостью и выпуклостью. Полученная информация используется для повышения точности сборки соединений и машин. Однако целью данного исследования является оценка обрабатываемости различных сталей абразивным инструментом. В этом случае величины макроотклонений целесообразно предсталять одной вещественной переменной, что позволит получить поправочные коэффициенты на шлифуемые стали и ввести их в базовую модель МДА. Наблюдение макрогеометрии, представленные на рисунке, с учетом (1) преобразуем к виду
), которые в ГОСТ 24642-81 именуются соответственно вогнутостью и выпуклостью. Полученная информация используется для повышения точности сборки соединений и машин. Однако целью данного исследования является оценка обрабатываемости различных сталей абразивным инструментом. В этом случае величины макроотклонений целесообразно предсталять одной вещественной переменной, что позволит получить поправочные коэффициенты на шлифуемые стали и ввести их в базовую модель МДА. Наблюдение макрогеометрии, представленные на рисунке, с учетом (1) преобразуем к виду 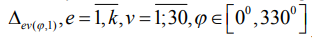 . Полученные отклонения от прямолинейности в плоскости после смены точки отчета находим из выражений (рисунок):
. Полученные отклонения от прямолинейности в плоскости после смены точки отчета находим из выражений (рисунок):
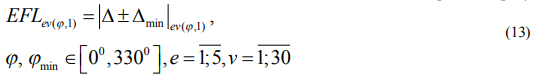
где 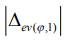 - модуль отклонения от прямолинейности для фиксированных
- модуль отклонения от прямолинейности для фиксированных 
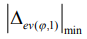 - модуль минимального отклонения от прямолинейности при варьировании
- модуль минимального отклонения от прямолинейности при варьировании 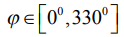 для постоянных e и v.
для постоянных e и v.
В (13) берется знак «+» при разноименных частных видах отклонений от прямолинейности и соответственно знак «-», если обе составляющие (13) находятся одновременно выше или ниже точки 0. Находим среднее по v для всех сечений (13): 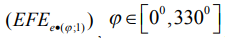 . Наибольшая из полученных величин по ГОСТ 24642-81 принимается в качестве отклонения от плоскостности:
. Наибольшая из полученных величин по ГОСТ 24642-81 принимается в качестве отклонения от плоскостности:
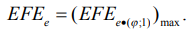 (14)
(14)
Одновременно в работе воспользовались дополнительными параметрами отклонений от плоскостности (ГОСТ 24642-81):
- средним арифметическим
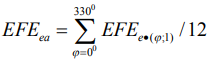 , (15)
, (15)
- средним квадратичным
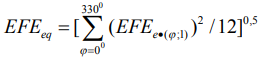 . (16)
. (16)
При использовании (15), (16) отклонение (14) в дальнейшем будем именовать наибольшим и дополним индексом «max», т.е. (14) получит обозначение - EFEemax. Для формализации информации дополнительные индексы в (14) – (16) будем именовать через  : EFEej, 1 - max, 2 - a, 3 - q. Допуск на отклонение от плоскостности TFE принят для нормальной относительной геометрической точности (ГОСТ 24643-81): TFE=0,6T, где Т – допуск на размер детали.
: EFEej, 1 - max, 2 - a, 3 - q. Допуск на отклонение от плоскостности TFE принят для нормальной относительной геометрической точности (ГОСТ 24643-81): TFE=0,6T, где Т – допуск на размер детали.
Влияние непараметрического метода на меры положений оцениваем медианными коэффициентами при одноименных  :
:
- для отклонений от прямолинейности при
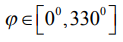

- для отклонений от плоскостности при
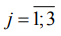

Величины (17), (19) характеризуют медианные коэффициенты, полученные по опытным данным, а (18), (20) - по их прогнозируемым аналогам. В качестве базового материала принята сталь 30ХГСА (е=1), по отношению к которой обрабатываемость остальных сталей 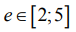 оценивалась коэффициентами отклонений от плоскостности при одноименных
оценивалась коэффициентами отклонений от плоскостности при одноименных 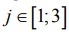 :
:

Приняв в (12) предельные отклонения от прямолинейности равными, упростим (22) и представим коэффициенты стабильности для каждого 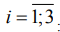 :
:
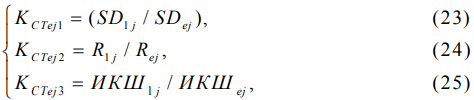
которые характеризуют меры рассеяния (4) - (6) для 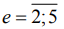 .
.
Величины (23) – (25), меньшие единицы, свидетельствуют о том, что шлифование базовых деталей 30ХГСА (е=1) протекает с наибольшей прецизионностью процесса, а при 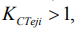 напротив в условиях наименьшей его воспроизводимостью по отношению к остальным деталям
напротив в условиях наименьшей его воспроизводимостью по отношению к остальным деталям 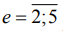 .
.
По критерию Шапиро-Уилка проанализированы распределения 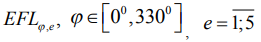 в количестве N=12×5=60. При этом только в двух случаях из 60-ти принята гипотеза Н0 при минимальной надежности α=0,52 для
в количестве N=12×5=60. При этом только в двух случаях из 60-ти принята гипотеза Н0 при минимальной надежности α=0,52 для 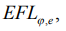 : φ=2400, е=5 и φ=2700, е=1. Проверку гомогенности дисперсий по сечениям
: φ=2400, е=5 и φ=2700, е=1. Проверку гомогенности дисперсий по сечениям 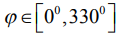 вели для всех марок сталей
вели для всех марок сталей 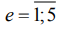 одновременно. Установлено, что Н0 по (9) с учетом критериев
одновременно. Установлено, что Н0 по (9) с учетом критериев 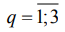 приняты по следующим φ: 00, 300, 1200, 3000 (4 случая) – по критериям q=1; 00, 300, 1200, 2700, 3000 (5 случаев) – по q=2;
приняты по следующим φ: 00, 300, 1200, 3000 (4 случая) – по критериям q=1; 00, 300, 1200, 2700, 3000 (5 случаев) – по q=2; 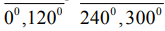 (8 случаев) – по q=3. В целом, Н0 по (10) следует отклонить, а интерпретацию (1) следует вести с привлечением непараметрического метода.
(8 случаев) – по q=3. В целом, Н0 по (10) следует отклонить, а интерпретацию (1) следует вести с привлечением непараметрического метода.
В таблице 1 представлены опытные и ожидаемые меры положения макроотклонений при шлифовании базовой стали, которые востребованы для обоих методов статистики. Опытные и прогнозируемые средние носят информационный характер и позволяют убедиться в целесообразности использования непараметрических статистик. По опорным значениям в сечениях 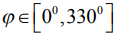 просчитаны медианные коэффициенты (17) и (18) и представлены отклонения от плоскостности по (14) – (16). Сопоставление опытных мер положения (2) и (3) в (7) показало, что из 12-ти анализируемых сечений распределения (1) имеют положительный эксцесс в пяти случаях, при φ=3000 асимметрия
просчитаны медианные коэффициенты (17) и (18) и представлены отклонения от плоскостности по (14) – (16). Сопоставление опытных мер положения (2) и (3) в (7) показало, что из 12-ти анализируемых сечений распределения (1) имеют положительный эксцесс в пяти случаях, при φ=3000 асимметрия 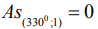 , в остальных сечениях
, в остальных сечениях 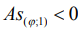 . Различие между опытными (2), (3) при всех φ, за исключением φ=600, находится в пределах одной геометрической точности. В отмеченном сечении опытная медиана оказалась больше средней в 1,17 раза и вышла за пределы допуска TFL6 на один квалитет. Относительно прогнозируемых медиан следует отметить, что их величины
. Различие между опытными (2), (3) при всех φ, за исключением φ=600, находится в пределах одной геометрической точности. В отмеченном сечении опытная медиана оказалась больше средней в 1,17 раза и вышла за пределы допуска TFL6 на один квалитет. Относительно прогнозируемых медиан следует отметить, что их величины  в девяти случаях из 12-ти предсказаны больше своих параметрических аналогов
в девяти случаях из 12-ти предсказаны больше своих параметрических аналогов 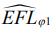 , хотя и остались в том же квалитете геометрической точности с меньшей надежностью. Медианные коэффициенты (17), (18), представленные по опытным и ожидаемым мерам положения, могут различаться не только на количественном уровне, но и на качественном. В первом случае имеем результаты следующего вида (таблица 1): Км(1;60)=1,17, а
, хотя и остались в том же квалитете геометрической точности с меньшей надежностью. Медианные коэффициенты (17), (18), представленные по опытным и ожидаемым мерам положения, могут различаться не только на количественном уровне, но и на качественном. В первом случае имеем результаты следующего вида (таблица 1): Км(1;60)=1,17, а 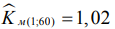 . При качественном различии (17) их
. При качественном различии (17) их
Таблица 1 – Опытные и ожидаемые меры положения отклонений от прямолинейности и плоскостности и медианные коэффициенты (17), (18) при шлифовании деталей 30ХГСА
|
φ0 |
EFLφ1 (TFL), мкм |
Км(1φ) по (17) |
по (18) |
|||
|
|
|
|
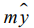 |
|||
|
0 |
9,13 (6) |
8,51 (6) |
9,00 (6) |
8,75 (6) |
0,96 |
1,03 |
|
30 |
8,84 (6) |
8,91 (6) |
10,00 (6) |
9,25 (6) |
1,13 |
1,04 |
|
60 |
9,40 (6) |
9,67 (6) |
11,00 (7) |
9,88 (6) |
1,17 |
1,02 |
|
90 |
10,17 (7) |
10,84 (7) |
11,00 (7) |
11,50 (7) |
1,08 |
1,06 |
|
120 |
11,17 (7) |
11,09 (7) |
11,50 (7) |
11,12 (7) |
1,03 |
1,00 |
|
150 |
11,10 (7) |
11,95 (7) |
11,50 (7) |
11,50 (7) |
1,04 |
0,96 |
|
180 |
10,80 (7) |
10,88 (7) |
10,00 (6) |
10,67 (7) |
0,93 |
0,98 |
|
210 |
9,90 (6) |
9,57 (6) |
10,00 (6) |
9,75 (6) |
1,01 |
1,02 |
|
240 |
9,93 (6) |
9,83 (6) |
9,50 (6) |
9,62 (6) |
0,96 |
0,98 |
|
270 |
8,10(6) |
7,34 (6) |
8,00 (6) |
7,75 (6) |
0,99 |
1,06 |
|
300 |
7,00 (6) |
6,81 (6) |
7,00 (6) |
6,83 (6) |
1,00 |
1,00 |
|
330 |
7,40 (6) |
7,50 (6) |
7,00 (6) |
7,80 (6) |
0,95 |
1,04 |
|
EFE1max (TFE) |
11,17 (7) |
11,95 (6) |
11,50 (7) |
11,50 (7) |
- |
- |
|
EFE1a (TFE) |
9,41 (6) |
9,41 (6) |
9,62 (6) |
9,54 (6) |
- |
- |
|
EFE1q (TFE) |
9,51 (6) |
9,54 (6) |
9,75 (6) |
9,65 (6) |
- |
- |
использование в базовых моделях МДА может сопровождаться уменьшением макрогеометрии в плоскости, а по (18) – напротив, их ростом (таблица 1, φ=1500) или наоборот (φ=3000). Отмеченные результаты позволяют сделать
вывод в пользу привлечения статистических методов для изучения точности формы шлифованных деталей.
Отклонения от плоскостности деталей 30ХГСА, просчитанные по (19), (20) для опытных мер положения (2), (3) и их ожидаемым аналогам, представлены в нижней части таблицы 1 и соответствуют: TFE7 – по показателю EFE11 (14) и TFE6 – для (15), (16). При этом (15), (16) оказались практически равными, но меньше наибольшего показателя (14) в 1,17-1,27 раза.
Таблица 2 – Влияние материала детали на отклонения от плоскостности
|
Показатели отклонений от плоскостности |
Отклонения от плоскостности (TFE), мкм |
||||
|
Марки сталей |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
|
11,50 (7) |
11,50 (7) |
13,25 (7) |
13,25 (7) |
7,33 (6) |
|
|
9,54 (6) |
9,36 (6) |
10,38 (7) |
10,51 (7) |
5,66 (5) |
|
|
9,65 (6) |
9,47 (6) |
10,46 (7) |
10,62 (7) |
5,81 (5) |
|
Поправочные коэффициенты |
|||||
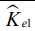 |
1,00 |
1,00 |
1,15 |
1,15 |
0,64 |
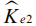 |
1,00 |
0,98 |
1,09 |
1,10 |
0,59 |
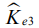 |
1,00 |
0,98 |
1,08 |
1,10 |
0,60 |
|
Примечание: стали е – 1 – 30ХГСА, 2 – 30ХГСН2А-ВД, 3 – 40ХН2СМА-ВД, 4 – 13Х15Н4АМ3, 5 – 08Х15Н5Д2Т |
|||||
Таблица 2 иллюстрирует результаты исследования влияния закаленных сталей 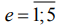 на макроотклонения поверхности деталей, которые просчитаны для ожидаемых медиан по показателям
на макроотклонения поверхности деталей, которые просчитаны для ожидаемых медиан по показателям 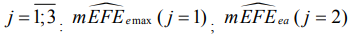 и
и 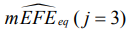 . Установлено, что наибольшая точность формы предсказана при шлифовании деталей 08Х15Н5Д2Т: (TFE)51 – 6 квалитет, (EFE)5j,
. Установлено, что наибольшая точность формы предсказана при шлифовании деталей 08Х15Н5Д2Т: (TFE)51 – 6 квалитет, (EFE)5j,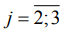 - 5 квалитет. Сопоставление ожидаемых мер положения представлено в нижней части таблицы 2 коэффициентом (21), по возрастанию величины которого снижение точности деталей прогнозируется следующим рядом: 08Х15Н5Д2Т (е=5), 30ХГСН2А-ВД (е=2), 30ХГСА (е=1), 40ХН2СМА-ВД (е=3) и 13Х15Н4АМ3 (е=4). При этом точности формы деталей
- 5 квалитет. Сопоставление ожидаемых мер положения представлено в нижней части таблицы 2 коэффициентом (21), по возрастанию величины которого снижение точности деталей прогнозируется следующим рядом: 08Х15Н5Д2Т (е=5), 30ХГСН2А-ВД (е=2), 30ХГСА (е=1), 40ХН2СМА-ВД (е=3) и 13Х15Н4АМ3 (е=4). При этом точности формы деталей 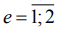 практически совпали: Кej=0,98-1,00,
практически совпали: Кej=0,98-1,00, 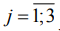 . Сказанное в полной мере относится и к деталям из закаленных сталей 40ХН2СМА-ВД и 13Х15Н4АМ3 (
. Сказанное в полной мере относится и к деталям из закаленных сталей 40ХН2СМА-ВД и 13Х15Н4АМ3 (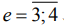 ): Ке1=1,15; Ке2=1,09-1,1 и Ке3=1,08-1,1.
): Ке1=1,15; Ке2=1,09-1,1 и Ке3=1,08-1,1.
Повышение качества изготовления деталей возможно, если технологическая система является статистически управляемой, для чего в каждый момент времени необходимо обладать информацией по опорным значениям и прецизионности (1). Наиболее часто такой подход используется при статистическом управлении процессами по двойным контрольным картам [3]. В работах [7, 8 и др.] наглядно показана его целесообразность для повышения эффективности процесса шлифования. Следует констатировать, что меры рассеяния (4), (5), используемые параметрическими статистиками, являются общепринятыми. Для них в теоретической статистике имеются коэффициенты [3], позволяющие отыскать теоретические средние квадратичных отклонений ϭe(у). Но даже в этом случае конкретно для отклонений от плоскостности остается открытым вопрос, какой из показателей (14)-(16) обладает наибольшей информативностью, т.е. несет большую информацию о поверхности. В непараметрических статистиках [4] вообще не обсуждается проблема рассеяния (1). Нами выбраны ИКШе по (6), которые содержат информацию по рассеянию 50%-тов наблюдений (1). В условиях нарушения гомоскедастичности и нормальности распределений их оценки (25) рассматриваются приоритетными, а (23), (24) – справочными, которые приведены, в частности, для того, чтобы показать опасность использования параметрических критериев «на чужом поле». Из таблицы 3 видно, что меры рассеяния отклонений от плоскостности, предсказанные по показателям (15), (16), практически совпали при постоянных е и переменных 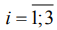 и
и 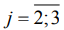 . По интерквартильным широтам при тех же условия шлифования предсказаны близкие по величинам коэффициенты стабильности
. По интерквартильным широтам при тех же условия шлифования предсказаны близкие по величинам коэффициенты стабильности 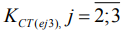 (25). Например, при шлифовании деталей 30ХГСН2А-ВД (е=2) предсказаны: 1,077 по (24) и 1,094 по (25). Одновременно отмеченные закономерности подтверждены по (25) для наибольшей величины ИКШе1 (14). По снижению коэффициентов
(25). Например, при шлифовании деталей 30ХГСН2А-ВД (е=2) предсказаны: 1,077 по (24) и 1,094 по (25). Одновременно отмеченные закономерности подтверждены по (25) для наибольшей величины ИКШе1 (14). По снижению коэффициентов 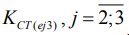 , отражающих возрастание нестабильности процесса, шлифуемые марки сталей следует расположить в следующем порядке: 13Х15Н4АМ3 (е=4); 30ХГСН2А-ВД (е=2); 30ХГСА (е=1); 08Х15Н5Д2Т (е=5), 40ХН2СМА-ВД (е=3). По параметрическим коэффициентам
, отражающих возрастание нестабильности процесса, шлифуемые марки сталей следует расположить в следующем порядке: 13Х15Н4АМ3 (е=4); 30ХГСН2А-ВД (е=2); 30ХГСА (е=1); 08Х15Н5Д2Т (е=5), 40ХН2СМА-ВД (е=3). По параметрическим коэффициентам 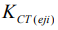
Таблица 3 – Влияние материала детали на стабильность формирования отклонений от плоскостности
|
Показатели стабильности |
Величины мер рассеяния, мкм |
||||
|
Марки сталей |
|||||
|
1 |
2 |
3 |
4 |
5 |
|
|
SDe1 |
3,714 |
5,059 |
6,383 |
3,670 |
3,978 |
|
SDe2 |
2,917 |
3,336 |
4,284 |
2,675 |
2,836 |
|
SDe3 |
2,976 |
3,479 |
4,443 |
2,746 |
2,885 |
|
Re1 |
15,000 |
21,000 |
30,000 |
15,000 |
15,000 |
|
Re2 |
12,417 |
13,000 |
19,083 |
10,417 |
10,917 |
|
Re3 |
12,672 |
13,626 |
20,185 |
10,704 |
11,079 |
|
ИКШе1 |
5,000 |
5,000 |
7,000 |
5,000 |
6,000 |
|
ИКШе2 |
3,500 |
3,250 |
4,417 |
2,833 |
3,583 |
|
ИКШе3 |
3,697 |
3,379 |
4,573 |
3,082 |
3,926 |
|
Коэффициенты стабильности (23) – (25) |
|||||
|
КСТе11 |
1,00 |
0,734 |
0,582 |
1,012 |
0,934 |
|
КСТе21 |
1,00 |
0,874 |
0,681 |
1,090 |
1,029 |
|
КСТе31 |
1,00 |
0,855 |
0,670 |
1,084 |
1,032 |
|
КСТе12 |
1,00 |
0,714 |
0,500 |
1,000 |
1,000 |
|
КСТе22 |
1,00 |
0,955 |
0,651 |
1,122 |
1,137 |
|
КСТе31 |
1,00 |
0,930 |
0,628 |
1,184 |
1,144 |
|
КСТе13 |
1,00 |
1,00 |
0,714 |
1,000 |
0,833 |
|
КСТе23 |
1,00 |
1,077 |
0,792 |
1,235 |
0,977 |
|
КСТе33 |
1,00 |
1,094 |
0,808 |
1,200 |
0,942 |
|
Примечание: стали е – 1 – 30ХГСА, 2 – 30ХГСН2А-ВД, 3 – 40ХН2СМА-ВД, 4 – 13Х15Н4АМ3, 5 – 08Х15Н5Д2Т |
|||||
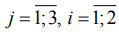 неизмененным осталось расположение сталей: 13Х15Н4АМ3, 30ХГСА и 40ХН2СМА-ВД. Оставшиеся две марки: 30ХГСН2А-ВД и 08Х15Н5Д2Т - поменялись своими местами. По терминологии, принятой при обсуждений мер положения, имеет место варьирование
неизмененным осталось расположение сталей: 13Х15Н4АМ3, 30ХГСА и 40ХН2СМА-ВД. Оставшиеся две марки: 30ХГСН2А-ВД и 08Х15Н5Д2Т - поменялись своими местами. По терминологии, принятой при обсуждений мер положения, имеет место варьирование 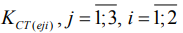 как на качественном, так и количественном уровнях.
как на качественном, так и количественном уровнях.
Результаты проведенного исследования показали, что для оценки точности формы деталей из исследуемых сталей, шлифуемых электрохромистыми корундовыми кругами нормальной пористости, следует использовать показатели EFEea (15) и EFEeq (16), содержащие наиболее полную информацию о состоянии получаемой поверхности. Их также следуют использовать для поиска поправочных коэффициентов к базовым моделям МДА, которые в исходном состоянии содержат конкретную информацию по наибольшим отклонениям от прямолинейности по всем сечением  .
.
Список литературы
Зубарев Ю.М. Теория и практика повышения эффективности шлифования материалов/ Ю.М. Зубарев, А.В. Приемышев. - СПб: Изд–во «Лань», 2010. – 304с.
Закс Л. Статистическое оценивание/ Л. Закс; пер. с нем. – М.: Статистика, 1976. – 598 с.
Уилер Д. Статистическое управление процессами/ Д. Уилер, Д. Чамберс; пер. с англ. – М.: Альпина Бизнес Букс, 2009. – 409 с.
Холлендер М. Непараметрические методы статистики/ М. Холлендер, Д. Вулф; пер. с англ. М: Финансы и статистика, 1983. – 578 с.
Солер Я.И. Исследование влияния выхаживания на микрорельеф пластин Р9М4К8 при шлифовании кругами из кубического нитрида бора/ Я.И. Солер, А.В. Прокопьева// Обработка металлов, 2009. - №1 (42). С.55-64.
Солер Я.И. Выбор абразивных кругов при плоском шлифовании деталей силового набора летательных аппаратов по критерию шероховатости поверхности/ Я.И. Солер, Д.Ю. Казимиров// Вестник машиностроения, 2010. - №3. – С.55-64.
Солер Я.И. Оценка режущих свойств кругов нового поколения «Аэробор» по критерию шероховатости при шлифовании плоских деталей основного и вспомогательного производств самолетостроительных предприятий/ Я.И. Солер [и др.]// Вестник ИрГТУ, 2013. - №4 (75). – С.43-50.
Солер Я.И. Прогнозирование шероховатости поверхности плоских деталей из закаленных сталей 30ХГСА при различном задании поперечной подачи в условиях маятникового шлифования высокопористым синтеркорундом/ Я.И. Солер, С.С. Небого, А.А. Доморат// Вестник ИрГТУ, 2013. - №7 (78). – С. 22-31.

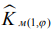
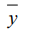
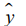
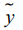
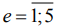
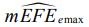 (14)
(14)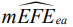 (15)
(15)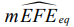 (16)
(16)