Метод прогнозирования диагностических параметров оборудования на основе генетического поиска
Метод прогнозирования диагностических параметров оборудования на основе генетического поиска
Аннотация
Целью данного исследования является разработка метода прогнозирования диагностических параметров оборудования на основе генетического поиска. Актуальность работы обусловлена возрастающей сложностью и стоимостью промышленного оборудования, что требует перехода от ремонтов по фактическому состоянию к предупредительному обслуживанию. Существующие методы прогнозирования недостаточно эффективны при работе с короткими временными рядами данных, что характерно для реальных условий эксплуатации. Для достижения поставленной цели в работе предложен трехэтапный алгоритм генетической оптимизации, включающий последовательный поиск оптимального порядка авторегрессионной модели, константы и коэффициентов авторегрессии. Разработано специализированное программное обеспечение, реализующее предложенный метод. Верификация метода проведена на реальных экспериментальных данных о температуре подшипников. Показано, что предложенный подход обеспечивает высокую точность прогноза при работе с временными рядами, позволяет адаптивно настраивать модель под конкретное оборудование. Результаты работы могут быть использованы для построения систем предупредительного обслуживания промышленного оборудования, повышения его надежности и экономической эффективности эксплуатации.
1. Введение
Современное промышленное производство характеризуется возрастающей сложностью и стоимостью оборудования, что обуславливает необходимость разработки эффективных методов прогнозирования его технического состояния. Своевременное предсказание отказов позволяет перейти от ремонтов по фактическому состоянию к предупредительному обслуживанию, что значительно повышает надежность и экономическую эффективность эксплуатации технических систем.
В научной литературе представлено большое количество исследований, посвященных методам прогнозирования диагностических параметров и отказов оборудования. Например, в работе описано прогнозирование отказов систем автоматического управления газоперекачивающих агрегатов на основе индекса технического состояния и степени риска. В статье решается задача прогнозирования остаточного ресурса подшипников по уровню вибрации механизма. Публикация посвящена применению анализа временных рядов и модели ARIMA для прогнозирования количества отказов бортового оборудования самолета A320.
В обзоре рассматриваются методы прогнозного мониторинга технического состояния электрических машин с использованием машинного обучения. Исследование предлагает метод локальной аппроксимации для прогноза нерегулярных временных рядов отказов горнотранспортных машин. В работе представлен метод прогнозирования оставшегося времени безаварийной работы нефтегазодобывающего оборудования с применением искусственных нейронных сетей. В статье предложен метод прогнозирования остаточного ресурса оборудования в условиях малой выборки данных.
В публикации проводится сравнение алгоритмов оптимизации для обучения нейронных сетей в задачах прогнозирования сбоев в промышленности. В работе предлагается метод диагностики неисправностей электродвигателей с использованием мультимодальных временных рядов. В статье рассматривается метод обнаружения отказов оборудования на основе анализа вибрационных сигналов. Публикация посвящена разработке алгоритма и системы прогнозирования отказов производственного оборудования на основе статистических данных о его эксплуатации. В отличие от других работ, в публикации , рассматривается метод статистического анализа данных об отказах оборудования атомных станций в условиях неоднородного потока событий.
Анализ литературы показал, что, несмотря на разнообразие методов, существует потребность в адаптивных, интерпретируемых и вычислительно эффективных моделях, особенно для работы с короткими временными рядами данных от оборудования.
Целью исследования является разработка метода прогнозирования диагностических параметров оборудования на основе генетического поиска оптимальных параметров авторегрессионной модели, обеспечивающего высокую точность прогноза при работе с короткими временными рядами данных.
2. Постановка задачи
Пусть дан временной ряд yt, представляющий значения диагностического параметра оборудования в моменты времени t=1, 2, …, N. Необходимо построить адаптивную авторегрессионную (AR) модель, позволяющую прогнозировать значение yt+k с заданным горизонтом прогноза k.
Адаптивная модель должна работать по принципу скользящего окна фиксированного размера r. В каждый момент времени t≥r для построения прогноза используется только последние r наблюдений ряда: {yt-r+1, yt-r+2, ..., yt}.
Параметры AR-модели {n, c, ϕ1, …, ϕn} должны адаптивно перестраиваться по событиям, минимизируя ошибку на горизонте прогноза.
3. Разработка метода прогнозирования
Для решения задачи прогнозирования параметров состояния оборудования был выбран аппарат авторегрессионных моделей временных рядов. Данный выбор обусловлен их эффективностью при работе с короткими рядами данных, интерпретируемостью результатов, низкими вычислительными затратами в режиме эксплуатации и доказанной эффективностью для описания инерционных процессов, к которым относятся процессы износа и деградации механических систем. В качестве диагностических параметров можно рассматривать среднеквадратическое значение вибрации, температуру подшипникового узла или ток потребления электродвигателя.
В рамках предлагаемого метода диагностический параметр, измеряется в дискретные моменты времени и рассматривается как временной ряд yt, где t=1, 2, ..., N. Прогнозное значение этого параметра на k шагов вперед ŷt+k вычисляется на основе линейной комбинации n предыдущих значений самого ряда:
где ŷt+k — прогнозируемое значение параметра в момент времени t+k; c – постоянная составляющая модели; φ1, φ2, …, φp — коэффициенты авторегрессии, подлежащие определению; p — порядок авторегрессионной модели, определяющий глубину исторической памяти; εt+k — ошибка прогноза в момент времени t+k.
Качество и точность прогноза при использовании AR-модели зависят от корректного определения трех групп параметров:
1) Порядок модели p. Слишком малый порядок не позволяет уловить сложные динамические закономерности процесса, в то время как избыточный порядок ведет к переобучению модели и росту ошибки на новых данных.
2) Постоянная составляющая модели c. Если постоянная составляющая c выбрана неверно, это может привести к систематическому смещению прогноза вверх или вниз, даже при правильно подобранных коэффициентах авторегрессии, что снижает общую точность модели.
3) Коэффициенты авторегрессии φi. Их значения должны быть подобраны таким образом, чтобы минимизировать расхождение между прогнозируемыми ŷt+k и фактически наблюдаемыми yt+k значениями на репрезентативной выборке данных.
Таким образом, задача построения адаптивной прогнозной модели сводится к решению задачи поиска такого набора параметров {n, c, φ1, ..., φn}, который доставляет минимум выбранному критерию качества. Для решения этой многопараметрической задачи оптимизации в работе предлагается использовать трехэтапный алгоритм на основе генетического поиска (см. рис. 1), что позволяет адаптивно настраивать модель под конкретный экземпляр оборудования и текущий режим его эксплуатации без необходимости априорного задания сложных физико-математических моделей деградации.
Данный подход позволяет разделить сложную задачу многопараметрической оптимизации на три более простые подзадачи, что значительно улучшает сходимость алгоритма и качество конечного решения.
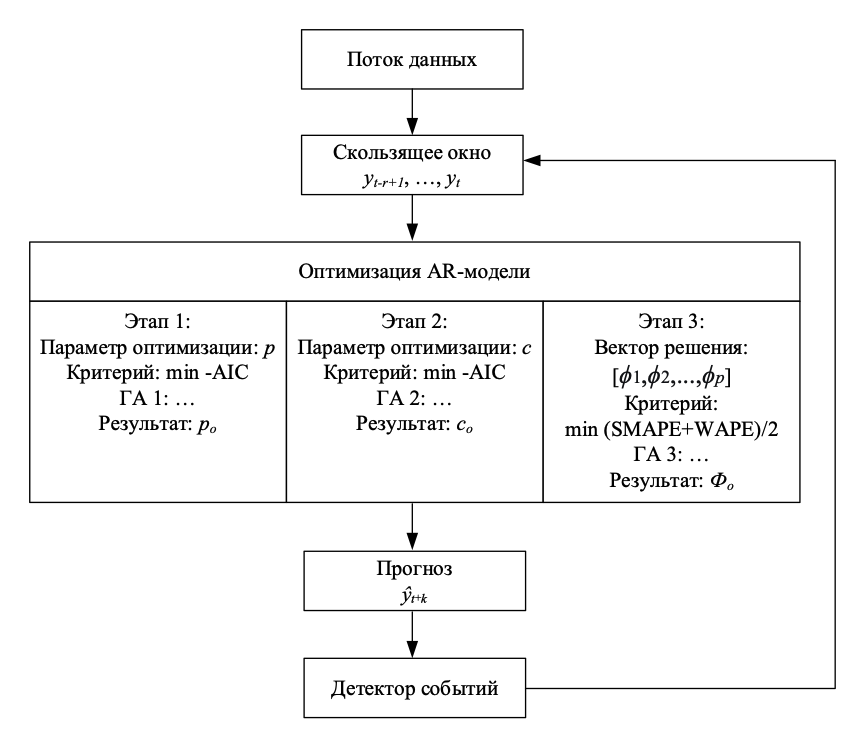
Рисунок 1 - Схема адаптивной модели прогнозирования
В предложенной схеме детектор событий функционирует как пороговый механизм, предотвращающий избыточные вычислительные затраты за счет запуска полной оптимизации только при существенном изменении динамики сигнала. Его работа основана на мониторинге статистических характеристик внутри скользящего окна данных. В качестве критерия активации может использоваться выход значений за пределы ±3σ, рассчитанные для предыдущего интервала оптимизации или устойчивое превышение ошибки прогноза над установленным порогом в течение нескольких тактов. При срабатывании любого из этих условий система интерпретирует это как «событие», указывающее на изменение режима работы оборудования, или начала фазы ускоренной деградации, и инициирует процесс полной перенастройки модели для адаптации к новым условиям.
На этапе 1 выполняется оптимизация порядка авторегрессионной модели, который обеспечивает баланс между точностью аппроксимации и сложностью модели. В алгоритме оптимизации хромосома представляет целое число p. Сначала генерируется начальная популяция размером Np1, где каждая особь представляет случайное целое число из диапазона [pmin, pmax]. При этом pmin=1, а pmax определяется вычислительными возможностями и размером скользящего окна. Для каждой особи p выполняется вычисление коэффициентов авторегрессии φ1, φ2, …, φp и константы c методом Юла-Уокера .
Затем вычисляется среднеквадратическая ошибка:
и значение критерия Акаике :
что составляет функцию оптимизации F1(p)=−AIC.
В качестве генетических операторов используется турнирная селекция, одноточечные кроссовер и равномерная мутация. Критерием остановки является максимальное количество поколений Gmax или отсутствие улучшения функции оптимизации в течение 15–20 поколений. В результате этапа 1 определяется порядок модели po.
На этапе 2 выполняется оптимизация постоянной составляющей авторегрессионной модели c при фиксированном порядке po. В алгоритме оптимизации хромосома представляет собой вещественное число c. Сначала генерируется начальная популяция размером Np2, где каждая особь представляет случайное число из диапазона [cmin, cmax]. При этом cmin=my-2σy, а cmax= my+2σy, где my, σy — математическое ожидание и стандартное отклонение временного ряда. Для каждой особи c при фиксированном po вычисляются коэффициенты авторегрессии φ1, φ2, …, φp методом Юла-Уокера. Функцию оптимизации используется такая же, как и на этапе 1 – F2(c)=−AIC. В результате этапа 2 определяется постоянная составляющая модели co.
На этапе 3 выполняется оптимизация коэффициентов авторегрессии φ1, φ2, …, φp при постоянных po и co. В алгоритме оптимизации хромосома представляет собой вектор вещественных чисел Φ=[φ1, φ2, …, φp]. Сначала генерируется начальная популяция размером Np3, где каждая особь представляет случайное число из диапазона [-1, 1]. Для каждой особи Φ выполняется расчет прогнозных значений:
расчет симметричной средней абсолютной процентной ошибки:
расчет взвешенной абсолютной процентной ошибки:
и расчет ошибки прогнозирования:
с функцией оптимизации F3(Φ)=−E.
В качестве генетических операторов используется турнирная селекция, BLX-α кроссовер с α=0,5, неравномерная мутация и элитизм на уровне 5%. В результате этапа 3 определяется оптимальный вектор коэффициентов модели Φo=[φ1o, φ2o, …, φpo].
Таким образом, в многоэтапном алгоритме оптимизации реализуется последовательность вычислений po→co→Φo, где выход каждого предыдущего этапа является входным параметром для следующего этапа. Это позволяет снизить размерность пространства поиска на каждом этапе, улучшить сходимость алгоритма, повысить устойчивость решения, сократить вычислительные затраты.
4. Программная реализация и экспериментальные исследования
Для верификации предложенного метода было разработано программное обеспечение на языке Python. Программа реализована в объектно-ориентированном стиле, что обеспечивает модульность, легкость сопровождения и возможность повторного использования компонентов. Архитектура программы разделена на несколько взаимосвязанных модулей, как представлено на рисунке 2.
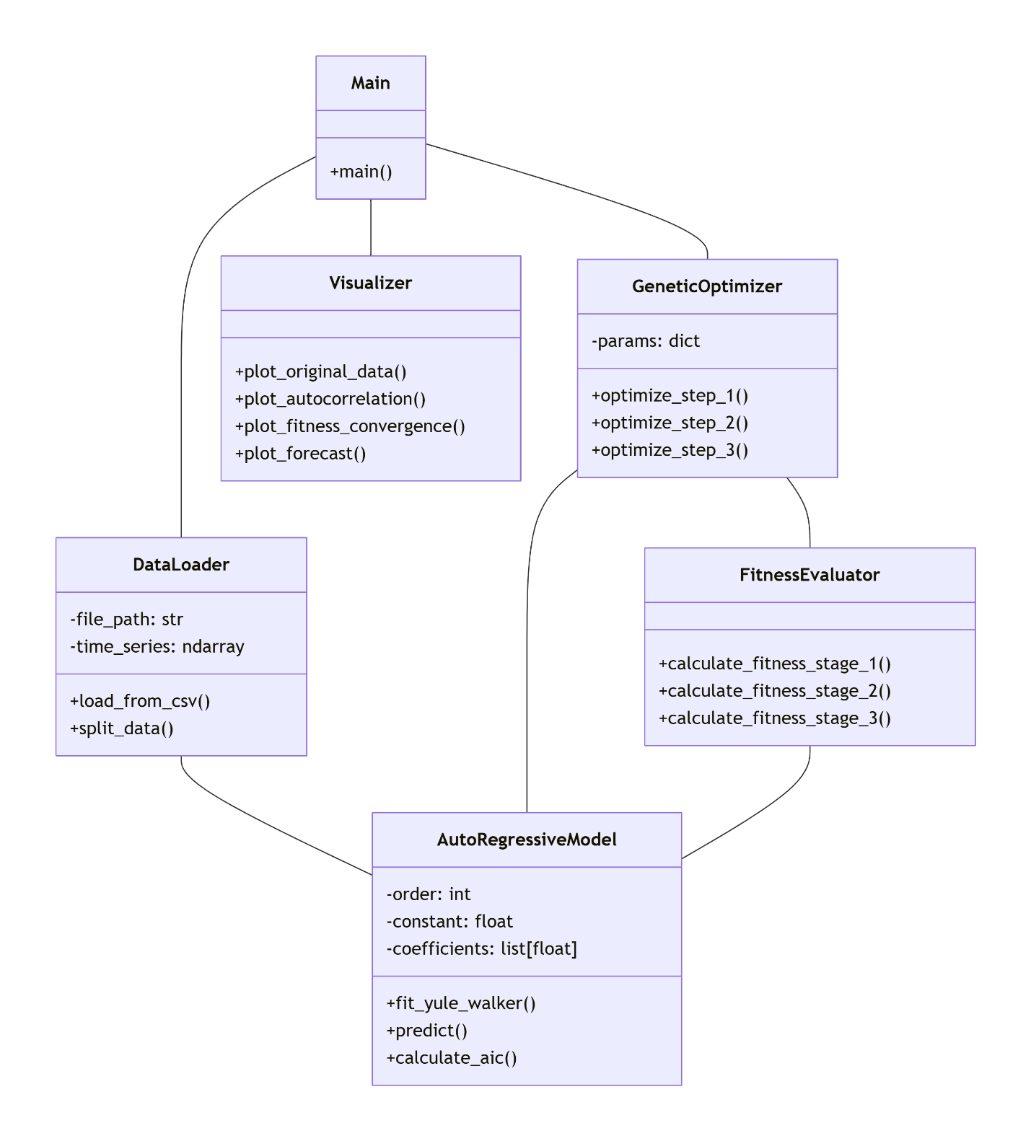
Рисунок 2 - UML-диаграмма классов программного комплекса
– Main: основной исполняемый модуль, который управляет процессом инициализации, загрузки данных, запуска оптимизации и визуализации результатов.
– DataLoader: модуль для чтения и предварительной обработки исходных данных.
– AutoRegressiveModel: модуль, содержащий класс авторегрессионной модели и методы для ее обучения и прогнозирования.
– GeneticOptimizer: модуль, реализующий алгоритм для оптимизации параметров AR-модели.
– FitnessEvaluator: модуль для расчета значений критериев на разных этапах оптимизации.
– Visualizer: модуль для построения графиков и визуализации результатов прогнозирования.
Функции модуля Main включают создание экземпляра класса DataLoader для загрузки временного ряда диагностического параметра из csv-файла; инициализацию параметров генетического алгоритма; последовательный вызов трех этапов оптимизации через класс GeneticOptimizer; использование класса Visualizer для отображения исходных данных, автокорреляционной функции, сходимости генетического алгоритма и итогового прогноза.
Функции модуля DataLoader включают чтение данных из csv-файла и преобразование их в массив; разделение временного ряда на обучающую и тестовую выборки.
Функции модуля AutoRegressiveModel включают вычисление коэффициентов модели по методу Юла-Уокера для заданного временного ряда; вычисление прогноза на основе обученной модели; расчет информационного критерия Акаике.
Функции модуля GeneticOptimizer включают оптимизацию порядка, постоянного значения и коэффициентов AR-модели. На каждом этапе используется свой тип кодирования особи, операторы кроссовера и мутации.
Модуль для расчета значений критериев содержит класс FitnessEvaluator, который инкапсулирует логику расчета целевых функций для каждого из этапов оптимизации.
Функции модуля Visualizer включают построение графика исходного временного ряда, отображение графика сходимости генетических алгоритмов и визуализацию исходных и прогнозных данных.
В ходе исследования для верификации предложенного подхода были использованы реальные экспериментальные данные о температуре подшипников, полученные в рамках открытого соревнования IEEE PHM 2012 Data Challenge . Показания температуры регистрировались с помощью датчика RTD PT100 и сохранялись с дискретностью 1 минута, что обеспечило репрезентативный временной ряд для анализа тепловых режимов работы узла в процессе его деградации вплоть до полного отказа. Временной ряд содержит более 140 тыс. измерений температуры, как представлено на рисунке 3. Использование натурных данных позволило учесть реальные нестационарные тепловые процессы и повысить достоверность экспериментальных исследований.
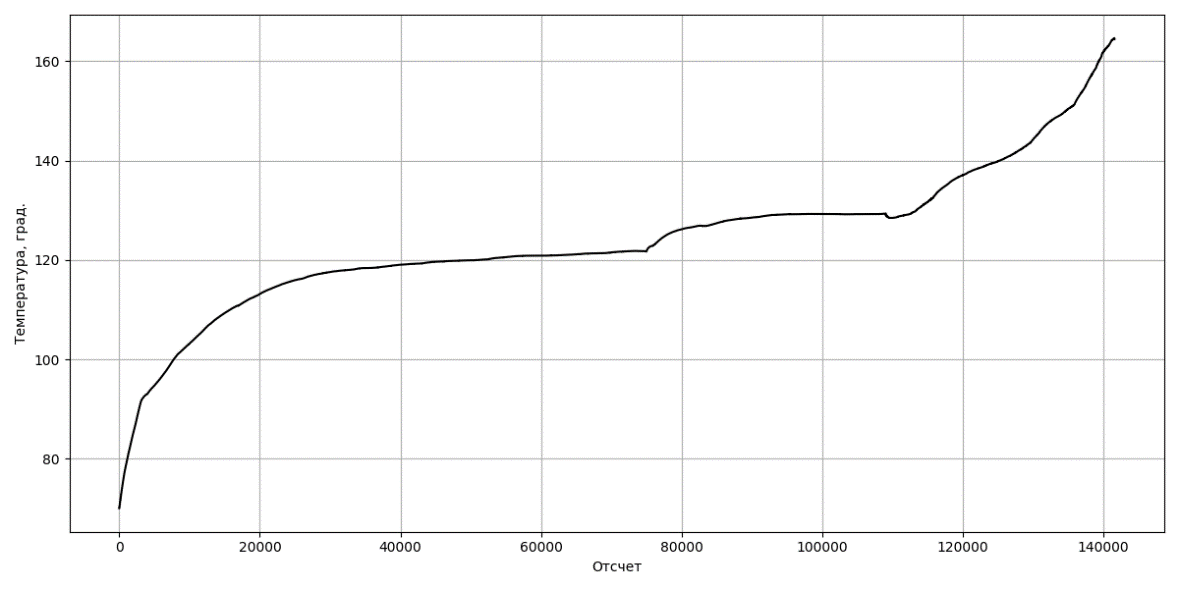
Рисунок 3 - Временной ряд изменения температуры подшипника
Результаты моделирования представлены на рисунках 4, 5. По результатам моделирования установлено, что в модели прогнозирования за 233 часа измерений температуры 495 раз изменился порядок модели в интервале [5, 40]: [5 6 7 9 10 11 13 15 17 21 23 25 27 29 33 37 39] (см. рис. 5). Суммарное время работы алгоритма оптимизации составило 1,9 часа, при средней длительности оптимизации 30 секунд. Максимальный размер скользящего окна составил rmax=312. Среднеквадратичная ошибка составила MSE = 0,006. Максимальная абсолютная ошибка составила 0,31°С.
5. Обсуждение результатов
Разработанный метод прогнозирования диагностических параметров оборудования на основе генетического поиска продемонстрировал высокую эффективность при работе с временными рядами, что подтверждено результатами эксперимента на реальных данных о температуре подшипников. Использование трёхэтапного алгоритма оптимизации позволило последовательно определять порядок модели, постоянную составляющую и коэффициенты авторегрессии.
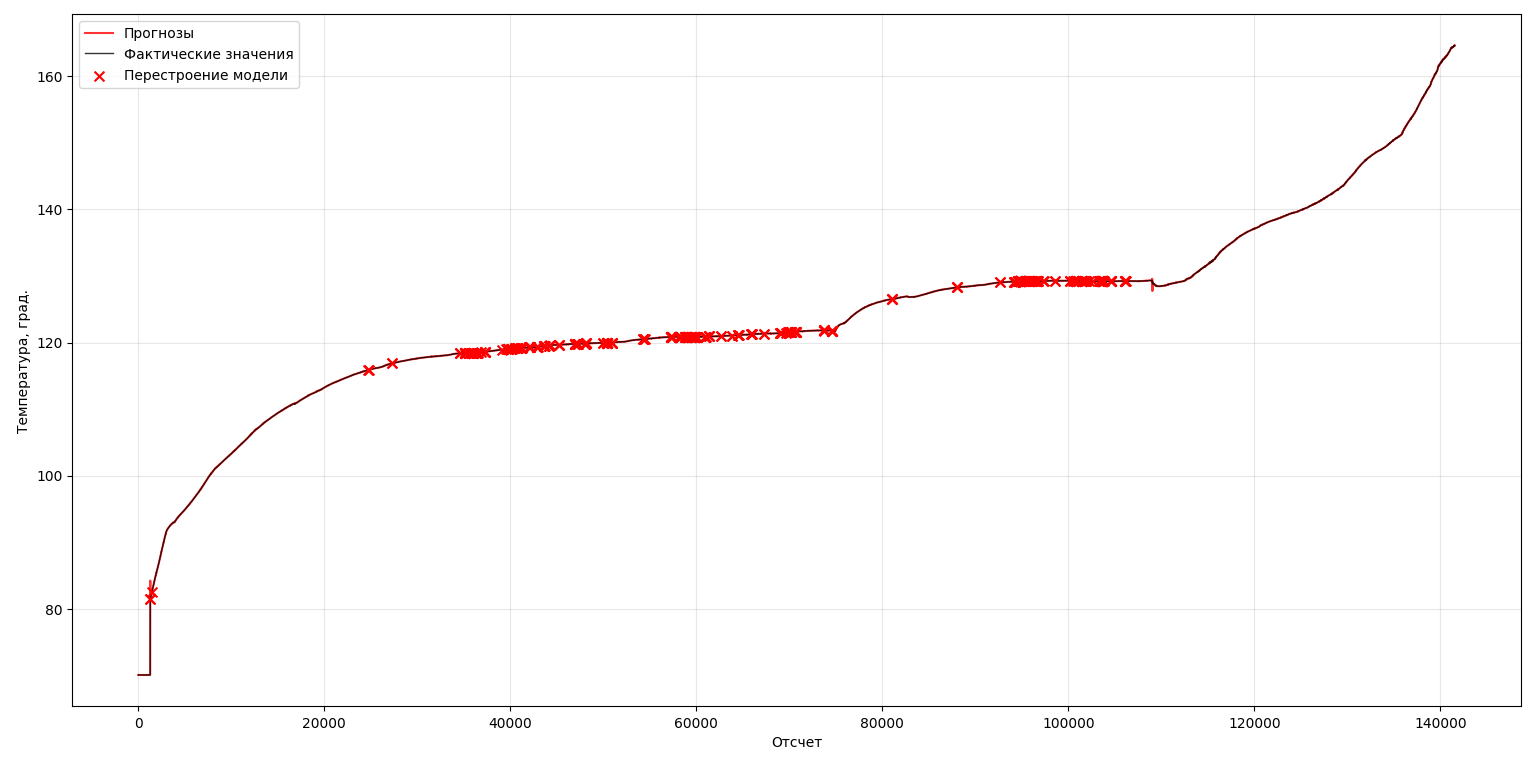
Рисунок 4 - Результаты прогнозирования изменения температуры подшипника
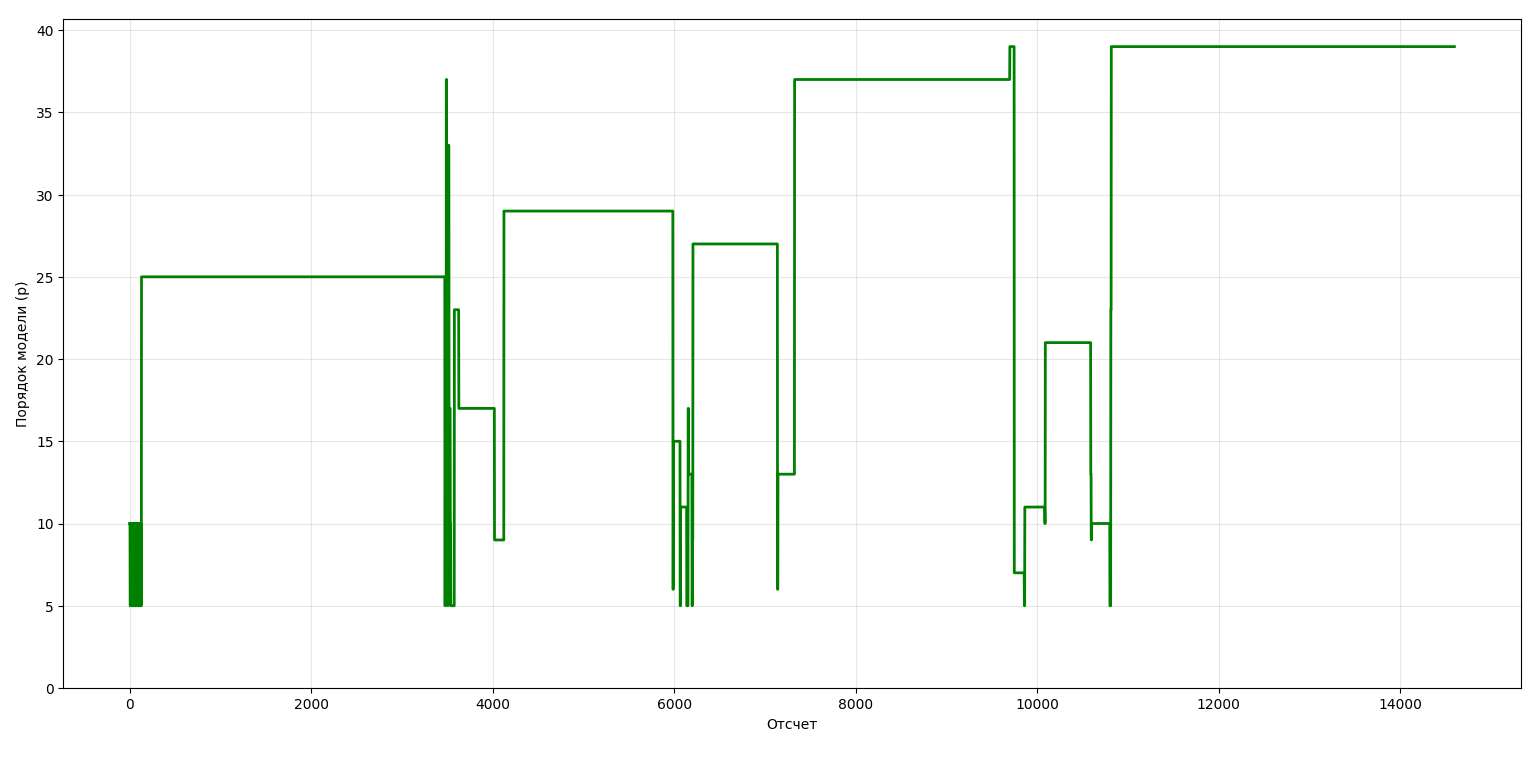
Рисунок 5 - Результаты изменения порядка модели прогнозирования
Кроме того, использование скользящего окна и детектора событий позволило минимизировать вычислительные затраты, запуская полную оптимизацию только при значительных изменениях в данных. Это делает метод применимым в реальном времени для систем предиктивного обслуживания. Сравнение с результатами моделирования, в которых использовался один генетический алгоритм для поиска всех параметров модели показало, что скорость работы предложенного метода выше на 62%.
Ограничением предложенного метода можно считать зависимость от точности задания начальных параметров генетического алгоритма, а также необходимость балансировки между точностью и вычислительной сложностью при выборе максимального порядка модели, что уточняется в результате реального применения метода.
6. Заключение
В ходе исследования разработан и верифицирован метод прогнозирования диагностических параметров оборудования на основе генетического поиска оптимальных параметров авторегрессионной модели. Предложенный трёхэтапный алгоритм позволяет эффективно решать задачу прогнозирования при работе с временными рядами, характерными для реальных условий эксплуатации промышленного оборудования.
Экспериментальная проверка на данных о температуре подшипников подтвердила высокую точность и адаптивность метода. Использование генетического поиска для оптимизации параметров модели позволило достичь баланса между точностью прогноза и вычислительной эффективностью, что делает метод применимым в системах предупредительного обслуживания.
Таким образом, предложенный подход представляет собой перспективное решение для построения интеллектуальных систем мониторинга и прогнозирования состояния оборудования, способствующее повышению его надёжности, снижению эксплуатационных затрат и переходу от реактивного к предиктивному управлению техническим состоянием. В дальнейшем метод может быть расширен за счёт интеграции с другими типами моделей, а также применения методов искусственного интеллекта для автоматизации настройки гиперпараметров генетического алгоритма.
