ПРЕДИКТИВНЫЙ РАСЧЕТ ТОЛЩИНЫ ФАЗ АЗОТИРОВАННЫХ СЛОЕВ
ПРЕДИКТИВНЫЙ РАСЧЕТ ТОЛЩИНЫ ФАЗ АЗОТИРОВАННЫХ СЛОЕВ
Научная статья
Федотова А.Д.1, *, Крукович М.Г.2
1 ORCID: 0000-0003-1547-4156;
2 ORCID: 0000-0001-5563-0930;
1, 2 Российский университет транспорта, Москва, Россия
* Корреспондирующий автор (afca23[at]mail.ru)
АннотацияПроведен анализ закономерностей протекания процессов азотирования в различных средах и экспериментально установлен порядок образования фаз. Определен параметр, комплексно характеризующий процесс азотирования, названный кинетическим коэффициентом, и установлена его температурно-временная зависимость. Предложена модель расчета толщин фаз азотированного слоя, в том числе при наличии в стали легирующих элементов. Показано, что легирующие элементы оказывает одинаковое влияние на рост слоя нитридов и α – твердого раствора при различных способах протекания процесса. Эта модель может быть использована для любых технологий азотирования в случае определения для них приведенных кинетических коэффициентов.
Ключевые слова: азотирование, кинетический коэффициент, граничные условия, толщина слоя, нитриды, α-твердый раствор, легирующие элементы, достоверность расчета.
PREDICTIVE CALCULATION OF THE PHASE THICKNESS OF NITRIDED CASES
Research article
Fedotova A.D.1, *, Krukovich M.G.2
1 ORCID: 0000-0003-1547-4156;
2 ORCID: 0000-0001-5563-0930;
1, 2 Russian university of transport, Moscow, Russia
* Corresponding author (afca23[at]mail.ru)
AbstractThe current article conducts an analysis of the regularities of the nitriding processes in various media and experimentally determines the order of phase formation. The study determined a parameter that comprehensively characterizes the nitriding process, which was called the kinetic coefficient; the study also determines its temperature-time relationship. The authors propose a model for calculating the thicknesses of the phases of nitrided cases, including the presence of alloying elements in the steel. It is shown that the alloying elements have the same effect on the growth of the nitride layer and the α - solid solution at different methods of the process. This model can be used for any nitriding technologies if the presented kinetic coefficients are determined.
Keywords: nitriding, kinetic coefficient, boundary conditions, phase thickness, nitrides, α-solid solution, alloying elements, reliability of calculation.
Введение
Азотирование является одним из эффективных методов повышения надежности и долговечности деталей и инструментов. В то же время для надежного применения процесса насыщения и азотированных слоев на практике возникает необходимость получения предварительных результатов обработки. В частности, для оценки качества упрочненных деталей, изготовленных из конструкционных сталей, важным является толщина полученного слоя. В настоящее время существуют методики расчета толщины фаз азотированного слоя, основанные на решении уравнений Фика с граничными условиями, которые позволяют определить коэффициенты диффузии азота в железе и образующихся фазах, оценить толщину образующихся слоев с допустимой достоверностью [1], [3], [4], [6]. Попытки использования этого подхода при азотировании легированных конструкционных сталей приводят к большим погрешностям (более 15%) и сводятся к группированию сталей по степени легированности при отдельных способах обработки [2], [7].
Таким образом, целью данной работы является разработка методики предварительного расчета толщины фаз азотированного слоя на конструкционных сталях с более высокой достоверностью.
В задачи работы входит исследование закономерностей протекания процессов азотирования в различных средах, моделирование и расчет ключевого параметра процесса азотирования, определение влияния содержания легирующих элементов на толщину азотированного слоя.
Методика проведения исследования
Результаты азотирования получены на техническом железе и специально выплавленных сталях с различным содержанием одного из легирующих элементов (до 6 % по массе). Выбранные количества легирующих элементов соответствуют их содержанию в большинстве конструкционных и инструментальных сталях.
Азотирование проводилось в газовой среде на основе диссоциированного аммиака, разбавленного азотом при 500 – 550 0С в течение 25 -35 ч, в расплавах солей на основе цианатов натрия и калия при температурах 550 – 570 0С в течение 1,5 ч и в газовой среде закрытых контейнеров при 500 – 550 0С в течение 5 ч. Газообразующей составляющей последней технологии являлась мочевина (100 %). Контейнеры герметизировались плавким затвором (80% SiO2 + 20% В2О3).
Исследования структуры и фазового состава получаемых азотированных слоев проводились с применением металлографического, рентгеноструктурного и дюрометрического методов анализа.
Математическое моделирование заключалось в нахождении коэффициентов диффузии азота в железе при решении уравнений Фика с граничными условиями, обеспечивающих образования различных фаз. Эмпирическое моделирование основывалось на методах аппроксимации зависимостей, принципах экстраполяции и интерполяции, принципах подобия и логики. Достоверность разработанной модели расчета была подтверждена на стандартных марках конструкционных сталей.
Разработка расчетной модели
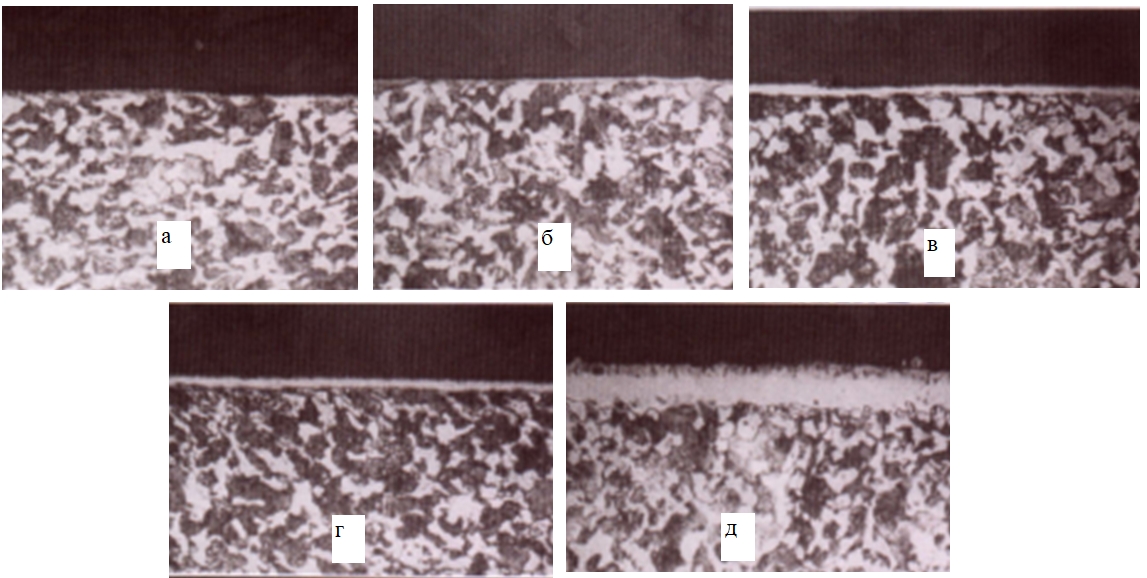
Формирование азотированного слоя во времени протекает при изменении условий на поверхности. При этом в начале образуется слой α-твердого раствора, а затем, по мере накопления азота, формируется слой нитридов. Динамика формирования слоя во времени была прослежена при азотировании в расплавах солей (Рисунок 1). Было установлено, что до образования сплошного слоя нитридов имеет место одна закономерность роста α-твердого раствора, а после образования слоя нитридов, толщиной 3 мкм – другая.
Рис. 1 – Динамика роста азотированных слоев во времени (570оС):
а – 3 мин, y_∝=100 мкм,y_γꞌ=0 мкм; б – 15 мин, y_∝=225 мкм,y_γꞌ=1 мкм; в – 25 мин, y_∝=290 мкм,y_γꞌ=3 мкм; г – 35 мин, y_∝=350 мкм,y_γꞌ=5 мкм; д – 90 мин, y_∝=550 мкм,y_γꞌ=25 мкм
Таким образом, с появлением на поверхности новой фазы, более богатой по азоту, рост предыдущей фазы замедляется. Этот факт находится в полном соответствии с величинами коэффициентов диффузии в α-твердом растворе и γꞌ фазе. На обрабатываемой поверхности устанавливается равновесие в соответствии с ее реакционной способностью между обрабатываемым металлом и средой, а на границе раздела нитрида γꞌ и α-твердого раствора устанавливается равновесие в соответствии с концентрационными значениями диаграммы состояния Fe – N. При этом равновесие на этой границе с течением времени практически не изменяется при любой технологии азотирования (Рисунок 2). Последующий рост α-твердого раствора и γꞌ фазы подчиняется параболической закономерности.
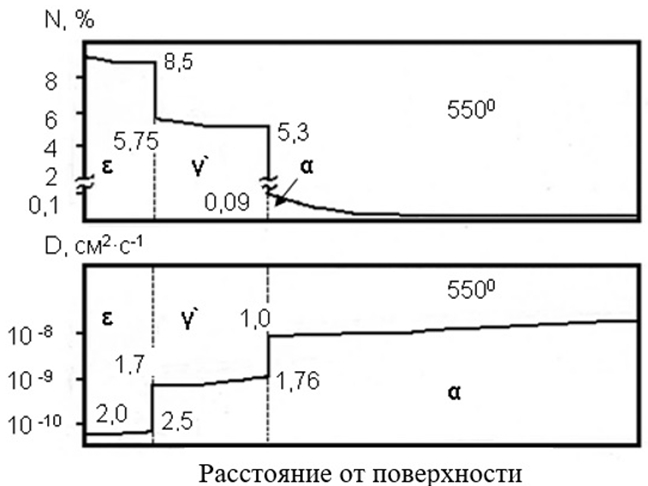
Рис. 2 – Концентрационное распределение азота на границах раздела фаз азотированного слоя и значения коэффициентов диффузии в фазах при 550 0С
Принимая во внимание не изменяющийся характер концентрации азота на границах раздела фаз для описания кинетики их роста нами предложена экспериментальная характеристика, названная кинетическим коэффициентом (D), который находится из выражения параболической закономерности роста фаз:
где y – толщина конкретной фазы азотированного слоя; τ – продолжительность процесса, D – кинетический коэффициент.
По нашему мнению, этот кинетический коэффициент (D), который в ряде работ называется эффективным коэффициентом диффузии [4], [6], интегрально и косвенно отражает совокупность следующих процессов и характеристик:
- процессы, протекающие в среде обработки и степень стабильности реакций массопереноса;
- процессы, протекающие на поверхности обрабатываемого металла и ее реакционную способность в конкретной среде;
- структурное состояние металла основы и его фазовый состав;
- коэффициент диффузии и свойства взаимодействующих элементов (атомные радиусы, кристаллические решетки, тип взаимодействия и т.п.).
На основании проведенных экспериментов по азотированию технического железа в различных средах были получены значения кинетических коэффициентов роста фаз при технологически обоснованной продолжительности, которые с учетом температурной зависимости приведены к единым температурным условиям (Таблица 1).
Все эксперименты проводились при температурах 500 – 590℃, продолжительность процессов была выбрана с учетом получения технологически приемлемой толщины покрытия. Исследование изменений кинетического коэффициента в зависимости от температуры проведения азотирования позволили аппроксимировать полученные зависимости и рассчитать приведенные значения.
Таблица 1 – Значения приведенных кинетических коэффициентов роста фаз азотированных слоев в различных средах
| № п/п | Вид процесса насыщения | Время обработки, ч | Приведенный кинетический коэффициент D_(ε+γꞌ)^500 | Приведенный кинетический коэффициент D_α^500 |
| 1 | Расплавы солей цианатов Na и K | 1,5 | 7,0 | 500 |
| 2 | Газобарический процесс (герметизированные контейнеры) | 1,5 | 3,0 | 285 |
| 3 | Газовое ионное азотирование в аммиачной среде | 4 | 7,0 | 275 |
| 4 | Насыщение из порошковых смесей | 4 | 3,0 | 260 |
| 5 | Насыщение из газовой аммиачной среды (NH3+N2+H2) | 5 | 7,0 | 235 |
где Кα = 0,2281e0,0029Т;
![]() (3)
(3)
где Кγ'+ε = 0,0059e0,0102Т; Т - задаваемая температура, ℃.
Расчет кинетического коэффициента для слоя нитридов проводился без разделения γꞌ и ε фаз. Таким образом, имея приведенное значение кинетического коэффициента можно рассчитать его величину при других температурах в исследованном интервале.
Важным моментом моделирования кинетического коэффициента является степень его изменения от продолжительности обработки. То есть закономерность роста фаз слоя полностью не подчиняется параболической зависимости (√τ), вследствие сложности процессов на границах фаз, а для α-твердого раствора дополнительно связана с дисперсным выделением нитридов, требующих для своего образования некоторого количества атомов азота. Наиболее удобным, по нашему мнению, эту степень снижения кинетического коэффициента выразить в процентах (%) по отношению к его приведенному значению, а поправку в модель вводить после расчета толщины фаз слоя по параболической зависимости. В данном случае процентное снижение коэффициента во времени не зависит ни от марки стали, ни от технологических составов конкретного процесса.
В частности, при увеличении продолжительности процесса кинетический коэффициент для α – твердого раствора снижается в большей степени в жидкой среде, в которой его значение выше, и в меньшей степени - для газовых процессов. Отсюда вытекает и технологическая продолжительность азотирования в рассматриваемых средах. Аппроксимация зависимостей изменения кинетического коэффициента роста α-слоя от продолжительности процесса (в %) при температурах <590℃ при азотировании технического железа в разных средах привела к следующим формулам (4 - 6):
- при ионном азотировании –
где R2 – достоверность аппроксимации;
τ– продолжительность азотирования.
Поскольку азотированию подвергают всевозможные конструкционные стали с различным содержанием углерода и легирующих элементов, поэтому следующим этапом работы явилось исследование влияния легирующих элементов на толщину азотированного слоя. Для этого использовались как стандартные конструкционные стали, так и специально выплавленные сплавы с переменным содержанием одного из легирующих элементов.
Анализ полученных результатов и аппроксимация зависимостей привели к получению формул влияния процентного содержания легирующих элементов на толщины фаз азотированного слоя (Таблицы 2, 3). Расчет толщины для слоя нитридов проводился без разделения γꞌ и ε фаз.
Таблица 2 – Расчетные формулы влияния содержания легирующих элементов на толщину слоя нитридов γ' + ɛ.
| № п/п | Легирующий элемент | Формула влияния |
| 1 | Mn | yε + γ' = 0,2215x2 - 2,4494x + 42,343 |
| 2 | Ni | yε + γ' = 0,6866x2 - 8,0185x + 41,605 |
| 3 | Cr | yε + γ' = 0,4203x2 - 4,5995x + 41,741 |
| 4 | Mo | yε + γ' = 0,8375x2 - 9,8022x + 40,642 |
| 5 | W | yε + γ' = 2,4685x2 - 19,551x + 42,174 |
| 6 | Cu | yε + γ' = 30,105x3 - 74,85x2 + 38,462x + 42,141 |
| 7 | Zn | yε + γ' = 0,2538x3 - 2,2727x2 + 1,4662x + 42,361 |
| 8 | Zr (Nb) | yε + γ' = 0,6563x2 - 9,2641x + 41,412 |
| 9 | V | yε + γ' = 0,098x4 - 1,4711x3 + 8,2607x2 - 23,699x + 41,662 |
| 10 | Ti | yε + γ' = 0,1442x2 - 2,3697x + 42,099 |
| 11 | Al | yε + γ' = –0,1774x3 + 2,0755x2 - 8,6316x + 41,057 |
| 12 | C | yε + γ' = –0,112x3 + 1,9455x2 - 12,465x + 41,857 |
Расчет толщины слоя при содержании нескольких легирующих элементов проводится либо путем последовательного учета влияния каждого элемента (K_i^(л.э.) ),либо одновременным расчетом.
Общая формула расчета имеет вид:
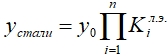 (7)
где
(7)
где 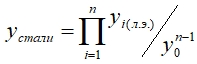 (8)
(8)
где у0 – толщина слоя на железе, определенная либо путем решения уравнений Фика, либо экспериментальным путем из результатов в определенных условиях и получением приведенного кинетического коэффициента;
n - число легирующих элементов в стали; i = 1, 2, 3, ……., n.
Таблица 3 – Расчетные формулы влияния содержания легирующих элементов на толщину α – слоя
| № п/п | Легирующий элемент | Формула влияния |
| 1 | Si | yα = - 0.2727x3 + 6.2541x2 - 57.321x + 606.52 |
| 2 | Cr (Nb) | yα= 0.1779x4 - 2.5888x3 + 16.366x2 - 94.511x + 609.62 |
| 3 | Mn | yα = - 0.4476x3 + 9.2311x2 - 75.152x + 603.39 |
| 4 | Mo | yα= 4.5877x4 - 43.175x3 + 146.9x2 - 277.55x + 605.33 |
| 5 | W | yα = 126.81x6 - 959.01x5 + 2758.5x4 - 3775.4x3 + 2535.8x2 - 915.24x + 602.96 |
| 6 | C | yα= 1.925x4 - 27.808x3 + 141.31x2 - 321.75x + 603.18 |
| 7 | Al | yα= - 1.0153x5 + 17.481x4 - 112.32x3 + 335.94x2 - 500.05x + 607.45 |
| 8 | V | yα= 0.2189x4 - 3.176x3 + 19.399x2 - 102.34x + 609.12 |
| 9 | Ti (Zr) | yα= -1.026x5 + 17.813x4 - 115.63x3 + 350.11x2 - 525.51x + 607.36 |
| 10 | Cu (Zn) | yα = - 0.2746x3 + 3.91x2 - 52.012x + 609.7 |
| 11 | Ni | yα = 0.9724x4 - 13.808x3 + 68.541x2 - 157.3x + 605.79 |
| 12 | S | yα= - 0.338x3 + 3.8942x2 - 28.897x + 607.25 |
| 13 | P | yα = - 0.3397x3 + 4.3806x2 - 40.739x + 607.25 |
Результаты и обсуждения
В работе экспериментально установлена последовательность образования фаз азотированного слоя и показано, что образование на поверхности сплошного слоя последующей фазы тормозит рост предыдущей фазы. Этот факт играет существенную роль при кратковременной обработке. При длительных выдержках он нивелируется.
Принимая во внимание закономерности образования фаз слоя и граничные концентрации азота было сделано заключение об общности формирования фаз при любых технологических вариантах азотирования, что не нарушает физики процесса и позволяет прийти к разработке общей модели расчета. При этом учет особенностей разных технологий азотирования проводился путем использования приведенного кинетического коэффициента, который интегрально и косвенно отражает процессы в насыщающем пространстве, процессы на обрабатываемой поверхности и диффузионные процессы в обрабатываемом металле. Установленная закономерность изменения кинетического коэффициента от температуры и продолжительности обработки позволила проводить расчеты при любых значениях условий в рамках исследованных параметров. В конечном итоге это обеспечило повышение достоверности расчетных значений толщин фаз азотированных слоев.
В результате проведенных экспериментов, сравнения полученных результатов с расчетными и логических рассуждений сделано заключение, что наличие легирующих элементов оказывает одинаковое влияние на толщины слоя нитридов и α – твердого раствора при различных условиях протекания процесса. То есть на диффузионные процессы в твердом теле внешняя среда влияет только значением концентрации азота на поверхности, активируя тем самым процесс встречной диффузии элементов материала основы, имеющих большое сродство к азоту. А это влияние уже учтено кинетическим коэффициентом. То есть предлагаемые формулы по влиянию легирующих элементов на толщины фаз слоя в соответствии с принципом подобия [9] применимы при расчете толщин слоев для любых технологических вариантов проведения процесса азотирования. Это стало возможным только при использовании приведенного кинетического коэффициента для каждого вида обработки.
При расчете толщины слоя нитридов и α – твердого раствора в зависимости от процентного содержания легирующих элементов было показано, что ошибка расчетных величин по отношению к экспериментальным составляет не более 9 %, что меньше, даже разницы расчетных и экспериментальных данных, вносимых колебаниями химического состава в обрабатываемых сталях (Таблица 4).
Таблица 4 – Достоверность расчетных результатов
| Марка стали | Толщина α-слоя экспериментальная, мкм | Толщина α-слоя расчетная, мкм | Погрешность, % |
| 10 | 650 | 620 | 4,6 |
| 35 | 550 | 528 | 4,0 |
| 80 | 500 | 520 | 4,0 |
| 35ХГМ | 400 | 430 | 7,5 |
| 30Х2МНЮА | 400 | 414 | 3,5 |
| 25ГФС | 480 | 471 | 1,9 |
| 40Х5МФС | 160 | 157 | 1,8 |
| Х | 400 | 430 | 7,5 |
| 30Х3М | 385 | 350 | 9,2 |
| 35Х2Н4М | 350 | 325 | 7,1 |
| 35ХГН2 | 400 | 419 | 4,7 |
| А45Г2 | 500 | 481 | 3,8 |
| АС15Г | 650 | 620 | 4,6 |
Контрольные эксперименты (соляная ванна, содержащая 38 % CNO-, 570° C; 1,5 ч.) и расчет толщины слоя α – твердого раствора проводился по среднему содержанию легирующих элементов в сталях, в соответствии со справочными данными. Рассчитанная толщина α – твердого раствора не только определяет эффективность технологического процесса азотирования, но и может успешно применяться для расчета распределения азота в слое и расчета твердости [10].
Заключение
Результатом данной работы явилось создание математической модели расчета толщин фаз азотированного слоя, в том числе при наличии в стали легирующих элементов, обеспечивающая более высокую достоверность по сравнению с ранее разработанными методиками. Важным этапом работы является экспериментальное определение порядка образования фаз азотированного слоя и определение величин кинетических коэффициентов при различных способах насыщения. Эти кинетические коэффициенты интегрально связывают процессы, протекающие в насыщающей среде, на обрабатываемой поверхности и в обрабатываемом материале.
При расчете толщины азотированного слоя в зависимости от процентного содержания легирующих элементов, ошибка расчетной величины по отношению к экспериментальной составляет не более 9%, что меньше, чем влияние колебания химического состава в обрабатываемых сплавах на толщину слоя, и является приемлемым для осуществления предварительного расчета.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Лахтин Ю.М. Химико-термическая обработка металлов / Ю.М. Лахтин, Б.Н. Арзамасов – М.: Металлургия, 1985. – 256 c.
- Лахтин Ю.М. Теория и технология азотирования / Ю.М. Лахтин, Я.Д. Коган, Х.Й. Шпис и др. – М.: Металлургия, 1991. – 320 c.
- Mittemeijer E.J. Thermodynamics, kinetics and process control of nitriding. / E.J. Mittemeijer, M.A.J Somers // Surface Engineering. – 1997. – 13. – p. 483-497.
- Torchan L. Control of nitride layers growth kinetics in the binary Fe-N system. / L. Torchan, P. Bilger, J. Dulcy et al. // Metall. . – 1996. – 27. – p. 1823-1835.
- Torchan L., Bilger P., Dulcy J., Gantois M. “Application of a mathematical model of iron nitride layer growth during gas phase nitriding”. Proceeding of the Second ASM Heat Treatment and Surface Engineering. Dortmund (Germany), 1-3 June 1993
- Ratajski J. Model of growth kinetics of nitride layers in the binary Fe – N system. //Nitriding technology. Proceedings the 9th international seminar. Warsaw, Poland 2003. P. 149-159.
- Крукович М.Г. Моделирование процесса азотирования. / М.Г. Крукович // МиТОМ. – 2004. – 1. – c. 24-31.
- Зинченко В.М. Азотный потенциал / В.М. Зинченко, В.Я. Сыропятов, Б.А. Прусаков и др. – М.: Машиностроение, 2003. – 71 c.
- Крукович М.Г. Применение принципа подобия при моделировании кинетики роста азотированных слоев на сталях. / М.Г. Крукович, А.Д. Федотова // Новые материалы и технологии в машиностроении. – 2019. – 30. – c. 55-60.
- Крукович М.Г. Эмпирическое моделирование распределения твердости α - твердого раствора азотированного слоя. / М.Г. Крукович, А.Д. Федотова // Международный научно-исследовательский журнал. – 2020. – 12-1 (102). – 38-42.
Список литературы на английском языке / References in English
- Laxtin Yu.M. Ximiko-termicheskaya obrabotka metallov [Chemical heat treatment of metals] / Yu.M. Laxtin, N. Arzamasov – M.: Metallurgiya, 1985. – 256 p. [in Russian]
- Laxtin Yu.M. Teoriya i texnologiya azotirovaniya [Theory and technology of nitriding] / Yu.M. Laxtin, Ya.D. Kogan, X.J. Shpis et al. – M.: Metallurgiya, 1991. – 320 p. [in Russian]
- Mittemeijer E.J. Thermodynamics, kinetics and process control of nitriding. / E.J. Mittemeijer, M.A.J Somers // Surface Engineering. – 1997. – 13. – p. 483-497.
- Torchan L. Control of nitride layers growth kinetics in the binary Fe-N system. / L. Torchan, P. Bilger, J. Dulcy et al. // Metall. . – 1996. – 27. – p. 1823-1835.
- Torchan L., Bilger P., Dulcy J., Gantois M. “Application of a mathematical model of iron nitride layer growth during gas phase nitriding”. Proceeding of the Second ASM Heat Treatment and Surface Engineering. Dortmund (Germany), 1-3 June 1993
- Ratajski J. Model of growth kinetics of nitride layers in the binary Fe – N system. //Nitriding technology. Proceedings the 9th international seminar. Warsaw, Poland 2003. P. 149-159.
- Krukovich M.G. Modelirovanie processa azotirovaniya [Modeling the nitriding process]. / M.G. Krukovich // MiTOM [MiTOM]. – 2004. – 1. – p. 24-31. [in Russian]
- Zinchenko V.M. Azotny'j potencial [Nitrogen potential] / V.M. Zinchenko, V.Ya. Sy'ropyatov, B.A. Prusakov et al. – M.: Mashinostroenie, 2003. – 71 p. [in Russian]
- Krukovich M.G. Primenenie principa podobiya pri modelirovanii kinetiki rosta azotirovanny'x sloev na stalyax [Application of the principle of similarity in modeling the kinetics of growth of nitrided layers on steels]. / M.G. Krukovich, A.D. Fedotova // Novy'e materialy' i texnologii v mashinostroenii [New materials and technologies in mechanical engineering]. – 2019. – 30. – p. 55-60. [in Russian]
- Krukovich M.G. E'mpiricheskoe modelirovanie raspredeleniya tverdosti α - tverdogo rastvora azotirovannogo sloya [Empirical modeling of hardness distribution of α - solid solution of a nitrided layer]. / M.G. Krukovich, A.D. Fedotova // Mezhdunarodny'j nauchno-issledovatel'skij zhurnal [International research journal]. – 2020. – 12-1 (102). – p. 38-42. [in Russian]