Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

МОДЕЛИРОВАНИЕ ПСИХОЛОГО-ПЕДАГОГИЧЕСКИХ ПОРТРЕТОВ ПРЕПОДАВАТЕЛЕЙ И ОБУЧАЕМЫХ

Научная статья
Ганичева А.В.
Ганичев А.В.
DOI:
https://doi.org/10.23670/IRJ.2021.114.12.189
Выпуск: № 12 (114), 2021
PDF

Моделирование психолого-педагогических портретов преподавателей и обучаемых

Научная статья

Ганичева А.В.1, Ганичев А.В.2,*

1ORCID: 0000-0002-0224-8945;

2 ORCID: 0000-0003-3389-7582;

1 Тверская государственная сельскохозяйственная академия, Тверь, Россия;

2 Тверской государственный технический университет, Тверь, Россия,

* Корреспондирующий автор (alexej.ganichev[at]yandex.ru)

Аннотация

Внедрение цифровых методов в образовательный процесс делает актуальным использование математических методов и моделей. Важной проблемой является математическое описание характеристик обучаемых и преподавателей, которые образуют их психолого-педагогические портреты. В качестве моделей портретов выбраны их векторные характеристики и матричное представление. Для математического согласования цифровых портретов при векторном описании предлагается применять величину их скалярного произведения. Разработан метод, позволяющий найти пропорции элементов структурной матрицы портретов, при которых будут сбалансированы характеристики преподавателей и обучаемых в данном учебном коллективе. Метод основан на анализе значения собственного числа структурной матрицы модели.

Ключевые слова: эксперт, векторный портрет, скалярное произведение, структурная матрица, вектор, собственное число матрицы.

Modeling of Psychological and Pedagogical Portraits of Teachers and Students

Research article

Ganicheva A.V.1,Ganichev A.V.2,*

1 ORCID: 0000-0002-0224-8945;

2 ORCID: 0000-0003-3389-7582;

1Tver State Agricultural Academy, Tver, Russia;

2Tver State Technical University, Tver, Russia

* Corresponding author (alexej.ganichev[at]yandex.ru)

Abstract

The introduction of digital methods into the educational process makes the use of mathematical methods and models relevant. The mathematical description of the characteristics of students and teachers who form their psychological and pedagogical portraits is an important problem. Their vector characteristics and matrix representation are chosen as portrait models. For mathematical matching of digital portraits with vector description, it is proposed to apply the magnitude of their scalar product. The article introduces a method of finding the proportions of the elements of the structural matrix of portraits, in which the characteristics of teachers and students in this educational team will be balanced. The method is based on the analysis of the eigenvalue of the structural matrix of the model.

Keywords: expert, vector portrait, scalar product, structural matrix, vector, matrix eigenvalue.

Введение

Проблема составления психологических портретов является очень важной во многих сферах жизни общества. Эта проблема является очень актуальной для учебных заведений. В учебных заведениях для разработки психологических портретов обучаемых и психолого-педагогических портретов преподавателей используют в настоящее время преимущественно два метода: тестирование и анкетирование. Следует отметить, что заполнять и обрабатывать анкеты и тесты вручную крайне трудоемко и неэффективно. Программные продукты используют для обработки результатов этих анкетирования и тестирования, при этом применяются, в основном, статистические методы. Использование для решения данной проблемы преимущественно мнения экспертов-психологов вносит в формируемые портреты элемент субъективизма, а это может быть и предвзятость суждений. Поэтому разработка новых методов автоматизации процессов создания психологических портретов является важной и актуальной задачей.

Для повышения эффективности учебного процесса следует учитывать при его планировании, организации и управлении особенности и характерные качества, как преподавателей, так и типологию личности обучаемых.

Важнейшие черты современных студентов (ответственность, мотивация к процессу, результату обучения, успеху), полученные методом тестирования, рассмотрены в статье [1]. В работе [2] приведены социально-психологический портреты современного студенчества, полученный методом анкетирования. Психолого-педагогический, социально-типический портреты современного преподавателя ВУЗа представлены, соответственно, в статьях [3], [4]. Инструментарий составления портретов – анкетирование и опрос. Интересным вопросом является представление студентов о современном преподавателе вуза [5], в том числе о идеальном преподавателе [6]. Рассматриваются личностные качества и социально-профессиональные компетенции. Важной проблемой является организация взаимодействия участников образовательного процесса для повышения эффективности подготовки студентов [7]. Для решения данной проблемы следует построить математические модели согласования основных качеств субъектов учебного процесса. В работе [8] предложен метод количественной оценки качеств преподавателей и обучаемых с помощью теории нечетких множеств. В статье [9] разработана модель согласования портретов преподавателей и обучаемых. В [10] для определения степени согласования интересов индивидуумов используется аппарат теории формальных грамматик, а в [11] ‑ методы теории многоуровневых иерархических систем.

Данные о численной оценке качеств преподавателей и студентов, наиболее значимых для их эффективного взаимодействия, приведены в работе [12]. Эти данные получены на основе анкетирования 408 студентов и 144 преподавателей и аспирантов региональных вузов.

Большое внимание взаимодействию преподавателей и обучаемых уделяется за рубежом. Эта область исследований считается новой, важной и относительно мало исследованной [13]. Обзор основных проблем и достижений зарубежных ученых по данной проблеме изложен в работе [14]. Особенности и роль личности преподавателя в образовательном процессе рассмотрены в исследовании [15].

Количественные оценки взаимодействия преподавателей и обучаемых в разнообразных условиях динамичного учебного процесса могут быть получены методом математического моделирования, но в настоящее время эта проблема еще недостаточно изучена.

Целью данной работы является разработка методов и моделей согласования портретов преподавателей и обучаемых. Для решения этой задачи применяется аппарат векторного описания характеристик портрета и его матричное представление.

Методы и принципы исследования

  1. Векторные характеристики портрета

Можно выделить основные качества преподавателей: компетентность, умение объяснять материал, честность, объективность, трудолюбие, культура общения и т.д. К характеристикам обучаемых относятся: интеллектуальность, эрудированность, креативность, трудолюбие, дисциплинированность, способность к самооценке и т.д.

Качества преподавателей и обучаемых оцениваются путем тестирования, анкетирования, оценок экспертов. В роли экспертов выступают преподаватели, обучающиеся, психологическая служба, руководство учебной организации.

С помощью метода экспертных оценок формируются коллективные оценки качеств преподавателей (П) и учащихся (У).

В соответствии с определенными шкалами согласно вопросам анкетирования данного П с учетом мнения данного У и аналогично анкетирования данного У с учетом мнения данного П составляются векторы  и . Координаты  представляют собой численное выражение (оценку) качеств данного П данным У. Аналогично вектор  дает численную оценку качеств данного У в восприятии данного П.

Векторные портреты П и У можно сравнивать с эталонными портретами (векторами нормы). Координаты этих векторов рассматриваются,например, как средние арифметические мнения всех учащихся и сотрудников данного учебного заведения относительно того, как они оценивают качества П и У. В качестве эталонных координат можно также полагать максимальные значения шкалы оценивания. В случае совпадения длин векторов важную роль играет отклонение вектора от эталона. В этом случае сравниваются скалярные произведения одного и другого вектора с эталоном.

Пусть  и ‑ соответствующие векторы нормы. Сравнивая скалярные произведения  для разных i, можно судить о качестве портрета : чем больше скалярное произведение, тем выше качество портрета.

Если характеристики, включаемые в портрет, неравноправны между собой, то их численные оценки могут браться с соответствующими весовыми коэффициентами.

Возможен следующий подход. Если данное качество П плохо действует на данногоУ, то соответствующая координата в векторе зануляется. Аналогично для вектора  Если j-ая координата соответствует качествам П и У, которые одновременно плохо действуют друг на друга, то произведение координат при формировании скалярного произведения берется со знаком «-». Тогда целесообразно считать более качественным портрет с большим скалярным произведением.

Векторные портреты  и  связаны с процессом получения и усвоения учебных фрагментов e данной дисциплины. Поэтому рассматриваются векторы  и .

В общем случае координаты векторов  и  меняются со временем, в частности, при переходе от одного изучаемого фрагмента к другому, т.е. и . Фиксируя моменты перехода к изучению следующего учебного фрагмента дисциплины, для П иУ получаем сетевые графики, узлы которых представляют собой точки  и  в моменты времени , дуги соответствуют изучаемому учебному фрагменту. Нагрузке по дуге соответствует, например, время изучения данного фрагмента данным учащимся, либо балл, полученный при изучении данного фрагмента.

Такое представление динамического портрета качеств П и У дает возможность изменять оценки этих качеств в соответствии с правилами расчета сетевого графика, а также определения пропускной способности транспортной сети.

Одной из важных задач организации учебного процесса является создание благоприятного микроклимата в учебной группе с точки зрения согласования портретов преподавателя и учащихся. В качестве меры согласованности портретов могут использоваться разные критерии, например: линейное отклонение координат портрета, косинус угла между векторами, Евклидово расстояние между портретами и другие меры расстояния.

  1. Матричная модель портрета

По аналогии с линейной моделью обмена [16, С. 90] предлагается следующая матричная модель согласования портрета преподавателя и учащихся. В портрет включим n характеристик, имеющих веса (x1, x2,…,xn). Cтруктурная матрица согласования портретов имеет вид:

1 A– структурная матрица, ‑ собственное число матрицы, ‑ искомый вектор.

От матричного уравнения переходим к системе линейных уравнений, которая решается, например, методом Гаусса. Получаем пропорции характеристик.

Заметим, что матрица A должна быть квадратной. Если это не так, вводим дополнительные качества (может быть, фиктивные, т.е. нулевые элементы структурной матрицы) или дополнительных учащихся (может быть, фиктивных, с нулевыми координатами в структурной матрице).

Полученные отношения по согласованию портретов следует учитывать при организации и проведении учебного процесса.

Основные результаты

Рассмотрим примеры. К качествам преподавателей и студентов, значимых для эффективного взаимодействия, в работе [12] отнесено 32 характеристики. Выберем среди них пять: объективность, доброжелательность, эрудиция, добросовестность, требовательность. Для этих характеристик на основе данных, приведенных в [4], векторы средних значений (по 10-балльной шкале) равны 1. Следовательно, имеем векторные портреты П и У. При этом, чем большие значения принимают координаты вектора, тем качественнее портрет. Портреты можно сравнивать по значению модуля вектора. Так, для рассматриваемого примера 1.

Проанализируем следующий пример. По оценкам студентов получены портреты двух преподавателей: 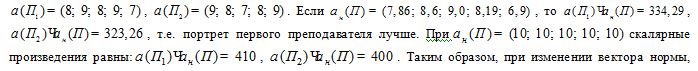1ранжирование портретов не меняется.

Аналогичные рассуждения и выводы справедливы также для a(Yt).

Обобщенный портрет для данных П и У можно охарактеризовать скалярным произведением a(П) Ча (У) при использования портретов для координат  а (П) и а(У).

Для примера: 1

Метод решения задачи согласования портрета преподавателя и рассмотрим на следующем примере. Пусть имеется четыре учащихся. В портрет включим четыре характеристики: объективность (B1), добросовестность (B2), внимательность (B3), самокритика(B4). По данным работы [12] черты преподавателя 1 . Пусть для примера, портреты четырех учащихся имеют вид: 1 1

Построим структурную матрицу согласования портретов преподавателя и учащихся. Для этого используем абсолютную величину разности между вектором преподавателя и векторами учащихся. А именно: первый столбец 1 т.е.

1

Первый столбец показывает степень согласования характеристик учащегосяУ1 с характеристиками преподавателя: в 1-ой строке–с характеристикой B1, во 2-ой строке– сB2, в 3-ей– B3, в 4-ой– B4; второй столбец отражает степень согласования характеристик учащегося У2 с соответствующими характеристикамиB1, B2,B3, B4 преподавателя и т.д.

В результате согласования характеристика преподавателя Bi получает некоторый выигрыш 1, который равен 1, где  – элемент структурной матрицы. Переменные xi могут иметь разное смысловое содержание. В ВУЗе это может быть выигрыш по баллам, рейтингу или времени усвоения материала учащимися. Может рассчитываться комплексный показатель выигрыша. Этот выигрыш учитывается при планировании учебной, методической, научной, воспитательной работы.

Требуется определить пропорции (x1, x2, x3, x4), при которых собственное число матрицы А будет равно 1. В этом случае будут сбалансированы характеристики в учебной группе.

Алгоритм решения задачи следующий:

1) записывается основное матричное уравнение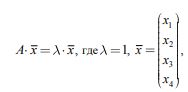1

A– структурная матрица, л‑ собственное число матрицы, х ‑ искомый вектор.

От матричного уравнения переходим к системе:

1

2) решая систему линейных уравнений, например, методом Гаусса, получим:

1

где c – положительное действительное число.

Если искомый вектор х будет содержать нулевые или отрицательные координаты, то это означает, что при исходных данных не удается сбалансировать проявление рассматриваемых характеристик у данных учащихся.

Таким образом, в данной учебной группе возможно согласование портретов. Оно получается для вектора 1 . Полученный результат означает, что проявление четырех характеристик должно соответствовать отношениям 1переходя к целым числам, получаем, что 1, как 140:160:105:200, т.е. при работе с данными четырьмя учащимися наибольший результат связан с характеристикой преподавателя B4, наименьший – с B1.

Заключение

Расчет оптимального соотношения качеств участников учебного процесса позволяет определить степень согласования их интересов в группе и определить пути ее увеличения. Это позволит улучшить качество процесса обучения за счет ликвидации или сглаживания конфликтных ситуаций, оптимального распределения часов лекций и практических занятий, определения сроков проведения контрольных мероприятий, формирования индивидуальных траекторий обучения студентов.

Разработанные методы и модели могут быть использованы не только в образовательном процессе, но и при формировании различных коллективов – исполнителей совместной работы в любых сферах деятельности. Это могут быть организационно-управленческие, производственные, научные, творческие коллективы.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Булатова Д.С. Современный студент технического вуза: элементы психологического портрета / Д.С. Булатова, А.А. Казбекова, Я.Л. Либерман // Педагогическое образование в России. ‑ 2016. ‑ № ‑ С. 87-92.
  2. Грязнов А.Н. Социально-психологический портрет студента / А.Н. Грязнов, В.Ш. Масленникова, В.А. Боговарова // Казанский педагогический журнал. ‑ 2013. – № 3 (98). – С. 160-167.
  3. Загороднюк А.Н. Психолого-педагогический портрет современного преподавателя ВУЗа / А.Н. Загороднюк // Kant. ‑ 2018. ‑ № 4 (29). ‑ С. 26-30.
  4. Лапшов В.А. Социально-типический портрет преподавателя отечественного вуза / В.А. Лапшов // Социология образования. ‑ 2016. ‑ № 4. ‑ С. 4-14.
  5. Андреева Э.В. Современный преподаватель вуза глазами студентов / Э.В. Андреева // Аллея науки. ‑ 2018. ‑ № 4 (20). ‑ С. 874-876.
  6. Ефимова Г.З. Идеальный педагог высшей школы: личностные качества и социально-профессиональные компетенции / Г.З. Ефимова, А.Н. Сорокин, М.В. Грибовский // Образование и наука. ‑ 2021. ‑ Т. 23. ‑ № 1. ‑ С. 202-230. ‑DOI: 10.17853/1994-56392021-1-202-230.
  7. Анциферова А.Г. Взаимодействие преподавателя и студента как фактор воздействия на личностный и профессиональный рост обучающегося / А.Г. Анциферова // Электронный научно-методический журнал Омского ГАУ. ‑ 2016. ‑ № 3 (6). ‑ С. 23.
  8. Ганичева А.В. Оценка психолого-педагогических портретов преподавателей и обучаемых / А.В. Ганичева // Экономические и гуманитарные исследования регионов. ‑ 2018. ‑ № ‑ С. 30-33.
  9. Ганичева А.В.Математическая модель взаимоотношений индивидуумов / А.В. Ганичева, А.В. Ганичев // Научное обозрение. Международный научно-практический журнал. ‑ 2018. ‑ № 3. ‑ С. 4.
  10. Ганичева А.В. Модель согласования портретов преподавателей и обучаемых / А.В. Ганичева, А.В. Ганичев // Моделирование, оптимизация и информационные технологии. ‑ 2020. ‑ Т. 8. ‑ № 3 (30). ‑ С. 16-17.
  11. Ганичева А.В. Согласование интересов участников учебного процесса / А.В. Ганичева // Бизнес. Образование. Право. ‑ 2017. ‑ № 4 (41). ‑ С. 350-355.
  12. Макарова Л.Н. Проблемные зоны взаимодействия преподавателей и студентов / Л.Н. Макарова, М.В. Старцев // Социально-экономические явления и процессы. ‑ 2017. ‑ Т. 12. ‑ № 5. ‑ С. 210-216.
  13. Göncz A. The influence of students’personality traits on their perceptionof a good teacher within the five-factor model of personality /A.Göncz, L.Göncz, J. Pekić // Acta Polytechnica Hungarica. 2014; 11: 65–86. DOI:10.12700/APH.11.03.2014.03.5.
  14. Göncz L. Teacher personality: a review of psychological researched guidelines for a more comprehensive theory in educational psychology /Göncz// Open Review of Educational Research. 2017; 4(1): 75-95. DOI: 10.1080/23265507.2017.1339572.
  15. Romanov D.K. Psychological aspects of perception and understandings of teachers by university students / K. Romanov, L.M. Dauksha // Integration of Education. 2016; 2(20): 228-237. DOI: 10.15507/1991-9468.083.020.201602.228-237.
  16. Высшая математика для экономистов / [Н.Ш. Кремер и др.]; под ред. проф. Ш.  Кремера. - 3-е изд. - М.: ЮНИТИ-ДАНА, 2010. -479 с.

Список литературы на английском языке / References in English

  1. Bulatova D.S. Sovremennyjj student tekhnicheskogo vuza: ehlementy psikhologicheskogo portreta [A modern student of a technical university: elements of a psychological portrait] / D. S. Bulatova, A. A. Kazbekova, Ya. L. Liberman // Pedagogicheskoe obrazovanie v Rossii [Pedagogical education in Russia]. ‑ 2016. ‑No. 4. ‑pp. 87-92 [in Russian]
  2. Gryaznov A.N. Social'no-psikhologicheskijj portret studenta [Socio-psychological portrait of a student] / A. N. Gryaznov, V. Sh. Maslennikova, V. A. Bogovarova // Kazanskijj pedagogicheskijj zhurnal [Kazan Pedagogical Journal]. ‑2013. – № 3 (98). – pp. 160-167 [in Russian]
  3. Zagorodnyuk A.N. Psikhologo-pedagogicheskijj portret sovremennogo prepodavatelja VUZa [Psychological and pedagogical portrait of a modern university teacher] / A. N. Zagorodnyuk // Kant. ‑2018. ‑No. 4 (29). ‑pp. 26-30 [in Russian]
  4. Lapshov V.A. Social'no-tipicheskijj portret prepodavatelja otechestvennogo vuza [Socio-typical portrait of a teacher of a domestic university // Sociology of education] / V. A. Lapshov. ‑ 2016. ‑No. 4. ‑pp. 4-14 [in Russian]
  5. Andreeva E.V. Sovremennyjj prepodavatel' vuza glazami studentov [A modern university teacher through the eyes of students] / E. V. Andreeva // Alleya nauki [Alley of Science]. ‑2018. ‑No. 4 (20). ‑pp. 874-876 [in Russian]
  6. Efimova G.Z. Ideal'nyjj pedagog vysshejj shkoly: lichnostnye kachestva i social'no-professional'nye kompetencii [The ideal teacher of a higher school: personal qualities and socio-professional competencies] / G. Z. Efimova, A. N. Sorokin, V. Gribovsky // Obrazovanie i nauka [Education and Science]. ‑ 2021. ‑Vol. 23. ‑No. 1. ‑pp. 202-230. ‑DOI: 10.17853/1994-56392021-1-202-230 [in Russian]
  7. Antsiferova A.G. Vzaimodejjstvie prepodavatelja i studenta kak faktor vozdejjstvija na lichnostnyjj i professional'nyjj rost obuchajushhegosja [Interaction of a teacher and a student as a factor of influence on the personal and professional growth of a student] / A. G. Antsiferova // Ehlektronnyjj nauchno-metodicheskijj zhurnal Omskogo GAU[Electronic scientific and methodological journal of the Omsk State Agrarian University]. ‑ 2016. ‑No. 3 (6). ‑p. 23[in Russian]
  8. Ganicheva A.V. Ocenka psikhologo-pedagogicheskikh portretov prepodavatelejj i obuchaemykh [Evaluation of psychological and pedagogical portraits of teachers and trainees] / A. V. Ganicheva // Ehkonomicheskie i gumanitarnye issledovanija regionov [Economic and humanitarian studies of the regions]. ‑ 2018. ‑ № 5. ‑pp. 30-33 [in Russian]
  9. Ganicheva A.V. Matematicheskaja model' vzaimootnoshenijj individuumov [Mathematical model of the relationship of individuals] / A. V. Ganicheva, A. V. Ganicheva // Nauchnoe obozrenie. Mezhdunarodnyjj nauchno-prakticheskijj zhurnal [Scientific review. International Scientific and Practical journal]. ‑2018. ‑No. 3. ‑p. 4 [in Russian]
  10. Ganicheva A.V. Model' soglasovanija portretov prepodavatelejj i obuchaemykh [Model of matching portraits of teachers and trainees] / A. V. Ganicheva, A. V. Ganicheva // Modelirovanie, optimizacija i informacionnye tekhnologii [Modeling, optimization and information technologies]. ‑ 2020. ‑Vol. 8. ‑No. 3 (30). ‑pp. 16-17 [in Russian]
  11. Ganicheva A.V. Soglasovanie interesov uchastnikov uchebnogo processa [Coordination of interests of participants in the educational process] / A. V. Ganicheva // Biznes. Obrazovanie. Pravo. [Business. Education. Law]. ‑2017. ‑No. 4 (41). ‑ 350-355 [in Russian]
  12. Makarova L.N. Problemnye zony vzaimodejjstvija prepodavatelejj i studentov [Problem areas of interaction between teachers and students] / L. N. Makarova, M. V. Startsev // Social'no-ehkonomicheskie javlenija i processy [Socio-economic phenomena and processes]. ‑2017. ‑Vol. 12. ‑No. 5. ‑pp. 210-216 [in Russian]
  13. Göncz A. The influence of students’personality traits on their perceptionof a good teacher within the five-factor model of personality /A.Göncz, L.Göncz, J. Pekić // Acta Polytechnica Hungarica. 2014; 11: 65–86. DOI:10.12700/APH.11.03.2014.03.5.
  14. Göncz L. Teacher personality: a review of psychological researched guidelines for a more comprehensive theory in educational psychology /Göncz// Open Review of Educational Research. 2017; 4(1): 75-95. DOI: 10.1080/23265507.2017.1339572.
  15. Romanov D.K. Psychological aspects of perception and understandings of teachers by university students / K. Romanov, L.M. Dauksha // Integration of Education. 2016; 2(20): 228-237. DOI: 10.15507/1991-9468.083.020.201602.228-237.
  16. Vysshaja matematika dlja ehkonomistov [Higher Mathematics for economists] / [N.Sh. Kremer et al .]; edited by Prof. H.S. Kremer. - 3rd ed. - Moscow: UNITY-DANA, 2010. -479 p. [in Russian]