ПРИМЕНЕНИЕ СВЧ БРЭГГОВСКИХ СТРУКТУР ДЛЯ ИЗМЕРЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

ПРИМЕНЕНИЕ СВЧ БРЭГГОВСКИХ СТРУКТУР ДЛЯ ИЗМЕРЕНИЯ КОМПЛЕКСНОЙ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ

Научная статья

Насыбуллин А.Р.^1, *, Фархутдинов Р.В.², Ишкаев Т.М.³, Самигуллин Р.Р.⁴

¹ ORCID: 0000-0001-7802-8212;

² ORCID: 0000-0002-4188-5090;

³ ORCID: 0000-0001-8263-2391;

⁴ ORCID: 0000-0002-2465-9438;

^{1, 2, 3, 4} Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ, Казань, Россия

* Корреспондирующий автор (aydar.nasybullin[at]mail.ru)

Аннотация

В статье рассматриваются общие принципы измерительного преобразования комплексной диэлектрической проницаемости различных материальных сред на сверхвысоких частотах применительно к новому типу преобразовательных элементов, состоящих из электродинамической структуры с резонансом Брэгга. В СВЧ диапазоне подобные структуры реализуются в отрезках волноводов введением системы периодических неоднородностей или нерегулярностей. Решается модельная задача для оценки чувствительности измерений с целью выявления ключевых особенностей и закономерностей в поведении брэгговской структуры, применяемой в качестве сенсора. Полученные результаты могут быть использованы при проектировании СВЧ датчиков для диэлектрического контроля материалов и веществ.

Ключевые слова: Брэгговский резонанс, комплексная диэлектрическая проницаемость, СВЧ волноводы, периодические структуры.

MEASURING COMPLEX PERMITTIVITY VIA BRAGG MICROWAVE STRUCTURES

Research article

Nasybullin A.R.^1, *, Farkhutdinov R.V.², Ishkaev T.M.³, Samigullin R.R.⁴

¹ ORCID: 0000-0001-7802-8212;

² ORCID: 0000-0002-4188-5090;

³ ORCID: 0000-0001-8263-2391;

⁴ ORCID: 0000-0002-2465-9438;

^{1, 2, 3, 4} A. N. Tupolev Kazan National Research Technical University KAI, Kazan, Russia

* Corresponding author (aydar.nasybullin[at]mail.ru)

Abstract

The article discusses the general principles of measuring the conversion of the complex permittivity of various material media at ultrahigh frequencies in relation to a new type of conversion elements consisting of an electrodynamic structure with a Bragg resonance. In the microwave range, such structures are implemented in waveguide segments by introducing a system of periodic inhomogeneities or irregularities. The research presents a solution to a model problem with the goal of evaluating the sensitivity of measurements in order to identify key features and patterns in the behavior of the Bragg structure used as a sensor. The obtained results can be used in the design of microwave sensors for dielectric control of materials and substances.

Keywords: The Bragg resonance, complex permittivity, microwave waveguides, periodic structures.

Введение

Эффект брэгговского отражения явился фундаментальной основой для построения многих элементов оптической техники, таких, например, как многослойные диэлектрические зеркала и волоконно-оптические решетки Брэгга (ВРБ). В подобных элементах оптическое излучение на определенных длинах волн отражается с близким к единице коэффициентом отражения, что дает возможность построить эффективные селективные и отражательные устройства.

Брэгговские структуры являются частным случаем фотонного кристалла (ФК), а именно его одномерным вариантом. Впервые термин «фотонный кристалл» был введен в 1987 г. американским исследователем Илаем Яблоновичем и предназначался для определения оптического материала с одно-, двух- или трехмерной пространственной периодичностью искусственных включений [1], [2 C.1-7]. В ФК вследствие брэгговского отражения, происходит образование фотонных запрещенных зон для некоторых или всех направлений падения оптического луча в зависимости от типа ФК. В своих исследованиях Яблонович предложил для изучения свойств оптических ФК создавать их аналоги в микроволновом или миллиметровом диапазоне электромагнитных колебаний. Внедрение данного подхода привело к упрощению моделирования работы оптических ФК, а также способствовало повышению интереса к микроволновым ФК. В последние 25 лет количество публикаций, посвященных микроволновым ФК, неуклонно возрастало. Многие идеи и принципы, разработанные для оптических ФК, были успешно перенесены в область СВЧ, что позволило получить принципиально новые функциональные элементы для применения в антенной технике [3 С.405-430], высокоскоростных цифровых системах [4 С.61-76], для построения отражателей, высокодобротных резонаторов, фильтров и линий задержки [5 С.86-101].

Микроволновые ФК, как и их оптические прототипы, обладают широкими перспективами применения в измерительной технике. На текущий момент наиболее развиты сенсорные приложения оптических ФК, которые не ограничиваются датчиками на основе ВРБ. В области СВЧ колебаний брэгговские структуры или ФК применительно к сенсорной тематике представлены недостаточно широко. Известны подходы к реализации датчика деформаций для структурного мониторинга строительных сооружений [6], измерения уровня жидких продуктов [7], многопараметрового измерения полупроводниковых структур [8], измерения диэлектрических пластин [9].

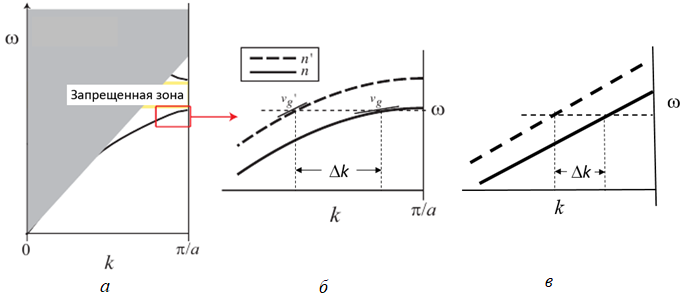
Особое значение указанные структуры могут получить при измерении диэлектрической проницаемости веществ в СВЧ диапазоне. Преимуществом использования брэгговских структур перед традиционными элементами диэлектрического анализа является увеличение чувствительности измерения. Доказательством данного факта может послужить работа [10], посвященная исследованию одномерной периодической структуры в оптическом интегральном исполнении для реализации перестраиваемой линии задержки. В работе показано, что благодаря стремлению к нулю групповой задержки υ_g (производная от дисперсионной кривой ω-k) при приближении к границам запрещенной зоны (полосы заграждения), изменение волнового числа Δk на заданной частоте ω при малом приращении показателя преломления n будет больше, чем для случая отсутствия периодической структуры. Сказанное поясняет (см. рисунок 1).

Рис. 1 – Дисперсионная кривая периодической структуры при малом приращении показателя преломления: а) общий вид дисперсионной характеристики периодической структуры; б) возмущение показателя преломления в периодической структуре; в) возмущение показателя преломления без периодической структуры

 

Изменение показателя преломления оптической интегральной структуры аналогично изменению диэлектрической проницаемости внешней среды для аналогичной периодической структуры в СВЧ диапазоне. Следовательно, фазовый сдвиг ΔkL, где L – длина структуры, окажется наибольшим на границах полосы заграждения и чувствительность к изменению диэлектрической проницаемости будет максимальна. В данной статье производится анализ измерительной задачи определения действительной и мнимой частей относительной комплексной диэлектрической проницаемости (ОКДП):

      (1)

Математическая модель СВЧ брэгговской структуры

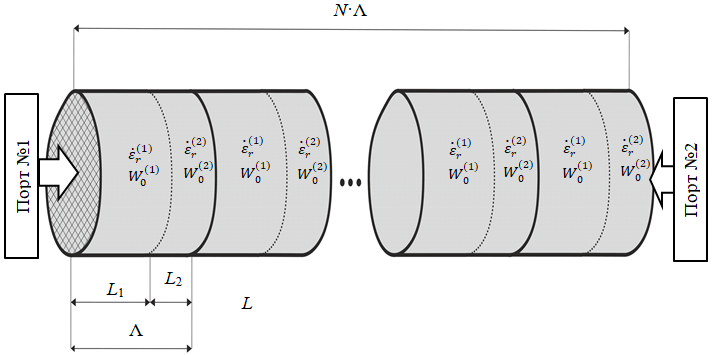
Оценку измерительных возможностей брэгговских СВЧ структур (БСВЧС) проведем на основе математического моделирования эквидистантной брэгговской структуры, представленной в виде кусочно-регулярного волновода с кусочно-однородным заполнением. Под однородностью будем понимать постоянство значений ОКДП диэлектрического материала участка линии, а под регулярностью – неизменность размеров и формы поперечных сечений проводящих элементов вдоль продольной оси линии. В кусочно-однородных и кусочно-регулярных линиях переходы между областями с однородным заполнением и с регулярным сечением имеют скачкообразный характер. Ограничимся случаями, когда переходы между различными диэлектриками и участками волновода с разными сечениями совпадают. Формально модель такой структуры может быть представлена в виде, показанном на рисунке 2. Условие эквидистантности выражается в наличии одинаковых повторяющихся элементарных ячеек длиной Λ, каждая из которых состоит из каскадного соединения двух участков волновода с длинами L₁ и L₂, заполненные диэлектриками с ОКДП  и обладающими множителями волнового сопротивления , смысл которых будет пояснен ниже. Общее количество ячеек обозначим как N.

Рис. 2 – Условное изображение эквидистантной брэгговской структуры

 

Интересующими нас электромагнитными характеристиками выступают частотная зависимость модуля и фазы коэффициента отражения (КО) и коэффициента передачи (КП) волновода. Частотные зависимости КО и КП являются основными информационно-измерительными характеристиками, несущими отклик на изменение обеих частей ОКДП. Поставленная модельная задача может быть решена различными способами, например, методами волновых или классических матриц передачи, трансформации импеданса, согласования волн, конечных разностей, конечных элементов и др.

Если предположить, что в регулярном волноводе может распространяться только основной тип волны, то можно воспользоваться распространенным в теории длинных линий методом трансформации импеданса для расчета полного сопротивления в произвольной точке неоднородной линии. Известно, что любой волновод может быть представлен в виде эквивалентной длинной линии. В этой линии распространяются эквивалентные волновые напряжения и токи, которые физически существуют только в случае ТЕМ-волн, а для всех остальных типов распространяющихся электромагнитных колебаний являются фиктивными. Введение понятий падающих и отраженных волн тока и напряжения позволяет говорить о волновом сопротивлении эквивалентной линии Z₀. Значение величины Z₀ уникально только для линий передачи с TEM-волнами, а для всех остальных типов волн может быть задана различными способами. Волновое сопротивление в общем случае определяется как

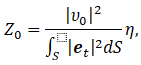      (2)

где η – характеристическое сопротивление среды, равное  – вектор поперечного электрического поля, S – поперечное сечение волновода,  v₀ – нормирующая константа, имеющая размерность напряжения.

Выражение (2) можно записать в следующем виде

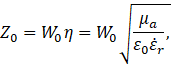       (3)

где  назовем множителем волнового сопротивления. Из (3) видно, что  зависит только от формы поперечного сечения и распределения поля. Значение величины  влияет исключительно на абсолютное значение волнового сопротивления, в то время как η определяет также и фазу.

Помимо волнового сопротивления, которое остается постоянным в пределах регулярного и однородного отрезка эквивалентной линии, в каждой точке вдоль оси z в линии существует входное сопротивление, определяемое как отношение полного эквивалентного напряжения к полному эквивалентному току. Термин «полное» означает сумму падающей и отраженной волн.

Метод трансформации импеданса основан на представлении чередующихся областей волновода в виде отрезков эквивалентных линий передач с волновым сопротивлением . Далее производится расчет входного сопротивления каждой линии поочередно начиная с нагрузки. Условимся, что диэлектрики могут обладать произвольными потерями, следовательно, отрезки с диэлектриками характеризуются комплексными волновыми сопротивлениями.

В основе метода лежит известное выражение для входного сопротивления в любой точке длинной линии, расположенной на расстоянии l от нагрузки 

     (4)

где  – комплексный коэффициент распространения в лини, α – коэффициент затухания, β – волновое число. Параметры   зависят от .

Используя (4) для структуры, изображенной на рисунке 2, можно определить входное сопротивление в каждом сечении линии, соответствующем переходу между диэлектриками и разными сечениями линии:

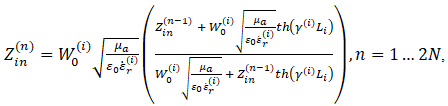     (5)

где n – порядковый номер сечения. Нумерация производится от сечения с n=0, к которому подключена нагрузка. Для случая, когда нагрузка подключена к порту 2, а источник – к порту 1 (см. рисунок 2) в (5) будет i=1, если n – четное и i=2, если n – нечетное. Для случая, когда нагрузка подключена к порту 1, а источник – к порту 2 в (5) будет i=1, если n – нечетное и i=2, если n – четное. Согласно основной идее метода трансформации импеданса, первоначально находится входное сопротивление в сечении с n=0, которое равно сопротивлению нагрузки . Далее рекуррентно по формуле (5) рассчитываются входные сопротивления . В каждом сечении существует коэффициент отражения, выражаемый как

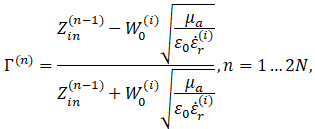     (6)

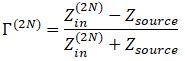Коэффициент отражения от сечения, к которому подключен источник, согласно (6) можно найти следующим образом      (7)

где  – внутреннее сопротивление источника.

Полное эквивалентное напряжение  в каждом сечении n можно определить через коэффициент передачи ячейки по напряжению  как

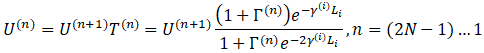     (8)

Для того чтобы найти значение полного напряжения на нагрузке, необходимо задать амплитуду падающей волны напряжения на входе волновода  и определить полное напряжение на входе как

     (9)

Далее, используя выражение (8), последовательно вычисляются значения  при n=(2N-1)…0. Обладая значениями напряжения на входе и выходе волновода , возможно рассчитать коэффициент передачи волновода по напряжению

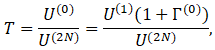     (10)

где 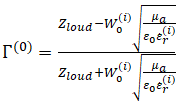 – коэффициент отражения от нагрузки.

Выражения (7) и (10) позволяют отыскать элементы матрицы рассеяния всего волновода, а именно коэффициенты отражения S₁₁ и прохождения S₂₁ в виде

     (11)

     (12)

где в качестве  используются волновые сопротивления подводящих линий. Коэффициенты S₁₂ и S₂₂ находятся аналогично по формулам (5)-(12) при замене источника на нагрузку и наоборот.

Результаты моделирования

Общая формула для брэгговской частоты при произвольных ,  и  будет выглядеть как

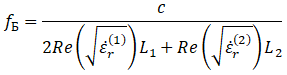     (13)

где  – пространственный период структуры, c – скорость света.

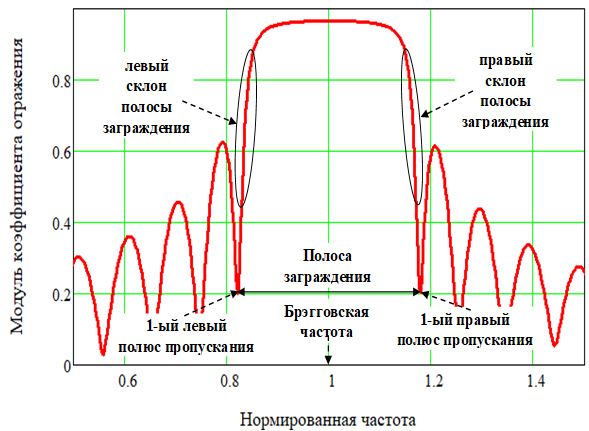
Частотную характеристику коэффициента отражения периодической СВЧ-структуры удобно представить как функцию от нормированной частоты  определяется через (13). Пример такой характеристики можно наблюдать на рисунке 3, там же указаны названия основных характерных элементов, которые будут в дальнейшем в работе использоваться. Периодичность в расположении частотных полос заграждения приводит к появлению понятий вторая, третья и т.д. полосы заграждения. Центральные частоты этих полос заграждения будут кратны основной брэгговской частоте согласно номеру полосы.

Рис. 3 – Типичная частотная характеристика коэффициента отражения периодической СВЧ-структуры в области брэгговского резонанса

 

На рисунке 3 также указаны названия основных участков характеристики брэгговской структуры.

Проведем численное моделирование задачи измерения реальной и мнимой частей ОКДП с помощью чувствительного элемента в виде эквидистантной БСВЧС. Примем за измеряемую величину , а значение  будем считать заданным. Эффективность чувствительного элемента в первую очередь определяется его чувствительностью, показывающей, насколько сильно изменится выходной сигнал преобразователя при малой вариации измеряемой величины. Будем анализировать изменения частотных характеристик БСВЧС при малой вариации величин . Для оценки степени этого изменения введем параметр чувствительности:

     (14)

где F – функция, определяющая значение выходной величины, то есть модуль или фаза КО или КП, определяемые по формулам (11) и (12), x – входная величина, то есть . Таким образом следует определить следующие зависимости , в обозначении которых для удобства индекс (2) у измеряемых проницаемостей опускается.

В качестве исходных данных для вычислительного эксперимента выберем следующие параметры:  количество ячеек N=10. Выберем равные между собой множители волновых сопротивлений и электрические длины двух участков, составляющих ячейку периодической структуры, то есть

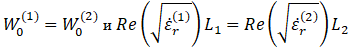      (15)

Последнее выражение в условии (15) приводит к тому, что в частотной характеристике КО БСВЧС можно наблюдать только полосы заграждения с нечетными номерами. Также при соблюдении указанного условия форма частотных характеристик для полос заграждения не зависит от абсолютных значений величин L₁ и L₂, а при их вариации наблюдается только смещение характеристик по частоте.

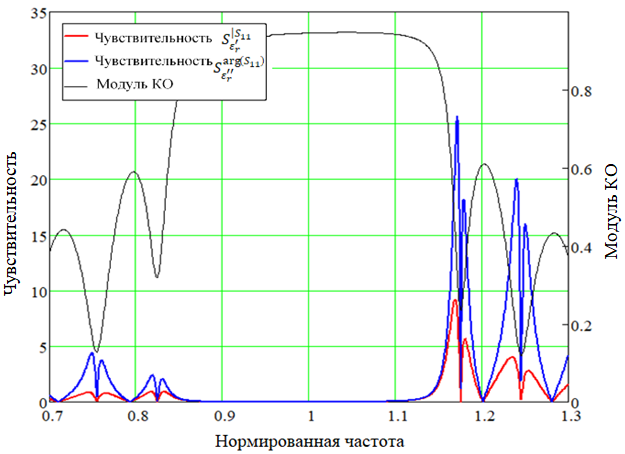
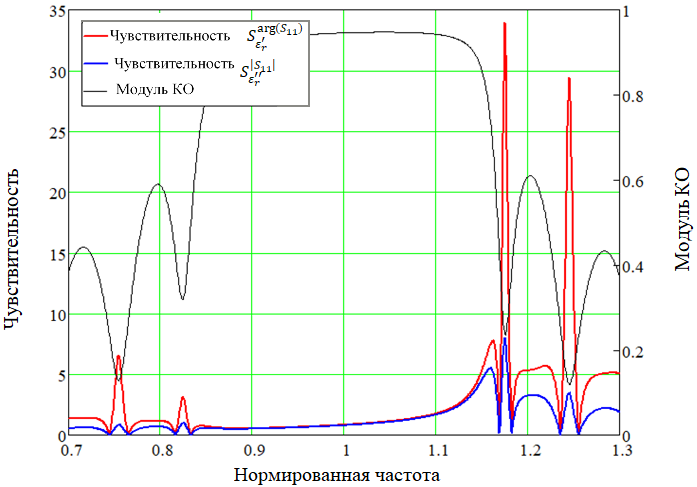
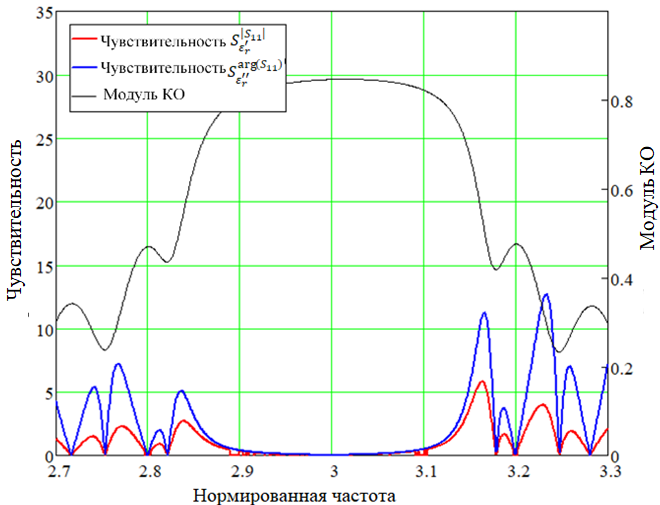
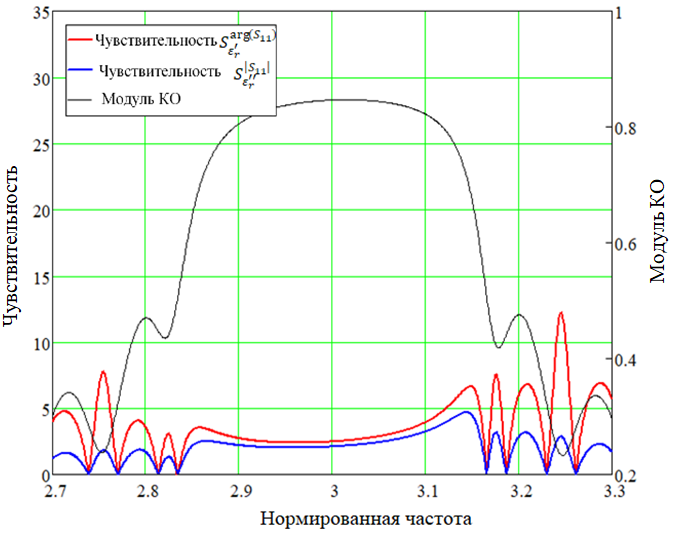
По формуле (14) методом численного дифференцирования были определены частотные зависимости параметров чувствительности. Проведем анализ полученных зависимостей применительно к КО с целью определения частотных областей с максимальной чувствительностью. На рисунках 4 и 5 показаны характеристики   для первой полосы заграждения, а на рисунке, а на рисунках 6 и 7 – для третьей. Как можно наблюдать из графиков, присутствует существенная неравномерность в частотной зависимости параметров чувствительности

Подробно анализируя зависимости на рисунках 4-7, можно сделать следующие выводы:

• Максимальная чувствительность наблюдается на правом склоне полосы заграждения.
• Зависимости 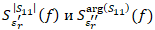 обладают максимумами и минимумами в одинаковых частотных точках, при этом глобальный максимум приходится на нижнюю область правого склона полосы заграждения.
• Зависимости 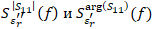 обладают максимумами и минимумами в одинаковых частотных точках, при этом глобальный максимум приходится на первый правый полюс пропускания.
• Зависимости 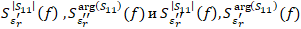 имеют противоположные максимумы и минимумы.
• Третьей полосе заграждения характерно уменьшение максимальных абсолютных значений чувствительностей по сравнению с первой полосой, но наблюдается расширение областей частот с максимальной чувствительностью.

 

Рис. 4 – Характеристики чувствительности для КО для первой полосы заграждения

Рис. 5 – Характеристики чувствительности для КО для первой полосы заграждения

Рис. 6 – Характеристики чувствительности для КО для третьей полосы заграждения

Рис. 7 – Характеристики чувствительности для КО для третьей полосы заграждения

Представленные выше сведения справедливы также для КП, отличие будет заключаться только в абсолютных значениях максимально достижимых чувствительностей. Примечательным фактом является изменение положения частотных точек с максимальной чувствительностью, а именно переход в область расположения левого склона полосы заграждения, при значениях измеряемой величины .

Заключение

Проведенные исследования позволяют сформулировать рекомендации к методике измерения комплексной диэлектрической проницаемости материальных сред с применением СВЧ брэгговских структур. Наличие участков частотных характеристик брэгговской структуры с повышенной чувствительностью позволяет проводить расчет искомой комплексной диэлектрической проницаемости по результатам измерения модуля и фазы КО или КП только в ряде частотных точек. Данное обстоятельство позволит сократить время расчета и обеспечит повышение точности результата измерения.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics / E. Yablonovitch // Physical Review Letters, – Vol. 58, N. 20. – P. 2059-2062.
2. Inoue K. Photonic Crystals: Physics, Fabrication and Applications / K. Inoue, K. Ohtaka // – Berlin [and etc.]: Springer-Verlag, 2004. – 320 p.
3. Minin I. Microwave and Millimeter Wave Technologies: from Photonic Bandgap Devices to Antenna and Applications / I. Minin (ed.) // – Vukovar: In-Tech, 2010. – 468 p.
4. Orlandi A. Electromagnetic Bandgap (EBG) Structures: Common Mode Filters for High-Speed Digital Systems / A. Orlandi, B. Archambeault, F.D. Paulis, S. Connor // Hoboken: John Wiley & Sons, 2017. – 221 p.
5. Martín F. Artificial Transmission Lines for RF And Microwave Applications / F. Martín // Hoboken: John Wiley & Sons, 2015. – 520 p.
6. Huanga J. Coaxial cable Bragg grating sensors for large strain measurement with high accuracy / J. Huanga, T. Weia, X. Lana, J. Fanb, H. Xiao // Proc. of SPIE. – 2012. – Vol. 8345. – P. 83450Z.
7. Насыбуллин А.Р. Преобразовательный элемент измерителя уровня жидких продуктов на основе брэгговской СВЧ-структуры в коаксиальном кабеле / А.Р. Насыбуллин, О.Г. Морозов, А.А. Севастьянов, Р.В. Фархутдинов, Р.Р. Самигуллин // Современные проблемы науки и образования. – 2014. – № 6. – [Электронный ресурс] : URL: https://www.science-education.ru/ru/article/view?id=16390 (дата обращения: 24.11.2020)
8. Усанов Д.А. Многопараметровые измерения эпитаксиальных полупроводниковых структур с использованием одномерных сверхвысокочастотных фотонных кристаллов / Д.А. Усанов, С.А. Никитов, А.В. Скрипаль, Д.В. Пономарев, Е.В. Латышева // Радиотехника и электроника. – 2016. – Т.61, №1. – С. 45-53.
9. Усанов Д.А. Измерение параметров диэлектриков с использованием СВЧ коаксиальной брэгговской структуры / Усанов Д.А., Никитов С.А., Скрипаль А.В., Пономарев Д.В., Рузанов О.М., Тимофеев И.О. // Радиотехника. – 2019. – Т.83, №7. – С. 6-12.
10. Povinelli M.L. Slow-light, band-edge waveguides for tunable time delays / M.L. Povinelli, S.G. Johnson, J.D. Joannopoulos // Optics Express. – 2005. – Vol. 13, No. 18. – P. 7145-7159.

Список литературы на английском языке / References in English

1. Yablonovitch E. Inhibited spontaneous emission in solid-state physics and electronics / E. Yablonovitch // Physical Review Letters, – Vol. 58, N. 20. – P. 2059-2062.
2. Inoue K. Photonic Crystals: Physics, Fabrication and Applications / K. Inoue, K. Ohtaka // – Berlin [and etc.]: Springer-Verlag, 2004. – 320 p.
3. Minin I. Microwave and Millimeter Wave Technologies: from Photonic Bandgap Devices to Antenna and Applications / I. Minin (ed.) // – Vukovar: In-Tech, 2010. – 468 p.
4. Orlandi A. Electromagnetic Bandgap (EBG) Structures: Common Mode Filters for High-Speed Digital Systems / A. Orlandi, B. Archambeault, F.D. Paulis, S. Connor // Hoboken: John Wiley & Sons, 2017. – 221 p.
5. Martín F. Artificial Transmission Lines for RF And Microwave Applications / F. Martín // Hoboken: John Wiley & Sons, 2015. – 520 p.
6. Huanga J. Coaxial cable Bragg grating sensors for large strain measurement with high accuracy / J. Huanga, T. Weia, X. Lana, J. Fanb, H. Xiao // Proc. of SPIE. – 2012. – Vol. 8345. – P. 83450Z.
7. Nasybullin A. R. Preobrazovatel'nyj jelement izmeritelja urovnja zhidkih produktov na osnove brjeggovskoj SVCh-struktury v koaksial'nom kabele [Transformative Element of The Liquid Product Level Meter Based On The Bragg Microwave Structure In A Coaxial Cable] [Electronic resource] / A. R. Nasybullin, O. G. Morozov, A. A. Sevastyanov et al. // Sovremennye problemy nauki i obrazovanija. [Modern Problems of Science and Education.] - 2014. - No. 6. - [Electronic resource] : URL: https://www.science-education.ru/ru/article/view?id=16390 (accessed: 24.11.2020) [in Russian]
8. Usanov D. A. Mnogoparametrovye izmerenija jepitaksial'nyh poluprovodnikovyh struktur s ispol'zovaniem odnomernyh sverhvysokochastotnyh fotonnyh kristallov [Multiparameter Measurements of Epitaxial Semiconductor Structures Using One-Dimensional Ultrahigh-Frequency Photonic Crystals] / D. A. Usanov, S. A. Nikitov, A.V. Skripal et al. // Radiotehnika i jelektronika. [Radio Engineering and Electronics.] - 2016. - Vol. 61, No. 1. - pp. 45-53 [in Russian]
9. Usanov D. A. Izmerenie parametrov dijelektrikov s ispol'zovaniem SVCh koaksial'noj brjeggovskoj struktury [Measurement of Parameters of Dielectrics Using Microwave Coaxial Bragg Structure] / D. A. Usanov, S. A. Nikitov, A.V. Skripal // Radiotehnika. [Radio Engineering.] - 2019. - Vol. 83, No. 7. - pp. 6-12 [in Russian]
10. Povinelli M.L. Slow-light, band-edge waveguides for tunable time delays / M.L. Povinelli, S.G. Johnson, J.D. Joannopoulos // Optics Express. – 2005. – Vol. 13, No. 18. – P. 7145-7159.