МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ НАНОЧАСТИЦ В ЖИДКОСТИ В ПРОЦЕССЕ ИХ ОСАЖДЕНИЯ

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ НАНОЧАСТИЦ В ЖИДКОСТИ В ПРОЦЕССЕ ИХ ОСАЖДЕНИЯ

Научная статья

Хуссейн С.М.Р.Х.^1, *, Морозов О.Г.², Данилаев М.П.³, Куклин В.А.⁴, Анфиногентов В.И.⁵, Сахабутдинов А.Ж.⁶, Сахабутдинова Г.И.⁷

¹ ORCID:0000-0001-6022-0548;

² ORCID:0000-0003-4779-4656;

³ ORCID: 0000-0002-7733-9200;

⁵ ORCID:0000-0003-0015-2429;

⁶ ORCID:0000-0002-0713-7806;

⁷ ORCID: 0000-0002-5570-3083;

¹ Университет Кербелы, Кербела, Ирак;

^2-7 Казанский национальный исследовательский технический университет им. А.Н. Туполева‑КАИ, Казань, Россия

* Корреспондирующий автор (safaa_m333[at]yahoo.com)

Аннотация

В работе предлагается математическая модель динамического измерения концентрации полимерной оболочки на поверхности дисперсных частиц их наполнителя, взвешенных в жидкости в процессе их седиментации. Математическая модель предусматривает движение осаждаемых частиц под действием силы тяжести, гидростатической подъемной силы, силы сопротивления движении. В модели учитывается влияние броуновского (теплового) движения растворителя на перемещение частиц на основе упругого столкновения, влияние неупругого столкновения частиц друг с другом. Кроме того, учитывается влияние движения жидкости под действием градиента температуры на движение осаждаемых частиц, для чего построена математическая модель движения жидкости. Оценка концентрации частиц осуществляется на основе моделирования рассеяния Рэлея. Проведено сравнение данных расчетов с результатами натурного эксперимента.

Ключевые слова: седиментация, математическая модель, осаждение частиц в жидкости, измерение молекулярной массы, измерение наночастиц, измерение концентрации, рассеяние Рэлея, численное интегрирование.

A MATHEMATICAL MODEL FOR MEASURING THE CONCENTRATION OF NANOPARTICLES IN LIQUID DURING THEIR DEPOSITION

Research article

Hussein S.M.R.Kh.^1, *, Morozov O.G.², Danilaev M.P.³, Kuklin V.A.⁴, Anfinogentov V.I.⁵, Sakhabutdinov A.Zh.⁶, Sakhabutdinova G.I.⁷

¹ ORCID:0000-0001-6022-0548;

² ORCID:0000-0003-4779-4656;

³ ORCID: 0000-0002-7733-9200;

⁵ ORCID:0000-0003-0015-2429;

⁶ ORCID:0000-0002-0713-7806;

⁷ ORCID: 0000-0002-5570-3083;

¹ University of Karbala, Karbala, Iraq;

^2-7 A. N. Tupolev‑Kazan National Research Technical University KAI, Kazan, Russia

* Corresponding author (safaa_m333[at]yahoo.com)

Abstract

The article offers a mathematical model for dynamic measurement of the polymer enclosure concentration on the surface of dispersed particles of their filler suspended in a liquid during their sedimentation. The mathematical model provides for the movement of deposited particles under the influence of gravity, hydrostatic lift, and drag forces. The model takes into account the effect of Brownian (thermal) motion of the solvent on the movement of particles based on elastic collision as well as the effect of the inelastic collision of particles with each other. In addition, the model considers the influence of fluid motion under the influence of a thermal gradient on the motion of deposited particles, for which a mathematical model of fluid motion is constructed. The particle concentration is estimated based on Rayleigh scattering modeling. The calculation data are compared with the results of a full-scale experiment.

Keywords: sedimentation, mathematical model, particle deposition in a liquid, molecular mass measurement, nanoparticle measurement, concentration measurement, Rayleigh scattering, numerical integration.

Введение

Один из подходов к управлению механическими свойствами дисперсно-армированных полимерных композитов основан на формировании полимерной оболочки на поверхности дисперсных частиц их наполнителя [1], [2]. При формализации математических моделей механических свойств таких композитов учитываются механические свойства полимерной матрицы, дисперсных частиц, а также полимерной оболочки на поверхности этих частиц [3]. В то же время вопрос об определении количественных и численных значений механических свойств полимерных оболочек остается открытым. Это связано с тем, что толщина полимерной оболочки может варьироваться от единиц до десятков нанометров. Напрямую измерить механические свойства (модуль Юнга, коэффициент Пуассона и ряд других) полимерных оболочек невозможно. Однако существует подход, позволяющий определить механические характеристики полимерных частиц, оценив молекулярную массу полимера и уточнив необходимые механические характеристики с использованием табличных данных [4].

Один из подходов к измерению молекулярной массы полимера основан на анализе процесса и продолжительности осаждения молекул полимера и частиц наполнителя в растворителе. Молекулы полимера легче частиц наполнителя. Поэтому сначала осаждаются частицы наполнителя, затем осаждаются частицы полимера. Определение постоянной времени седиментации основано на анализе зависимости концентрации частиц от времени. Эта постоянная времени седиментации является начальным параметром для оценки средней молекулярной массы полимера.

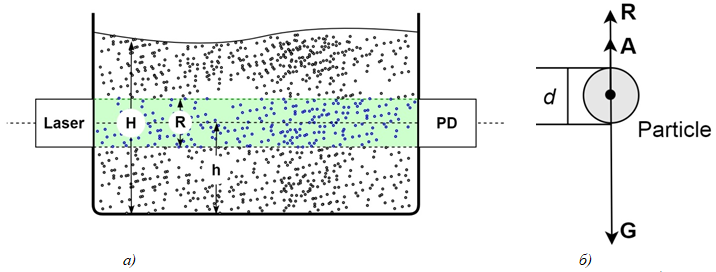
В работе предлагается математическая модель динамического измерения концентрации двух типов взвешенных в жидкости частиц в процессе их осаждения, основанная на управлении рассеянием света при прохождении лазерного излучения через раствор с взвешенными частицами. Измерительная система представляет собой кварцевую кювету, в которой находится раствор частиц, покрытых полимерной оболочкой в растворителе (рисунок рис. 1а).

 

Рис. 1 – Измерительная система: схема (а); Силы, действующие на частицу в жидкости (б): G – сила тяжести, A – сила Архимеда, R – сила сопротивления движению, d – диаметр частицы

 

Под действием растворителя полимер оболочки частично растворяется. Под действием силы тяжести происходит осаждение частиц двух типов (молекулы полимера, наполнитель). Луч лазера направляется в раствор с одной стороны кварцевой кюветы. Фотоприемник находится на другой стороне кюветы. Лазерное излучение, проходя через раствор, претерпевает рассеяние Рэлея, которое влияет на интенсивность света на фотоприемнике. Концентрация частиц в области лазерного луча прямо пропорциональна интенсивности света на фотоприемнике. Моделируется временная динамика общей площади частиц, покрывающих лазерный луч.

Измерительная система состоит из кварцевой кюветы (рисунок рис. 1а), в который наливают растворитель этилацетат. Частицы оксида алюминия (Al₂O₃), покрытые полимерными волокнами, помещают в растворитель и встряхивают.

Под воздействием растворителя частицы оксида алюминия и полимера разделяются. Под действием силы тяжести частицы начинают оседать на дно кварцевой кюветы. Лазерное излучение направляется в кварцевую кювету, на другом конце которой устанавливается фотоприемник. Со временем частицы осядут, и общий свет, проходящий через кювету, также изменится. Задача состоит в моделировании изменения оптической мощности лазерного луча, проходящего через кварцевую кювету, при осаждении частиц.

Уравнение движения частицы

Движение одиночной частицы под действием сил гравитации, гидростатической подъемной силы и силы сопротивления движению описывается уравнением:

        (1)

где A_i – сила Архимеда, G_i – сила гравитации, R_i – сила сопротивления движению, W_i – скорость, M_i – масса i-ой частицы, и T – время. Нижний индекс i указывает на отдельную частицу. Силы, действующие на частицу, показаны на рисунке рис. 1б.

Сила гравитации G_i равна произведению массы частицы M_i и ускорения свободного падения g. Гидростатическая подъемная сила Архимеда A_i противоположно направлена силе гравитации G_i и равна произведению объема частицы, вычисляемого через диаметр частицы D_i, на плотность жидкости r и ускорения свободного падения. Сила сопротивления движению R_i противоположно направлена скорости движения частицы W_i, и пропорциональна произведению квадрата скорости, плотности жидкости, площади поперечного сечения частицы и числу Рейнольдса Re, связанному с коэффициентом динамической вязкости η жидкости. Уравнение движения частицы (1) после подстановки в него физических параметров задачи примет вид:

      (2)

Уравнение (2) может быть преобразовано в безразмерный вид, если ввести четыре характерных параметра задачи, а именно: характерные размер (L₀), массу (M₀), время (T₀), и температуру (K₀). Определив безразмерные переменные: w – скорость, m – массу, d – диаметр и τ – время, получим уравнение движения в безразмерных переменных примет вид:

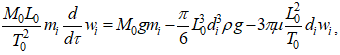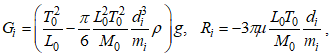       (3) которое можно преобразовать, разделив на коэффициент, стоящий в левой части:        (4) введя два безразмерных комплекса:         (5)

что дает окончательную форму уравнения движения частицы в жидкости в безразмерной форме, удобной для интегрирования.

Влияние броуновского (теплового) движения жидкости

Кроме сил, действующих на частицу, в силу своего малого веса она подвержена броуновскому (тепловому) движению молекул жидкости. Скорость броуновского движения жидкости зависит от температуры жидкости, которая вблизи частицы может быть аппроксимирована как линейная комбинация температур на верхней K_T и нижней K_B границе жидкости.

Используя модель упругого столкновения частицы с массой m_i и скоростью w_i с молекулой жидкости с массой m и скоростью w, и определив среднюю кинетическую энергию молекул как функцию температуры [2], запишем выражение для вертикальной w_i составляющей скорости:

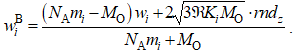       (6)

где N_A – число Авогадро, u_i и w_i – составляющие скоростей частицы до столкновения. Выражение для горизонтальной составляющей скорости u_i описывается аналогично. В (6) введено разделение броуновской составляющей скорости молекул на две (w_i^B – вдоль вертикальной оси oz и u_i^B – в горизонтальной плоскости oxy) путем введения двух переменных rnd_x и rnd_z, где rnd_x и rnd_z две случайные величины, сумма квадратов которых равна единице, и которые описывают случайный характер направления броуновского столкновения.

Изменение положений частиц под действием влияния броуновского движения, описывается связью скорости и перемещения и корректируют новые положения частиц, вызванные изменением скоростей частиц под действием броуновского движения.

Столкновение частиц друг с другом

Если две частицы с координатами z_i и z_j (и скоростями w_i и w_j) находятся рядом друг с другом, существует ненулевая вероятность их неупругого столкновения. Вероятность столкновения частиц может быть вычислена как отношения суммы площадей, которые могут покрыть частицы при их перемещении в горизонтальной плоскости, к площади горизонтальной поверхности кюветы. Если вероятность столкновения частиц больше, чем произвольное случайное число, предполагается что частицы не упруго сталкиваются и слипаются. При этом считаем, что i‑ая частица принимает новую массу, скорость и диаметр, а j‑ая частица пропадает. Новая масса, скорость, диаметр и новая координата i‑ой частицы определяются по соотношениям:

      (7)

Новая скорость, новый диаметр и новая координата j-ой частицы будут равны нулю. Число частиц соответствующего типа, соответствующего j-ой частице уменьшается на единицу.

Конечно-разностная схема

Уравнение (4) будем решать численно для каждой частицы в отдельности, записав его в конечно-разностной форме:

      (8)

где q – параметр конечно-разностной схемы [5], Δτ – шаг интегрирования, n – индекс интегрирования, определяющий дискретное время. Выражение (8) позволяет записать выражение для скорости и координаты частицы в дискретный момент времени n×Δτ в конечно-разностной форме:

   (9)

Рассеяние Рэлея, вызванное частицами в области лазерного луча

Обозначим высоту кварцевой кюветы за H. Лазерный луч, проходящий через жидкость в кювете, описывается круглым цилиндром с радиусом основания R, расположенным на высоте h. Поперечное сечение лазерного луча показано на рисунке рис. 2Рис. 2.

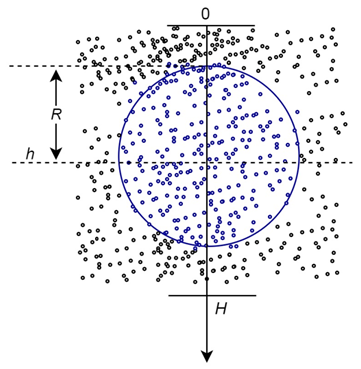
Рис. 2 – Поперечное сечение лазерного луча: H – высота кюветы; h – положение лазерного луча и R – его радиус

  Полный свет, загораживаемый частицами в области лазерного луча, может быть смоделирован выражением: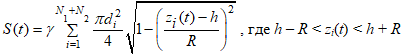       (10) где d_i – диаметр частицы, z_i – ее координата, γ – коэффициент пропорциональности, t – время.

Начальные условия для интегрирования движения частиц

Рассмотрим два типа частиц в жидкости. Каждый тип имеет нормальное распределение масс, диаметров и плотностей. Все частицы распределены в жидкости в начальный момент времени равномерно по всему объему жидкости и с нулевыми скоростями. Обозначим количество частиц первого и второго типов как N₁ и N₂. Следовательно, общее количество частиц будет суммой N = N₁ + N₂. Введем в рассмотрение функцию распределения:

       (11)

где f_avg – среднее значение, f_disp – дисперсия, и rnd(1) – произвольная случайная величина в диапазоне [0, 1]. Используя последовательную нумерацию частиц, пронумеруем все частицы так, чтобы первые N₁ частиц были частицами первого типа, а следующие N₂ частиц были частицами второго типа. Распределение диаметров и плотностей частиц запишем через функцию распределения, как:

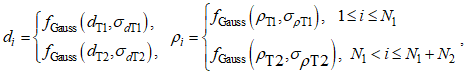      (12)

где d_T1 и d_T2 средние диаметры, σ_dT1 и σ_dT2 – дисперсии диаметров, ρ_dT1 и ρ_dT2 – средние плотности, σ_rT1 и σ_rT2 – дисперсии плотностей частиц первого и второго типов, соответственно. Далее, зная диаметры и плотности частиц определим их массы: m_i = π/6×ρ_i×d_i³, что позволяет вычислить безразмерные комплексы для каждой частицы согласно (5).

Движение жидкости под действием градиента температур

Предложенная выше математическая модель не предполагает учет движения жидкости. Вместе с тем, разность температур на границе кюветы приводит к движению жидкости. Учитывая крайне малый вес осаждаемых частиц, невозможно исключить влияние движения жидкости на перемещение частиц. Смоделируем движение жидкости в кювете под действием перепада температур, предположив, что частицы не оказывают никакого влияния на движение самой жидкости в виду их малого размера и веса.

Рассмотрим математическую модель движения вязкой несжимаемой жидкости под действием поля температур в плоскости перпендикулярной оси луча лазера. Движение жидкости описывается одним векторным уравнением Навье-Стокса и тремя скалярными – теплопроводности, неразрывности и зависимости плотности от температуры [6], записанная в естественных переменных – скорость, температура, давление, время. Вместе с тем, система уравнений движения жидкости, записанная в естественных переменных, не удобна для ее численного решения.

Уравнения движения жидкости

Запишем ее в переменных функция тока, вихрь и температура [7], введя такие же характерные размерные параметры задачи, как и для движения частиц. Примем во внимание, что движение жидкости в замкнутой кювете под действием перепада температур на верхней и нижней границах при постоянных значениях температуры и без притока или оттока жидкости извне в переменных температура, функция тока и вихрь не будет меняться со временем. С течением времени поле температур можно будет считать установившимся, равно как скорости в каждой точке кюветы. Установившееся поле температуры и скоростей приведет к тому, что и поле функций тока и вихря тоже будет установившимся. Следовательно, систему уравнений следует рассматривать как стационарную систему:

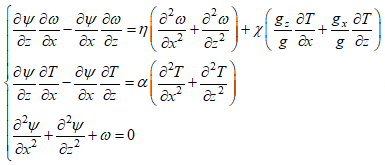      (13) где введены три безразмерных параметра: 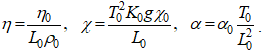      (14)

тут η₀ – динамическая вязкость, α₀ – коэффициент теплопроводности, χ₀ –коэффициент объемного расширения жидкости, g –ускорение свободного падения, K₀ – характерная температура.

Система уравнений (13), записанная в безразмерной форме, не предполагает возможности ее аналитического решения в общем случае. Вместе с тем, она удобна для ее численного решения. Перед решением системы уравнений необходимо дополнить ее граничными условиями.

Начальные и граничные условия

Поскольку уравнения для температуры T, функции тока Ψ и вихря ω стационарны, это не требует задания начальных условий. Формулировка граничных условий для функции тока и вихря на твердых стенках формулируются просто, где достаточно задать условия прилипания, то есть скорость на границе равна нулю. Константа для функции тока на стенках выбирается произвольно. На одной из границ функция тока равна нулю, а на других – функция тока подбирается таким образом, что разница функций между двумя границами равна объемному расходу среды между ними. Поскольку в нашей задаче расход жидкости отсутствует, то функция тока на всех границах задается равной нулю. Таким образом, граничные условия для функции тока определим в виде:

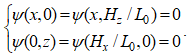     (15)

где H_x и H_z – размеры кюветы вдоль оси Ox и Oz, соответственно, а L₀ – введенный характерный размер задачи.

Граничные условия для поля температур формулируются аналогично (15), с учетом характерной температуры задачи K₀:

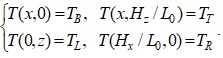       (16)

где T_B и T_T – температура на нижней и верхней, а T_L и T_R – температура на левой и правой границах кюветы.

Граничные условия для вихря определяются из третьего уравнения в (13) как вторая производная от функции тока по нормали к границам кюветы:

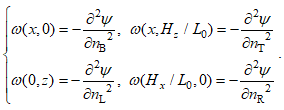    (17)

где n_B, n_T, n_L, n_R – нормаль, построенная к нижней, верхней, левой и правой границам кюветы, соответственно.

Таким образом, система уравнений (13) с граничными условиями (15)–(17) представляют собой полную систему уравнений движения жидкости в поле температур.

Уравнения в конечно-разностной форме

Поскольку система уравнений (13) и каждое уравнение в отдельности в общем случае не предполагает наличия аналитического решения, то систему уравнений (13) будем решать численно. Для чего запишем каждое из уравнений в конечно-разностной форме, и будем искать решение в виде сеточных функций. Для чего разобьем область кюветы на N_x×N_z элементов вдоль осей ox и oz, соответственно. Тогда шаги сетки вдоль осей ox и oz будут равны:

      (18) Значения искомых функций в области будут выражены виде дискретных сеточных функций:      (19)

которые и являются искомыми значениями.

Поскольку алгоритм решения предполагает итерационный процесс, который заключается в последовательном решении каждого уравнения в отдельности, приведем алгоритм решения каждого уравнения отдельно.

Решение уравнения Пуассона для функции тока

Уравнение Пуассона для функции тока представляет собой наиболее простое из уравнений в (13):

      (20)

Уравнение (20), записанное в конечно-разностной форме, с учетом производных, записанных в виде центральных разностей со вторым порядком аппроксимации, будет иметь вид:

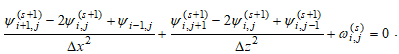      (21)

Записанное для каждой внутренней точки сеточных функций уравнение (21) представляет собой систему уравнений для i = 2, N_x – 1 и j = 2, N_z – 1, что приводит к системе (N_x – 2)´(N_z – 2) штук линейных уравнений. Полученная система уравнений имеет пятидиагональную матрицу с отличием записи уравнений для граничных областей.

Систему уравнений (21) можно решать как методом прогонки, так и методом простой итерации. Метод прогонки в общем случае будет зависеть от вида граничных условий, который скажется на форме записи и виде линейных уравнений на границе области. Можно использовать метод простой итерации, который не зависит от выбора вида граничных условий. Для чего перепишем уравнение (21) разрешив его относительно значения в (i, j) точке и построим еще один итерационный процесс, введя итерационный индекс k для i = 2, N_x – 1 и j = 2, N_z – 1:

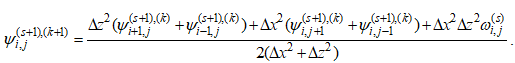      (22) Итерационный процесс, построенный по формуле (22), является сходящимся, условие сходимости можно записать как: 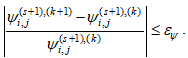      (23) где ε_Ψ заранее заданная погрешность определения поля функций тока. Решение уравнения для поля температуры

Решение второго уравнения в (13) для поля температур T^(s+1) на (s + 1) итерации будем искать в предположении, что значения поля функций тока Ψ^(s+1) на текущей итерации известны. Для чего перепишем его в конечно-разностной форме в каждой точке сеточной функции для i = 2, N_x – 1 и j = 2, N_z – 1. Частные производные в (13) аппроксимируем в виде центральных разностей со вторым порядком аппроксимации:

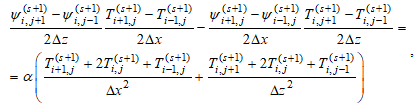     (24)

что приводит к системе (N_x – 2)×(N_z – 2) штук линейных уравнений относительно неизвестных на (s + 1) итерационном шаге значений для поля температур T_i,j. Решение системы уравнений (24) будем искать итерационным методом, для чего разрешим уравнение (24) относительно T_i,j и запишем итерационный процесс, введя итерационную переменную k, в виде:

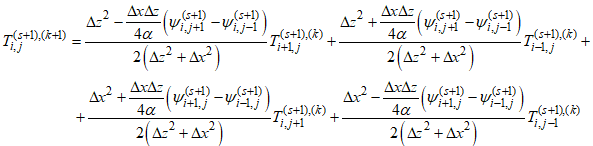      (25) условие сходимости итерационного процесса запишем аналогично (23): 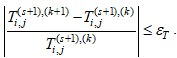      (26) где ε_T заранее заданная погрешность определения поля температуры. Решение уравнения для поля вихря

Решение первого уравнения в (13) для поля вихря ω^(s+1) на (s + 1) итерации будем искать в предположении, что значения поля функций тока ψ^(s+1) и поля температур T^(s+1) на текущей итерации известны. Для чего перепишем его в конечно-разностной форме в каждой точке сеточной функции для i = 2, N_x – 1 и j = 2, N_z – 1. Частные производные в (13) аппроксимируем в виде центральных разностей со вторым порядком аппроксимации:

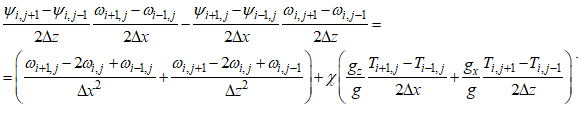      (27)

Уравнение (27), записанное в каждой точке конечно-разностной сетки, приводит к системе (N_x – 2)×(N_z – 2) штук линейных уравнений относительно неизвестных на (s + 1) итерационном шаге значений для поля вихря ω_i,j. Решение системы уравнений (27) будем искать итерационным методом, для чего разрешим уравнение (27) относительно ω_i,j и запишем итерационный процесс, введя итерационную переменную k, в виде:

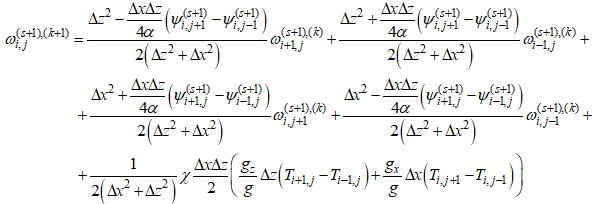      (28) условие сходимости запишем аналогично (23) и (26): 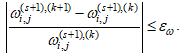      (29) где e_ω заранее заданная погрешность определения поля температуры.

Определение поля скоростей

Конечным результатом моделирования движения жидкости под действием перепада температур является не только определение полей для функции тока, вихря и температур. Основными полями, которые необходимо учитывать при движении осаждаемых частиц являются поля скоростей и температуры. Результат вычислений, выполненный согласно алгоритму, описанному в 0, даст готовое распределение поля температуры.

Распределение поля скоростей (вертикальной и горизонтальной составляющей) можно по формулам связи скоростей с функцией тока, переписав их в конечно-разностной форме с учетом производных, записанных со вторым порядком аппроксимации:

     (30)

что даст готовое стационарное поле скоростей движения жидкости, влияние которого необходимо учесть при моделировании движения частиц.

Алгоритм решения

Алгоритм решения системы уравнений движения жидкости описывается следующей последовательностью действий:

1) задаем граничные условия для функции тока и температуры;

2) задаем начальные приближения для функции тока и вихря равными нулю, а значения поля температур, равными значению на верхней границе. Стартуем итерационный процесс, задав номер итерации s = 0;

3) решаем третье уравнение в (13) – уравнение Пуассона для функции тока ψ^(s+1) на (s + 1) итерации, предполагая поле вихря ω^(s) известным;

4) решаем второе уравнение в (13) для поля температур T^(s+1) на (s + 1) итерации, предполагая поле функций тока ψ^(s+1) на текущей итерации известным;

5) решаем первое уравнение в (13) для поля вихря ω^(s+1) на (s + 1) итерации, предполагая известными поля температур T^(s+1) и функций тока ψ^(s+1);

6) находим максимальные относительные погрешности для разности полей искомых величин между (s) и (s + 1) итерациями по формулам:

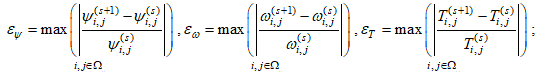       (31)

7) в том случае, если относительные погрешности, вычисленные по формулам (31), не превышают наперед заданной требуемой погрешности вычислений, то итерационный процесс останавливается, в противном случае увеличивается номер итерации s = s + 1 и осуществляется переход к пункту 3. 

Алгоритм численного интегрирования задачи

Движения частиц в движущейся жидкости под действием силы тяжести и градиента температуры

Осаждение частиц в поле тяжести в движущейся жидкости подразумевает учет влияния движения жидкости на перемещение осаждающихся в жидкости частиц. Как уже было сказано выше, движение жидкости оказывает влияние на движение осаждающихся частиц, в то время как обратного влияния движения частиц на движение жидкости не учитывается в виду малого размера и масс самих частиц.

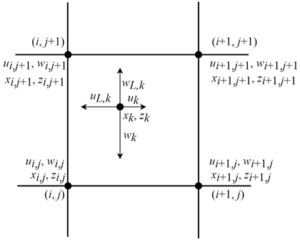
Влияние вклада движения жидкости на скорость движения частиц

Рассмотрим k-ую частицу в поле движения жидкости, находящуюся внутри сеточной области с индексами (i, j), (i+1, j), (i, j+1) и (i+1, j+1), рисунок рис. 3Рис. 3. На рисунке рис. 3 использованы следующие обозначения. Одиночным нижним индексом k описываются параметры частицы, ее координаты (x_k, z_k) и составляющие скорости (u_k, w_k). Двойные нижние индексы (i, j) использованы для описания узлов сетки, координат (x_i,j, z_i,j) и составляющих скоростей жидкости в узлах сетки (u_i,j, w_i,j). Одиночным нижним индексом k совместно с нижним индексом L обозначен вклад скорости движения жидкости в скорость движения частицы (u_L,k, w_L,k).

Рис. 3 – Частица с индексом k и скоростями (u_k и w_k) в поле движения жидкости, описываемом дискретным полем скоростей (u_i,j и w_i,j), и находящейся внутри сеточной ячейки с индексами (i, j), (i+1, j), (i, j+1) и (i+1, j+1)

 

Движение жидкости оказывает влияние на движение частиц только тем, что вносит вклад в изменение скорости движения частицы под влиянием движения жидкости. Следовательно, влияние движения жидкости на движение частицы в ней находящейся можно описать одним векторным уравнением для сложения скоростей:

     (32)

где за W_k^L обозначена скорость частицы в движущейся жидкости, W_k^L – скорость частицы в покоящейся жидкости, W_L,k – вклад движения жидкости в скорость движения частицы. Уравнение (32) в скалярной форме примет вид:

      (33)

Осталось вычислить вклад движения жидкости в скорость движения частицы по oz и oxy, как взвешенное среднее между скоростями в точках конечно-разностной сетки. После чего подправляются координаты частиц на текущем шаге интегрирования.

Корректировка поля температуры

Решение системы уравнений, описывающих движение жидкости в поле тяжести под действием перепада температур на верхней и нижней границе кюветы, дает распределение поля температур. Это поле температуры следует учитывать при расчете влияния броуновского движения жидкости на движение частиц, поскольку поле температур в каждой точке будет свое и уже не может быть описано линейной зависимостью. Для определения температуры вблизи k-ой частицы следует использовать значение полей температуры, которое будет вокруг k-ой частицы. Вычислить его можно используя средне взвешенные значения температуры.

Вычислительный алгоритм

Используются одинаковые характерные параметры задачи, выбранные для перевода задачи движения частиц и движения жидкости в безразмерную форму, – характерные размер (L₀), массу (M₀), время (T₀), и температуру (K₀), – для перевода уравнений движения частиц и движения жидкости в безразмерный вид. Задаются все параметры системы и определяются начальные условия.

Используя входные данные задачи, первоначально рассчитываются параметры движения жидкости, а именно функция тока, поле температур и поле вихря, определяется поле скоростей в жидкости. После этого начинается вычислительный цикл интегрирования по времени движения частиц.

На первом этапе положение и скорости частиц вычисляются согласно индивидуальным уравнениям движения каждой частицы (9), определяются положения частиц вдоль оси oz, которые описывают движения частиц без столкновений и теплового движения жидкости.

На втором шаге интегрирования пересчитываются скорости частиц под действием движения жидкости, подправляются координаты частиц.

На третьем шаге интегрирования пересчитываются скорости частиц под действием броуновского движения жидкости, подправляются координаты частиц.

На четвертом шаге интегрирования рассчитываются столкновения частиц в предположении, что одна частица может иметь только одно столкновение с другой на каждом этапе интегрирования. Подправляются скорости частиц и их координаты. После чего определяется величина рассеяния Рэлея по формуле (10).

На пятом шаге интегрирования пересчитываются скорости частиц под влиянием броуновского (теплового) движения жидкости, используя температуру жидкости вблизи частицы. Подправляются координаты всех частиц.

На шестом шаге этапе интегрирования рассчитываются столкновения частиц в предположении, что одна частица может иметь только одно столкновение с другой на каждом этапе интегрирования. Подправляются скорости частиц и их координаты.

На седьмом шаге определяется величина рассеяния Рэлея.

После чего процесс интегрирования уравнений движения частиц продолжается. Признаком окончания интегрирования являются выдвинутые критерии, которые обсуждаются в следующем разделе главы.

Модель определения массы частиц

Существуют два основных подхода к определению массы осаждаемых частиц. Первый из подходов к измерению массы частиц основан на анализе процесса и продолжительности осаждения частиц полимера и частиц наполнителя в жидкости. Второй подход основан на анализе минимального перепада температур в жидкости, который необходим для того, чтобы препятствовать процессу осаждения частиц. Следуя двум основным подходам к определению массы осаждаемых частиц, предлагаются две математических модели, которые описывают определение времени седиментации для первого подхода и вычисление минимальной температуры, достаточной для нахождения частиц во взвешенном состоянии для второго подхода. Общий характер кривых, описывающих общую площадь частиц обоих типов (полимера и наполнителя), перекрывающих лазерный луч, приведен на рисунке рис. 4.

Определение массы частиц по времени седиментации

Зависимость общей площади частиц, перекрывающих лазерный луч, от времени на рисунке рис. 4Рис. 5а приведена черной линией. Красной линией приведена площадь частиц наполнителя, а синей линией – площадь частиц полимера. Во вторых осях на рисунке рис. 4Рис. 5а точечной линией приведена скорость изменения общей площади частиц, перекрывающих лазерный луч в зависимости от времени. Абсолютные значения времени, площадей и скорости на рисунке рис. 4Рис. 5а не приведены, поскольку зависимости носят качественный вид.

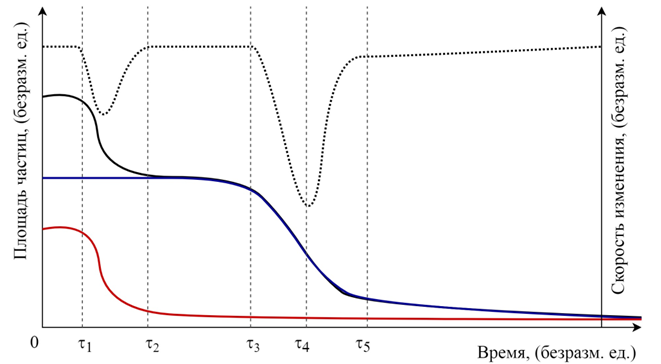
Рис. 4а – Зависимость площади частиц, перекрывающих лазерный луч, от времени без градиента температуры в жидкости: черная линия – общая площадь; красная линия – площадь частиц наполнителя, синяя линия – площадь частиц полимера. Во вторых осях точечной линией приведена скорость изменения общей площади частиц, перекрывающих лазерный луч в зависимости от времени

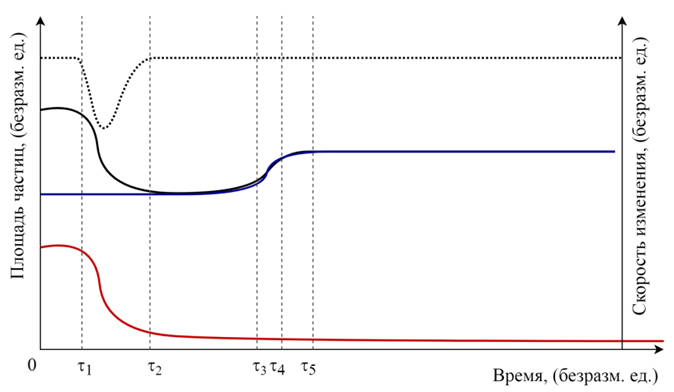
Рис. 5б – Зависимость площади частиц, перекрывающих лазерный луч, от времени с градиентом температуры в жидкости: черная линия – общая площадь; красная линия – площадь частиц наполнителя, синяя линия – площадь частиц полимера. Во вторых осях точечной линией приведена скорость изменения общей площади частиц, перекрывающих лазерный луч в зависимости от времени

 

Качественные зависимости показывают, что в начальный момент времени от нуля до τ₁ общая площадь частиц, перекрывающих лазерный луч, не меняется, поскольку тяжелые частицы, оседая, еще не дошли до верхнего края сечения луча. В период времени между τ₁ и τ₂ оседают тяжелые частицы наполнителя, проходя через круглое сечение лазерного луча. Перегиб кривой скорости осаждения (общей площади тяжелых частиц), между временами τ₁ и τ₂ как раз и вызван тем, что сечение лазерного луча круглое. Скорость изменения общей площади сначала невелика, потом достигает максимума и уменьшается после прохождения тяжелыми частицами центра лазерного луча. Плато между временами τ₂ и τ₃ свидетельствует о том, что легкие частицы в процессе своего осаждения еще не достигли верхнего края лазерного луча. В интервал времени между τ₃ и τ₅ происходит осаждение легких частиц полимера. Точка перегиба кривой осаждения в момент времени τ₄ свидетельствует о прохождении всеми легкими частицами середины лазерного луча. Время после τ₅ описывает плавное снижение концентрации частиц.

Временные интервалы, и взаимное отношение точек перегибов и относительных величин на кривых осаждения зависят не только от конкретно выбранных средних значений параметров частиц, но и от дисперсии их распределения. То, что кривые осаждения не доходят до нулевого значения, определяется наличием части сверхлегких частиц как первого, так и второго типов, ввиду дисперсии их масс. Ели дисперсия масс будет маленькой, то и кривые осаждения будут доходить до нуля.

Ключевой точкой по времени на кривой осаждения является время τ₄, которое свидетельствует о прохождении всеми легкими частицами середины лазерного луча. Используя значение этого времени, нетрудно вычислить массу частиц, поскольку будет известно расстояние ими пройденное от верхней части кюветы.

Для численного эксперимента легко вычислить время τ₄, определив второй минимум производной от зависимости общей площади частиц, перекрывающих лазерный луч, по времени. В численном эксперименте достаточно даже определить первый глобальный минимум производной от зависимости площади частиц полимера, перекрывающих лазерный луч, по времени. Для того, чтобы производная была достаточно гладкой, перед этим дискретная функция площади частиц полимера, перекрывающих лазерный луч, в зависимости от времени может быть сглажена методом скользящего среднего по формуле:

     (34)

где S_n – зависимость площади от дискретного времени в точках n×Δt, а p_k – весовые коэффициенты усреднения. Выбор окна усреднения и величин весовых коэффициентов усреднения следует осуществлять из общих рекомендаций к методам усреднения скользящим средним.

Производная этой зависимости определяется численно на основе конечных разностей по формуле:

    (35)

Критерий остановки вычислений по методу определения масс частиц на основе времени седиментации является найденный минимум производной, вычисленной по формуле (35).

Определение массы частиц по минимальному перепаду температур, достаточному для левитации частиц

Ячейки Бенара или, правильнее, ячейки Рэлея-Бенара – это возникновение упорядоченного движения жидкости в виде конвективных ячеек в форме цилиндрических валов или правильных шестигранных структур в слое вязкой жидкости с вертикальным градиентом температуры [8]. Управляющим параметром самоорганизации служит градиент температуры, вследствие которого в однородном слое жидкости начинается тепловая диффузия из-за возникающей неоднородности плотности жидкости. При увеличении градиента температуры возникает второй критический переход, при котором каждая ячейка распадается на две меньшего размера [8]. При увеличении температуры в жидкости возникает турбулентное движение, переходящее в хаотическое движение жидкости. При малом перепаде температур будет упорядоченное движение в виде двух встречно направленных ячеек Бенара.

В результате нагрева в жидкости будут образовываться восходящие и нисходящие потоки жидкости, которые будут увлекать в своем движении частицы полимера, в то время как тяжелые частицы наполнителя будут осаждаться. На рисунке рис. 4б приведена зависимость площади частиц, перекрывающих лазерный луч, от времени при градиенте температуры в жидкости. Черной линией на рисунке обозначена общая площадь частиц, красной линией – площадь частиц наполнителя, синей линией – площадь частиц полимера. Во вторых осях точечной линией приведена скорость изменения общей площади частиц, перекрывающих лазерный луч в зависимости от времени.

Та минимальная температура, которая необходима для поддержания частиц полимера во взвешенном состоянии в жидкости (после времени τ₅, рисунок рис. 4б), напрямую связана с массой частиц, которая и вызывает их осаждение.

Результаты моделирования, сравнение данных расчетов с данными эксперимента

Численный эксперимент был проведен для осаждения двух типов частиц, а именно оксида алюминия (Al₂O₃, наполнитель) и частиц полимера (легкие частицы), в этил ацетате, рисунок 5. Плотность этилацетата ρ_T1 = 902 кг/м³, коэффициент ее динамической вязкости μ = 0.40016×10^–3 Па×с. Средняя плотность частиц первого типа (Al₂O₃) ρ_T1 = 7987 кг/м³. Плотность частиц второго типа (полимер) ρ_T1 = 3000 кг/м³. Средний размер частиц наполнителя d_T1 = 0.25×10^–6 м, и полимера d_T1 = 0.125×10^–6 м. Число частиц наполнителя выбрано равным 1000, и полимера 10000.

 

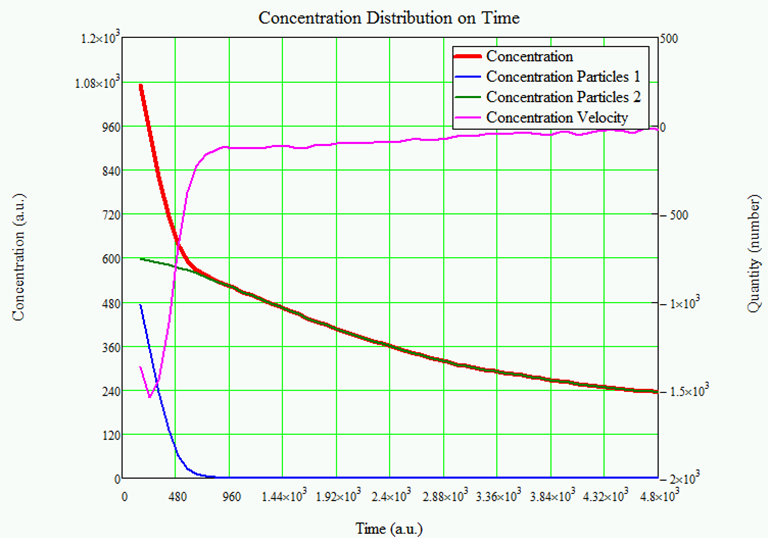
Рис. 5а – Изменение концентрации во времени: результаты математической модели: красная линия – общая концентрация; синяя линия – концентрация наполнителя; зеленая линия – концентрация полимера; фиолетовая линия – скорость изменения концентрации

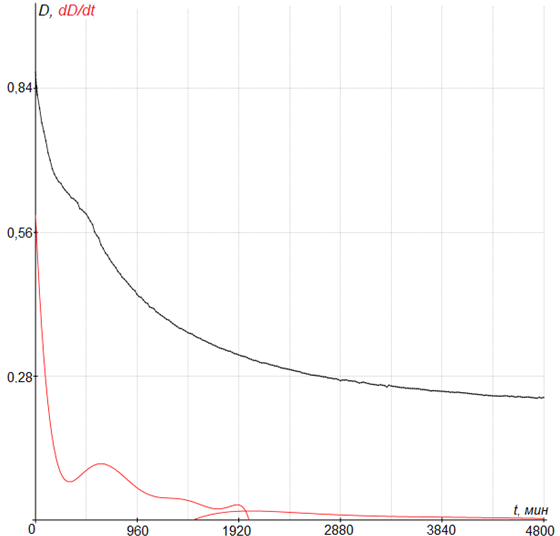
Рис. 5б – Изменение концентрации во времени: экспериментальные данные: черная линия – обычная концентрация; красная линия – скорость изменения концентрации

 

Как видно из изменения концентрации, показанной на рисунке 5, в начале процесса осаждение тяжелых частиц происходит вначале и очень быстро. После этого происходит осаждение легких частиц второго типа.

Заключение

Результатом построения математических моделей, предложенных в работе, явилось построение математической модели осаждения двух типов частиц в жидкости. Предложена полная двумерная математическая модель описания осаждения частиц в покоящейся жидкости. В математической модели учтено гауссово распределением размеров и плотностей частиц. Записаны уравнения движения частиц под действием сил тяжести, гидростатической выталкивающей силы Архимеда, силы сопротивления движению в вязкой жидкости при малых числах Рейнольдса. Предложена запись уравнений движения в безразмерной форме, удобной для их численного интегрирования. Произведен учет влияния броуновского движения молекул жидкости на скорость и перемещение осаждаемых частиц на основе модели упругого столкновения. Скорость броуновского движения молекул жидкости связана с температурой жидкости. Произведен учет неупругих столкновений частиц друг с другом, при котором частицы полностью слипаются, образуя новую частицу, с новой массой и скоростью. Смоделировано рассеяние Рэлея, возникающее при прохождении луча лазерного излучения через кварцевую кювету, содержащую раствор с осаждаемыми частицами. Предложен вычислительный алгоритм расчета величины рассеяния Рэлея в зависимости от осаждения частиц с течением времени.

Построена двумерная математическая модель движения жидкости в площади поперечного сечения лазерного луча под действием градиента температур между нижней и верхней поверхностями жидкости. Решена задача постановки граничных условий для системы уравнений в переменных функция тока, вихрь и температура. Предложен численный алгоритм решения системы уравнений движения жидкости, основанный на конечно-разностном подходе. Сформулированы граничные условия для конечно-разностной постановки. Предложен алгоритм решения каждого из системы уравнений движения жидкости, в конечно-разностной форме. Решена задача определения поля температур и поля скоростей в жидкости.

Предложена модель, объединяющая две математические модели движения частиц и движения жидкости, позволяющая учесть влияние движения жидкости под действием градиента температур на движение осаждаемых частиц, заключающаяся в учете влияния скорости жидкости на скорость осаждаемых частиц, в учете влияния поля температур.

Предложены две модели определения массы осаждаемых частиц, основанных на анализе продолжительности осаждения частиц полимера и частиц наполнителя в жидкости и на анализе минимального перепада температур в жидкости, который необходим для того, чтобы препятствовать процессу осаждения частиц.

Финансирование Работа выполнена при поддержке Минобрнауки России (соглашение номер 075-03-2020-051/3 от 09.06.2020, номер темы fzsu-2020-0021) в части постановки физической задачи моделирования, верификации данных и полученных результатов и Министерства науки и высшего образования Российской Федерации (соглашение номер 075-03-2020-051, номер тему fzsu-2020-0020) в части построения математической модели и её реализации.

Funding Funded by Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-03-2020-051/3, topic No. fzsu-2020-0021) in part of physical task formulation, data and results verification. Funded by Ministry of Science and Higher Education of the Russian Federation (Agreement No. 075-03-2020-051, topic No. fzsu-2020-0020) in part of mathematical model construction, training and tuning, and realization.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Ахмадеев А. А. Влияние толщины полимерной оболочки на поверхностях субмикронных частиц наполнителя на свойства полимерной композиции / А. А. Ахмадеев, Е. А. Богослов, М. П. Данилаев и др. // Механика композитных материалов. 2020. Т. 56. № 2. С.357.
2. Шилько С.В. Анализ механических свойств трансверсально-изотропных композитов с учетом межфазного слоя / С.В. Шилько, Ю.М. Плескачевский, С.В. Панин, Д.А. Черноус // Вестник национальной академии наук Белоруссии. №1. С.12.
3. Астафуров С.В. Исследование влияния свойств межфазных границ на механические характеристики металлокерамических композитов / С.В. Астафуров, Е.В. Шилько, В.Е. Овчаренко, С.Г. Псахье // Физическая мезомеханика. Т.17. № 3. С. 53.
4. Rajib Ghosh Chaudhuri Core/Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications / Rajib Ghosh Chaudhuri, Santanu Paria // Chem. Rev. 2012. V.112. № 4. P.2373.
5. Сахабутдинов Ж.М. Анализ дискретных моделей движения точки / Ж.М. Сахабутдинов. – Казань: ИММ РАН, 1995–196 с.
6. Кондратенко П.С. Теоретические основы гидродинамики и теплопереноса / П.С. Кондратенко. Москва: Институт проблем безопасного развития атомной энергетики РАН, 2003. 68 с.
7. Гидродинамика: учеб. Пособие для студентов нематематических факультетов / А.Б. Мазо, К.А. Поташев. – Казань: Казан. ун-т, 2013. – 2-е изд. – 128 с.
8. Ван-Дайк М. Альбом течений жидкости и газа / Ван-Дайк М. М.: Мир, 1986 – c. 84, рис. 139–140

Список литературы на английском языке / References in English

1. Akhmadeev A. A. Vlijanie tolshhiny polimernoj obolochki na poverhnostjah submikronnyh chastic napolnitelja na svojstva polimernoj kompozicii [Influence of the Thickness of the Polymer Enclosure on the Surfaces of Submicron Filler Particles on The Properties of the Polymer Composition] / A. A. Akhmadeev, E. A. Bogoslov, M. P. Danilaev et al. // Mehanika kompozitnyh materialov [Mechanics of Composite Materials]. 2020. Vol. 56. No. 2. p. 357. [in Russian]
2. Shilko S. V. Analiz mehanicheskih svojstv transversal'no-izotropnyh kompozitov s uchetom mezhfaznogo sloja [Analysis of Mechanical Properties of Transversally Isotropic Composites with Consideration of The Interfacial Layer]/ S. V. Shilko, Yu. M. Pleskachevsky, S. V. Panin et al. // Vestnik nacional'noj akademii nauk Belorussii [Bulletin of The National Academy of Sciences of Belarus]. 2014. No. 1. p. 12 [in Russian]
3. Astafurov S. V. Issledovanie vlijanija svojstv mezhfaznyh granic na mehanicheskie harakteristiki metallokeramicheskih kompozitov [Investigation of the Influence of the Properties of Interphase Boundaries on the Mechanical Characteristics of Metal-Ceramic Composites]/ S. V. Astafurov, E. V. Shilko, V. E. Ovcharenko et al. // Fizicheskaja mezomehanika [Physical Mesomechanics]. 2014. Vol. 17. No. 3, p. 53 [in Russian]
4. Rajib Ghosh Chaudhuri Core/Shell Nanoparticles: Classes, Properties, Synthesis Mechanisms, Characterization, and Applications // Chem. Rev. 2012. V.112. № 4. P.2373.
5. Sakhabutdinov Zh. M. Analiz diskretnyh modelej dvizhenija tochki [Analysis of Discrete Models of Point Motion]/ Zh. M. Sakhabutdinov. – Kazan: IMM RAS, 1995, 196 p.
6. Kondratenko P. S. Teoreticheskie osnovy gidrodinamiki i teploperenosa [Theoretical Foundations of Hydrodynamics and Heat Transfer]/ P. S. Kondratenko. M.: Institut problem bezopasnogo razvitija atomnoj jenergetiki RAN [Institute of Problems of Safe Development of Atomic Energy of The Russian Academy of Sciences], 2003, 68 p. [in Russian]
7. Gidrodinamika: ucheb. Posobie dlja studentov nematematicheskih fakul'tetov [Hydrodynamics: A Textbook for Students of Non-Mathematical Faculties] / A. B. Mazo, K. A. Potashev. - Kazan: Kazan. UN-t, 2013. - 2nd ed. - 128 p. [in Russian]
8. Van-Dyke M. Al'bom techenij zhidkosti i gaza [Album of Liquid and Gas Flows] / Van-Dyke M., Moscow: Mir, 1986, p. 84, fig. 139-140 [in Russian]