О ПРИБЛИЖЕННОМ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ФЕРХЮЛЬСТА ВТОРОГО ПОРЯДКА

О ПРИБЛИЖЕННОМ РЕШЕНИИ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ФЕРХЮЛЬСТА ВТОРОГО ПОРЯДКА

Научная статья

Михеев А.В. *

ORCID: 0000-0001-5953-0346,

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ», Санкт-Петербург, Россия

* Корреспондирующий автор (artem.v.miheev[at]gmail.com)

Аннотация

В данной работе рассматривается вопрос численного интегрирования дифференциального уравнения Ферхюльста второго порядка с заданными начальными условиями. Для этой цели используется два вида приближенных вычислений: расчёты в программе MathCAD (функция Odesolve) и представление решения в виде ряда Тейлора в окрестности точки, соответствующей начальным условиям. На основе рассматриваемого тестового примера проводится сравнение приближенных данных с точным решением уравнения. Полученные результаты представлены в аналитической и графической формах.

Ключевые слова: модель Ферхюльста, дифференциальные уравнения, динамические системы, численное моделирование. 

ABOUT APPROXIMATE SOLUTION OF THE SECOND ORDER FERHULST EQUATION

Research article

Mikheev A.V.*

ORCID: 0000-0001-5953-0346,

St. Petersburg State Electrotechnical University "LETI," St. Petersburg, Russia

* Corresponding author (artem.v.miheev[at]gmail.com)

Abstract

In this paper, the author considers the issue of numerical integration of the second-order Verhulst differential equation with given initial conditions. Two types of approximate calculations are used for this purpose: calculations in the MathCAD program (Odesolve function) and representing the solution as a Taylor series in a neighborhood of a point corresponding to the initial conditions. Based on the test case in question, approximate data are compared with the exact solution to the equation. The results are presented in analytical and graphical forms.

Keywords: Verhulst model, differential equations, dynamical systems, numerical simulation. 

Введение

Функция Ферхюльста была впервые предложена в работе [1] в качестве модели, описывающей процесс ограниченного экспоненциального роста. Данная модель находит широкое применение во множестве областей, таких как прикладная математика, биология, социология и т.д. Её общее представление имеет вид

    (1) В работе [2] были рассмотрены функции Ферхюльста вида     (2)

удовлетворяющие начальным условиям  и ограниченные сверху горизонтальной асимптотой . Функции  являются элементами фундаментальной системы решений (ФСР) линейного дифференциального уравнения (ЛДУ) второго порядка с переменными коэффициентами:

    (3) При этом коэффициенты  выражаются через функции ФСР согласно  формулам:     (4) где    (5)

В работе [3] автором была исследована зависимость частных решений уравнения (3) от вида начальных условий. Были обнаружены три вида решений: функции с двумя экстремумами, с одним экстремумом, а также монотонные функции.

Цель данной работы – рассмотреть два способа приближенного решения уравнения (3): при помощи разложения в степенной ряд по формуле Тейлора ([4]) и посредством функции Odesolve программного пакета MathCAD ([5]), а также сравнить полученные результаты с точным решением, представленным в виде линейной комбинации функций ФСР вида (2).

Численное интегрирование ЛДУ с помощью ряда Тейлора

Пусть имеется ЛДУ вида (3) с начальными условиями:

    (6)

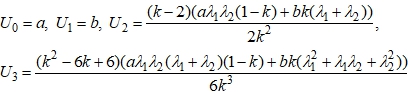Тогда его частное решение, соответствующее начальным условиям (6), может быть представлено в виде степенного ряда:     (7) где    (8) В дальнейших вычислениях мы ограничимся нахождением коэффициентов ряда (7) до третьей степени включительно. Из уравнения (3) и начальных условий (6) имеем:      (9) Из (4), (8), (9) мы получаем выражения для коэффициентов ряда (7) через параметры :     (10) Численное интегрирование ЛДУ в MathCAD

Для приближенного решения ЛДУ в Mathcad предусмотрена функция  Odesolve(t,p), t:=0,s..p где t – переменная, по которой производится интегрирование; p – верхняя граница, до которой проводится расчёт приближенного решения; s – шаг (расстояние между соседними точками, в которых находится значение решения). Начальные условия и само дифференциальное уравнение должны быть определены в блоке Given. На рисунке 1 приводится программный фрагмент, соответствующий решению уравнения (3) со следующими значениями:

   (11)

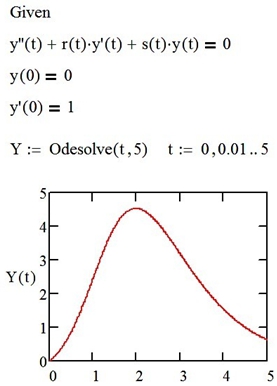
Рис. 1 – Приближенное решение уравнения Ферхюльста в пакете MathCAD

 

Сравнительный анализ

На рисунке 2 представлены графики точного решения (Z(t)) ЛДУ (3) со значениями параметров (11) и двух видов его приближенного решения: полученного интегрированием в MathCAD (Y(t)) и разложением в ряд Тейлора до третьей степени (U(t)). Как видно из графиков, между точным решением и приближенным решением в программе MathCAD не имеется значимых расхождений. Что касается ряда Тейлора, как и следовало ожидать, при возрастании параметра t мы наблюдаем существенное увеличение абсолютной погрешности AU(t) приближенного решения. Её зависимость от параметра t приводится на рисунке 3.

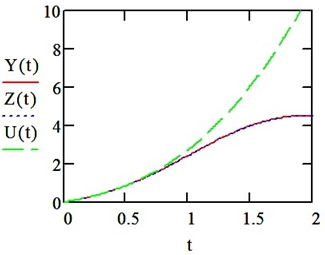
Рис. 2 – Графики точного и приближенного решений уравнения Ферхюльста

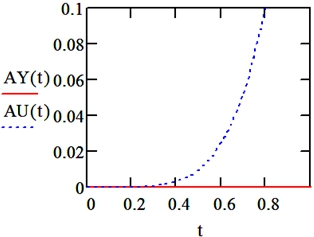
Рис. 3 – Графики абсолютной погрешности приближенных решений уравнения Ферхюльста по отношению к точному решению

  Заключение

Полученные результаты показывают, что приближенное решение в MathCAD для рассматриваемого типа уравнений является наиболее оптимальным с практической точки зрения. Недостатком данного способа решения является то обстоятельство, что пакет символьных вычислений MathCAD не позволяет получить требуемое решение в аналитической форме. Что касается использования разложения Тейлора, оно предоставляет требуемую точность лишь в малой окрестности точки начальных условий. Увеличение количества слагаемых, предоставляя лучшее приближение, позволяет повысить точность вычислений, однако из-за увеличения громоздкости выражения  в (10) с ростом числа слагаемых затрудняется получение общего аналитического выражения коэффициентов через параметры, участвующие в исходной задаче.

Конфликт интересов Не указан

Conflict of Interest None declared

Список литературы / References

1. Verhulst P. F. Notice sur la loi que la population suit dans son accroissement / P. F. Verhulst // Corresp. Math et Phys. – 1838. – №10. – P. 113–121.
2. Михеев А. В. О динамических моделях типа Ферхюльста, описываемых линейными дифференциальными уравнениями второго порядка / А. В. Михеев // Теория. Практика. Инновации. – 2017. – № 9 (21). – С. 29–33.
3. Михеев А. В. Исследование зависимости частных решений уравнения Ферхюльста второго порядка от начальных условий / А. В. Михеев // Теория. Практика. Инновации. – 2018. – № 8 (32). – С. 12–18.
4. Данилина Н. И. Вычислительная математика / Н. И. Данилина // – М. : Высшая школа, 1985. – 472 с.
5. Щенникова Е. В., Пучкова Е. Н. Вычислительный практикум в среде MathCAD / Е. В. Щенникова, Е. Н. Пучкова // – Саранск : ФГБОУ ВО "Национальный исследовательский Мордовский государственный университет им. Н. П. Огарева", 2010.

Список литературы на английском языке / References in English

1. Verhulst P. F. Notice sur la loi que la population suit dans son accroissement / P. F. Verhulst // Corresp. Math et Phys. – 1838. – №10. – 113–121.
2. Mikheev A. V. O dinamicheskih modelyah tipa Ferhyul'sta, opisyvaemyh linejnymi differencial'nymi uravneniyami vtorogo poryadka [On dynamic models of the verhulst type described by the second order linear differential equations] / A. V. Mikheev // Theory. Practice. Innovations. – 2017. – № 9 (21). – P. 29–33. [in Russian]
3. Mikheev A. V. Issledovanie zavisimosti chastnyh reshenij uravneniya Ferhyul'sta vtorogo poryadka ot nachal'nyh uslovij [The dependence of particular solutions of the second order verhulst equation from the initial conditions] / A. V. Mikheev // Theory. Practice. Innovations. – 2018. – № 8 (32). – 12–18. [in Russian]
4. Danilina N. I. Vychislitel'naya matematika [Computational mathematics] / N. I. Danilina, N. S. Dubrovskaya // – Moscow : High school, 1985. – 472 p. [in Russian]
5. Shennikova E. V. Vychislitel'nyj praktikum v srede MathCAD [Computing workshop in MathCAD environment] / E. V. Shennikova, E. N. Puchkova // – Saransk : FGBOU VPO "National Research Mordovian State University named after M.V. Lomonosov N. P. Ogarev", 2010. [in Russian]