АНАЛИЗ ТЕПЛОВЫХ СЕТЕЙ ЖКХ С ПОМОЩЬЮ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ

АНАЛИЗ ТЕПЛОВЫХ СЕТЕЙ ЖКХ С ПОМОЩЬЮ ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ

Научная статья

Баландин В.С.¹, Нешина Е.Г.^2, *, Дуйсенбаева М.С.³, Шайгараева Т.Н.⁴

¹ ORCID: 0000-0002-6593-1864;

² ORCID: 0000-0002-8973-2958;

³ ORCID: 0000-0003-3733-7662;

⁴ ORCID: 0000-0003-3324-133X;

^{1, 2, 3, 4} Карагандинский государственный технический университет, Караганда, Казахстан

* Корреспондирующий автор (1_neg[at]mail.ru)

Аннотация

В данной статье авторы проводят анализ тепловых сетей ЖКХ. Применяя теорию массового обслуживания, проводят оценку работоспособности системы при определенных заданных критериях и поиском оптимальных характеристик работы системы. Наиболее ответственными элементами распределения тепла к потребителю являются трубы, которые должны быть достаточно прочными и герметичными при максимальных давлениях и температурах теплоносителя. Авторами рассмотрен вопрос о возможности расчета плановой себестоимости услуг оператора ТС, у которого объемы услуг определяются исходя из пропускной возможности ЦТП.

Ключевые слова: тепловые сети, тепловая энергия, центральный тепловой пункт, теплоснабжение, массовое облуживание, температура.

ANALYSIS OF HOUSING HEAT NETWORKS WITH THE USE OF MASS SERVICE THEORY

Research article

Balandin V.S.¹, Neshina E.G.^2, *, Duisenbaeva M.S.³, Shaigaraeva T.N.⁴

¹ ORCID: 0000-0002-6593-1864;

² ORCID: 0000-0002-8973-2958;

³ ORCID: 0000-0003-3733-7662;

⁴ ORCID: 0000-0003-3324-133X;

^{1, 2, 3, 4} Karaganda State Technical University, Karaganda, Kazakhstan

* Corresponding author (1_neg[at]mail.ru)

Abstract

The authors analyze the heating networks of housing and communal services in the paper. Applying the queuing theory, the assessment of the system’s performance under certain specified criteria is made by searching for optimal system performance. The most critical elements of heat distribution to the consumer are pipes, which should be sufficiently strong and tight at maximum pressures and temperatures of the coolant. The authors considered the question of the possibility of calculating the planned cost of services of a vehicle operator, in which the volume of services is determined based on the capacity of the central heating center.

Keywords: heat networks, heat energy, central heat point, heat supply, mass tinning, temperature.

Введение

Выбор форм представления математических моделей и эффективности численных методов их решения для применения в практических приложениях является актуальным.

В конечном итоге, функционирование тепловых сетей, как и любого предприятия, определяется ее экономической эффективностью. Поэтому построенная модель тепловых сетей должна удовлетворять принципам экономической целесообразности.

Перечисленные выше проблемы характерны для большинства коммуникационных систем, включая системы теплоснабжения. Единого алгоритма их решения не существует, поэтому многие исследователи идут по пути использования тех или иных моделей для построения отдельных сторон процесса функционирования тепловых сетей.

Анализ тепловых сетей проводился на основе тепловых сетей города Абай Карагандинской области.

Источником теплоснабжения потребителей жилого массива и промышленных район г. Абай является ГРЭС ТОО «Корпорация Казахмыс». расположенная в поселке Топар.

Максимальная температура сетевой воды при расходе 2200 т/ч = 960 С.

Трубопроводы тепломагистралей проложены надземным способом, в основном на низких опорах. Компенсация тепловых удлинений трубопроводов осуществляется П- разными и сальниковыми компенсаторами, а также за счет переходов через дороги и поворотов теплотрассы.

Состояние теплоизоляции трубопроводов, в основном, удовлетворительное, но имеются участки с полным отсутствием и теплоизоляции, и покровного слоя.

Внутриквартальные тепловые сети - двухтрубные, радиальные, тупиковые. Тип прокладки трубопроводов тепловых сетей в черте города смешанный - надземный и подземный. Суммарная расчетная тепловая нагрузка потребителей тепла г. Абая составляет 50,202 Гкал/ч.

Тепловые сети в виду их направленности будут определяться как система с массовым облуживанием. Взаимодействия различных элементов системы теплоснабжения должно достигаться за счет достижения оптимальных параметров работы при максимальной эффективности, повышения надежности работы  и снижения частоты отказов. Одной из составных частей тепловой сети является центральный тепловой пункт [1], [2].

Центральный тепловой пункт (ЦТП) – устройство для присоединения систем теплоснабжения части населённого пункта к распределительным сетям города или области.

Теория массового обслуживания оценивает работоспособность при определенных заданных критериях и поиском оптимальных характеристик работы. Оптимальные характеристики позволяют обеспечивать надлежащее качество сервиса при минимальных затратах и достигать устойчивой работы в различных сценариях работы в период отопительного сезона в зависимости от климатических условий, условий работы, амортизации и технического отслеживания состояния оборудования.

Структура системы показана на рисунке 1.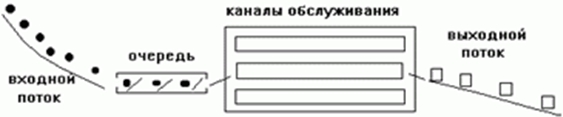  

Рис. 1 – Элементы системы массового обслуживания

 

В качестве входного потока служат абоненты, ждущие получение той или иной услуги (теплоснабжения или горячего водоснабжения), создается очереди из этих абонентов, каналами обслуживаниями служат теплоснабжающие организации, который формируют задачи в выходном потоке.

Рассмотрим систему массового обслуживания с ограничением длины очереди. Если длина становится равной m, то очередное требование теряется. Запишем систему дифференциальных уравнений, описывающих работу такой системы массового обслуживания. Вероятность n+m-го состояния определяется из уравнения:

    (1)

Система дифференциальных уравнений (1) при k=n+m определяет вероятности состояний для системы массового обслуживания с ограниченной очередью.

Предельные значения вероятностей состояний (при t→∞) находятся из системы алгебраических линейных уравнений:

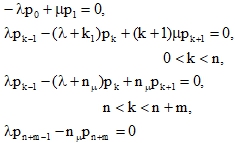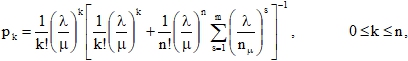    (2) с условием:      (3) Из этих уравнений получаем:     (4)

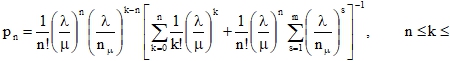
Один ЦТП может обслуживать n абонентов. Взяв за основу текущую обеспеченность ресурсами оператором ТС, и опираясь на существующие нормативы, исходя из возможности оказания услуг оператором ТС по ЦТП i, рассчитываем среднее число абонентов, приходящихся на один ЦТП:

    (5) где m_i – число ЦТП, t₁ – число часов в году, t₂ – продолжительность рабочего дня, t₃ – среднее время использования ЦТП абонентом.

От выражения (5) перейдем к следующему равенству:

    (6)

Отношение в левой части равенства является, фактически, средней интенсивностью потока заявок в СМО, в дальнейшем станем обозначать его через λ. Отношение в правой части равенства представляет собой интенсивность обслуживания, в дальнейшем обозначаемую через μ, при выполнении условия:

    (7)

где ρ –коэффициент загрузки системы, система работает в стационарном режиме.

В стационарном режиме интенсивность потока уходящих заявок равна λ. Коэффициент загрузки ρ в стационарном режиме есть:

а) среднее значение той части единицы времени, в течение которой ЦТП занят;

б) вероятность того, что ЦТП занят;

в) среднее число заявок в ЦТП.

Записанное выше можно расценивать, что механизм ТС, как система массового обслуживания.

Для λ имеет смысл данная формула:

    (8)

где n – число заявок, т.е. мы рассматриваем в нашем случае каждого абонента как источник n заявок, которые могут занимать систему.

Для многоканальной исследуемой системы:

    (9)

Т₀ – среднее время обслуживания канала, или 1/μ. Его значение также должно удовлетворять выражению стационарности.

Длина очереди данной системы:

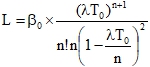    (10)

где β₀ – стационарная вероятность того, что в исследуемой системе нет заявок. Эта вероятность определяется в виде:

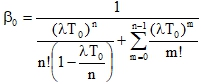    (11) Варьируя численность абонентов в системе, мы получаем закон распределения длины очереди (см. рисунок 1.2).  

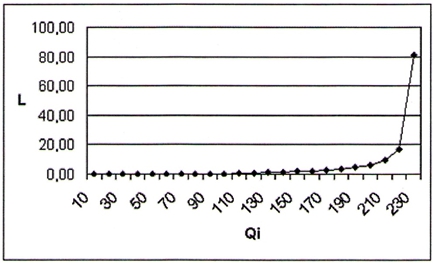
Рис. 2 – Зависимость средней длины очереди L в теплоснабжающей организации от количества абонентов

  Заключение

В рамках теории массового обслуживания рассмотрен вопрос о возможности расчета плановой себестоимости услуг оператора, у которого объемы услуг определяются исходя из пропускной возможности ЦТП. Показано, что использование методов теории массового обслуживания в маркетинговых исследованиях в области теплоэнергетики выглядит достаточно целесообразным. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Саати T.Л. Элементы теории массового обслуживания и ее приложения / Саати T.Л. - M.: Сов. радио, 2005. – 346 с.
2. Хинчин A.Я. Работы по теории массового обслуживания Хинчин A.Я. - M.: Физматгиз, 2013. – 542 с.
3. Новиков Ф. Дискретная математика для программистов / Новиков Ф. – СПб: Питер, 2001. – 301 с.
4. Иванов Б.Н. Дискретная математика. Алгоритмы и программы./ Иванов Б.Н. – М.; Лаборатория Базовых Знаний, 2002. - 288 с.
5. Том Р. Структурная устойчивость и морфогенез Том Р. - М.: Логос, 2002. – 232 с.
6. Дуброва Т.А. Статистические методы прогнозирования / Дуброва Т.А. - М.: МЭСИ, 2004. – 182 с.
7. Лукашин Ю.П. Адаптивные методы прогнозирования временных рядов / Лукашин Ю.П. – М.: Финансы и статистика, 2003. – 212 с.
8. Дуброва Т.А. Корреляционно-регрессионный анализ в системе Statistica / Дуброва Т.А., Павлов Д.Э., Ткачев О.В. - М.: МЭСИ, 1999. – 162 с.
9. Афанасьев В.И. Анализ временных рядов и прогнозирование / Афанасьев В.И., Юзбашев М.М. - М.: Финансы и статистика, 2001. – 194 с.
10. Дуброва Т.А. Статистические методы прогнозирования / Дуброва Т.А. - М.: ЮНИТИ-ДАНА, 2003. – 186 с.

Список литературы на английском языке / References in English

1. Saati T. L. Elementy teorii massovogo obsluzhivaniya i yeye prilozheniya [Elements of the theory of queuing and its applications] / Saati T. L. – M.: Sov. Radio, 2005. – 346 p. [in Russian]
2. Khinchin A.Ya. Raboty po teorii massovogo obsluzhivaniya [Works on theory of queuing] / Khinchin A.Ya.– M.: Fizmatgiz, 2013. – 542 p. [in Russian]
3. Novikov F. Diskretnaya matematika dlya programmistov [Discrete mathematics for programmers] / Novikov F. – St. Petersburg: Peter, 2001. – 301 p. [in Russian]
4. Ivanov B.N. Diskretnaya matematika. Algoritmy i programmy [Discrete Math. Algorithms and programs] / Ivanov B.N.– M.; Laboratory of Basic Knowledge, 2002. – 288 p. [in Russian]
5. Tom R. Strukturnaya ustoychivost' i morfogenez [Structural stability and morphogenesis] / Tom R. – M.: Logos, 2002. – 232 p. [in Russian]
6. Dubrova T.A. Statisticheskiye metody prognozirovaniya [Statistical forecasting methods] / Dubrova T.A – M.: MESI, 2004. – 182 p. [in Russian]
7. Lukashin Yu.P. Adaptivnyye metody prognozirovaniya vremennykh ryadov [Adaptive methods of forecasting time series.] / Lukashin Yu.P.– M.: Finance and Statistics, 2003. – 212 p. [in Russian]
8. Dubrova T.A. Korrelyatsionno-regressionnyy analiz v sisteme Statistica [Correlation and regression analysis in Statistica system] / Dubrova T.A., Pavlov D.E., Tkachev O.V. – M.: MESI, 1999. – 162 p. [in Russian]
9. Afanasyev V.I. Analiz vremennykh ryadov i prognozirovaniye [Time Series Analysis and Forecasting] / Afanasyev V.I., Yuzbashev M.M. – M.: Finance and Statistics, 2001. – 194 p. [in Russian]
10. Dubrova T.A. Statisticheskiye metody prognozirovaniya [Statistical forecasting methods] / Dubrova T.A.  – M.: UNITY-DANA, 2003. – 186 p. [in Russian]