РЕШЕНИЕ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ СИНТЕЗА С ИСПОЛЬЗОВАНИЕМ ЛОГИКО-КОМБИНАТОРНОГО ПОДХОДА
Белозеров А.Л.
Аспирант, Санкт – Петербургский горный университет
РЕШЕНИЕ МНОГОКРИТЕРИАЛЬНЫХ ЗАДАЧ СИНТЕЗА С ИСПОЛЬЗОВАНИЕМ ЛОГИКО-КОМБИНАТОРНОГО ПОДХОДА
Аннотация
В статье рассматривается решение многокритериальных задач структурного синтеза, в которых формирование множества возможных решений осуществляется на основе логико-комбинаторного подхода. Множество вариантов задается в рамках парадигмы онтологического инжиниринга и иерархического морфологического подхода - системой логических уравнений на двух уровнях: на уровне базовых функций и на уровне экземпляров базовых функций. Целевая функция формируется как свертка частных показателей на основе взвешенного степенного среднего. Приводится базовый алгоритм минимизации решений с аддитивными показателями на особенных скобочных формах.
Ключевые слова: логико-комбинаторный подход, иерархический морфологический подход, взвешенное степенное среднее.
Belozerov A.L.
Postgraduate student, Saint – Petersburg Mining University
SOLUTIONS OF MULTICRITERIA PROBLEMS SYNTHESIS USING LOGIC-COMBINATORIAL APPROACH
Abstract
The paper deals with the synthesis of multiobjective structural problems, in which the formation of a set of possible solutions is based on the logic-combinatorial approach. Plenty of options given in the framework of the paradigm of the ontological engineering and hierarchical morphological approach - a system of logical equations at two levels: at the level of the basic functions on the level instances of the basic functions. The objective function is formed as a convolution of particular indicators based on the weighted average power. We present the basic algorithm to minimize additive solutions with performance on special bracket form.
Keywords: logical-combinatorial approach, hierarchical morphological approach, the average weighted degree.
В статье рассматривается решение многокритериальных задач структурного синтеза (дискретного программирования), в которых формирование множества возможных решений осуществляется на основе логико-комбинаторного подхода (ЛКП) [1, 3, 5]. Под многокритериальным синтезом понимают формирование множества альтернативных вариантов структуры синтезируемого объекта, так и выбор оптимального варианта структуры. В задачах управления и проектирования синтезируемый объект рассматривается как система, взаимодействующая с внешней средой (надсистемой), причем под структурой системы обычно понимают состав элементов и подсистем рассматриваемой системы, закрепление определенных функций за элементами и подсистемами, а также организацию связей и отношений между подсистемами, элементами и внешней средой. Множество вариантов задается в рамках парадигмы онтологического инжиниринга и иерархического морфологического подхода (ИМП) - системой логических уравнений на двух уровнях: на уровне базовых функций и на уровне экземпляров базовых функций. Целевая функция формируется как свертка частных показателей на основе взвешенного степенного среднего (ВСС) [4,6].
Методы синтеза модульного оборудования отличаются от традиционных методов ориентированностью на широкое применение компьютерных технологий. Модульный синтез понимается как синтез возможных компоновок модульной системы из заданного набора модулей и анализ их свойств. Исходными данными для синтеза служат множество модулей и отношение агрегируемости, определяющее стыкуемость модулей. Процедуры синтеза продуцируют, вообще говоря, некоторое множество компоновок, удовлетворяющих заданным функциональным требованиям, но отличающихся структурой и составом модулей и, в силу этого, имеющих различные технические и экономические характеристики. Некоторые из этих характеристик имеют системный характер и могут быть получены только в результате экспериментальных исследований или имитационного моделирования [9].
Предполагаем, что синтезируемый объект характеризуется составом базовых функций (БФ). Если имеется один вариант состава БФ, то множество возможных решений задается классической МТ. Например, в задаче синтеза системного блока ПЭВМ, состоящего из системного блока (SysBloc), корпуса (Korp), блока питания (BlocPit) и материнской платы (MatPlata), включающей процессор (Proc) и оперативную память (OpMem), множество V возможных решений задается различными вариантами реализации четырех базовых функций Korp, BlocPit, Proc и OpMem. В общем случае m базовых функций, это множество задается декартовым произведением:
![]() (1)
(1)
где ![]() - множество вариантов реализации (экземпляров) j-й базовой функции,
- множество вариантов реализации (экземпляров) j-й базовой функции, ![]() - элемент, реализующий k-й вариант базовой функции j. Каждый вариант -
- элемент, реализующий k-й вариант базовой функции j. Каждый вариант - ![]() . В еще более общем случае, когда множество V задается в виде ОСФ, а структурные варианты могут различаться составом базовых функций, мы вводим функцию
. В еще более общем случае, когда множество V задается в виде ОСФ, а структурные варианты могут различаться составом базовых функций, мы вводим функцию ![]() , отображающую множество элементов Z в множество базовых функций F.
, отображающую множество элементов Z в множество базовых функций F.
Целевая функция основана на n показателях ![]() , причем показатели
, причем показатели ![]() являются аддитивными, а показатель
являются аддитивными, а показатель ![]() - максиминным. Аддитивные показатели - это минимизируемые показатели (стоимость, масса, интенсивность отказов и т.д.). Значение i -го аддитивного показателя для варианта
- максиминным. Аддитивные показатели - это минимизируемые показатели (стоимость, масса, интенсивность отказов и т.д.). Значение i -го аддитивного показателя для варианта ![]() вычисляется по формуле
вычисляется по формуле
![]() (2)
(2)
где ![]() - значение i -го аддитивного показателя элемента
- значение i -го аддитивного показателя элемента ![]() .
.
Максиминный показатель ![]() обеспечивает приближенную оценку технического совершенства варианта
обеспечивает приближенную оценку технического совершенства варианта ![]() следующим образом. Предполагается, что каждый элемент
следующим образом. Предполагается, что каждый элемент ![]() варианта
варианта ![]() характеризуется показателем технического совершенства
характеризуется показателем технического совершенства ![]() , который должен быть не хуже заданного, определяемого на основе опыта, предварительных исследований и т.д. Например, для системного блока ПЭВМ - блок питания должен обеспечивать мощность не меньше заданной, процессор - быстродействие не меньше заданного, оперативная память - объем не меньше заданного и т.д. Это позволяет решить проблему построения параметрических моделей в случае их разнородности [5] для всего множества V возможных решений задачи структурного синтеза.
, который должен быть не хуже заданного, определяемого на основе опыта, предварительных исследований и т.д. Например, для системного блока ПЭВМ - блок питания должен обеспечивать мощность не меньше заданной, процессор - быстродействие не меньше заданного, оперативная память - объем не меньше заданного и т.д. Это позволяет решить проблему построения параметрических моделей в случае их разнородности [5] для всего множества V возможных решений задачи структурного синтеза.
В качестве целевой функции, характеризующей технико-экономическое совершенство синтезируемого объекта, мы используем максимизируемую на V свертку в форме ВСС [4,7]:
![]() (3)
(3)
где yi - нормированное значение и ![]() - вес i-го показателя, r - степень ВСС. Смысл использования (3) в качестве максимизируемой целевой функции основан в том, что
- вес i-го показателя, r - степень ВСС. Смысл использования (3) в качестве максимизируемой целевой функции основан в том, что ![]() при
при ![]() . Благодаря этому, при значениях
. Благодаря этому, при значениях ![]() >1, мы отдаем предпочтение, и в тем большей степени, чем больше
>1, мы отдаем предпочтение, и в тем большей степени, чем больше ![]() , вариантам
, вариантам ![]() , которые имеют наилучшее значение наихудшего показателя (максимин). Тем самым обеспечивается гармонизация [2] показателей синтезируемого объекта.
, которые имеют наилучшее значение наихудшего показателя (максимин). Тем самым обеспечивается гармонизация [2] показателей синтезируемого объекта.
Аддитивные минимизируемые показатели (стоимость, масса, интенсивность отказов и т.д.) для каждого варианта ![]() нормируются относительно соответствующего целевого (эталонного) значения
нормируются относительно соответствующего целевого (эталонного) значения ![]() так, что их нормированные значения становятся максимизируемыми:
так, что их нормированные значения становятся максимизируемыми:
![]() (4)
(4)
где ![]() вычисляется по формуле (2).
вычисляется по формуле (2).
Нормированный максиминный показатель ![]() для каждого варианта
для каждого варианта ![]() получается взятием минимума
получается взятием минимума
![]() (5)
(5)
где ![]() - нормированное значение максиминного показателя элемента
- нормированное значение максиминного показателя элемента ![]() . Если
. Если ![]() -максимизируемый показатель, то вычисляется по формуле
-максимизируемый показатель, то вычисляется по формуле
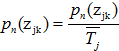 (6)
(6)
где ![]() - целевое значение для j-й БФ. Если среди показателей
- целевое значение для j-й БФ. Если среди показателей ![]() , имеются минимизируемые, то вместо (6) следует использовать формулу
, имеются минимизируемые, то вместо (6) следует использовать формулу ![]()
В базовом алгоритме минимизации на ОСФ, а именно, реализуется поиск варианта ![]() , доставляющего
, доставляющего
![]() (7)
(7)
для n нормированных аддитивных показателей ![]() , где - выбираемые пользователем весовые коэффициенты, причем
, где - выбираемые пользователем весовые коэффициенты, причем ![]() . Пользователь использует эти весовые коэффициенты для того, чтобы найти наилучшую точку на выпуклой оболочке множества Парето. Дополнительное обоснование можно найти в [5, 8].
. Пользователь использует эти весовые коэффициенты для того, чтобы найти наилучшую точку на выпуклой оболочке множества Парето. Дополнительное обоснование можно найти в [5, 8].
Базовый алгоритм программы основан на том, что вычисление нормированных значений для минимизируемых аддитивных показателей ![]() , используемых в формуле (7), выполняется по формуле:
, используемых в формуле (7), выполняется по формуле:
![]() (8)
(8)
Очевидно, что для ![]()
![]() (9)
(9)
где ![]() - нормированный аддитивный показатель элемента
- нормированный аддитивный показатель элемента ![]() , который желательно минимизировать, вычисляется по формуле:
, который желательно минимизировать, вычисляется по формуле:
![]() (10)
(10)
- это аддитивный вклад элемента ![]() в целевую функцию (7) по всем показателям
в целевую функцию (7) по всем показателям ![]() с учетом весовых коэффициентов
с учетом весовых коэффициентов ![]() . Остается получить формулу для
. Остается получить формулу для ![]() , т.е. для максиминных показателей.
, т.е. для максиминных показателей.
Реализация (7) для максиминных показателей основана на их аддитивной аппроксимации. Максимизацию выражения (5) ![]() , можно заменить на максимизацию приближенного значения минимума, вычисляемого на основе ВСС
, можно заменить на максимизацию приближенного значения минимума, вычисляемого на основе ВСС
![]() (13)
(13)
где ![]() - это нормированный аддитивный вклад минимаксного показателя
- это нормированный аддитивный вклад минимаксного показателя ![]() в целевую функцию (7):
в целевую функцию (7):
![]() (15)
(15)
Таким образом, представление множества возможных решений V в виде ОСФ1 или ОСФ2 [3, 5] позволяет найти глобальный минимум и некоторое подмножество Vs субоптимальных решений для (7) за счет отбора в каждой дизъюнкции элементов ![]() , обеспечивающих локальный минимум
, обеспечивающих локальный минимум ![]() и близкие к нему значения. Оптимальное решение относительно целевой функции (3) получается путем подбора пользователем весовых коэффициентов
и близкие к нему значения. Оптимальное решение относительно целевой функции (3) получается путем подбора пользователем весовых коэффициентов ![]() и перебора на подмножестве Vs.Практический пример применения решения будет рассмотрен в следующей статье.
и перебора на подмножестве Vs.Практический пример применения решения будет рассмотрен в следующей статье.
Список литературы / References
- Анкудинов Г.И. Об одном общем подходе к свертыванию частных критериев эффективности // Автоматизированные системы управления.- Л.: ЛГУ, 1974.- Вып.1.- С.39-41.
- Богданов А.А. Тектология: Всеобщая организационная наука.- М.: Финансы, 2003.- 496 с.
- Анкудинов Г.И. Синтез структуры сложных объектов.- Л.: ЛГУ, 1986.- 260 с.
- Анкудинов Г.И., Анкудинов И.Г. Нелинейная свертка частных критериев на основе интервальных оценок // Материалы научной конференции. Часть 1.- СПб.: СЗТУ, 2003.- С. 136139.
- Анкудинов И.Г. Автоматизация структурного синтеза и принятия решений в управлении и проектировании.- СПб.: Изд-во Политехн. ун-та, 2008.- 202 с.
- Анкудинов Г.И, Анкудинов И.Г. Гармонизация иерархий на основе взвешенного степенного среднего // «Управление развитием крупномасштабных систем (MLSD’2012)». VI международная конференция, 1-3 октября 2012 г., Москва. - Материалы: в 2-х т.- 1 т.- С. 139.
- Анкудинов Г.И, Анкудинов И.Г. Мультикритериальный выбор решений на основе предельных уступок и коэффициентов замещения показателей // Записки Горного института, СПб, 2014, Т. 208. С. 208-215.
- Ногин В.Д. Принятие решений при многих критериях. Учебнометодическое пособие.- СПб. Издательство «ЮТАС», 2007. - 104 с.
- Рябов О. Н. Модели и методы автоматизированного синтеза сборочных комплексов модульной структуры для приборостроения: автореф дис. канд. технических наук ГОУ ВПО «Саратовский государственный технический университет», Саратов, 2006.
Список литературы на английском языке / References in English
- Ankudinov G.I, Ob odnom obshhem podhode k svertyvaniju chastnyh kriteriev jeffektivnosti [A general approach to curtailing private performance criteria] // Avtomatizirovannye sistemy upravlenija [Automated control systems].- : LGU, 1974.- Edition.1.- P.39-41. [in Russian]
- Bogdanov A.A. Tektologija: Vseobshhaja organizacionnaja nauka. [Tectology: Universal organizational science] - M.: Finansy, 2003.- 496 p. [in Russian]
- Ankudinov G.I. Sintez struktury slozhnyh ob#ektov. [The synthesis of the structure of complex objects.] – L.: LGU, 1986.– 260 s. [in Russian]
- Ankudinov G.I, Ankudinov I.G Nelinejnaja svertka chastnyh kriteriev na osnove interval'nyh ocenok [Nonlinear convolution of partial criteria on the basis of interval estimates] // Materials of scientific conference. Part 1.- SPb.: SZTU, 2003.- P. 136139. [in Russian]
- Ankudinov I.G. Avtomatizacija strukturnogo sinteza i prinjatija reshenij v upravlenii i proektirovanii [Automation of structural synthesis and decision-making in the management and design].- SPb.: publishing Polytechnic University, 2008.- 202 p. [in Russian]
- Ankudinov G.I, Ankudinov I.G. Garmonizacija ierarhij na osnove vzveshennogo stepennogo srednego [Harmonisation of hierarchies on the basis of the weighted average power] // «Upravlenie razvitiem krupnomasshtabnyh sistem [Management of development of large scale systems] (MLSD’2012)». VI international conference, 1-3 october 2012, Moscow. − in the 2nd v. − 1 v. − P. 139. [in Russian]
- Ankudinov G.I, Ankudinov I.G. Mul'tikriterial'nyj vybor reshenij na osnove predel'nyh ustupok i kojefficientov zameshhenija pokazatelej [Multicriteria selection decisions on the basis of marginal concessions and performance of replacement rates] // Zapiski Gornogo instituta, SPb, 2014, V. 208. P. 208-215. [in Russian]
- Nogin V.D. Prinjatie reshenij pri mnogih kriterijah. [Decision-making in many criteria.] Textbook.- SPb. publishing house «JuTAS», 2007. - 104 p. [in Russian]
- Rjabov O. N. Modeli i metody avtomatizirovannogo sinteza sborochnyh kompleksov modul'noj struktury dlja priborostroenija [Models and methods of the automated synthesis of assembly complexes of modular structure for instrument making]: PhD dissertation, GOU VPO «Saratovskij gosudarstvennyj tehnicheskij universitet», Saratov, 2006. [in Russian]
