РАСЧЕТ СИСТЕМЫ ПРИВОДА: ПРУЖИНА ИЗ МАТЕРИАЛА С ЭФФЕКТОМ ПАМЯТИ ФОРМЫ – КОНТРПРУЖИНА

Летенков О.В.¹, Филиппов Д.А.²

¹ORCID: 0000-0001-5315-5659, Кандидат технических наук, ²ORCID: 0000-0002-4359-7770, Доктор физико-математических наук, Новгородский государственный университет имени Ярослава Мудрого

Работа выполнена при поддержке Министерства образования и науки РФ в рамках проектной части государственного задания, проект № 177

РАСЧЕТ СИСТЕМЫ ПРИВОДА: ПРУЖИНА ИЗ МАТЕРИАЛА С ЭФФЕКТОМ ПАМЯТИ ФОРМЫ – КОНТРПРУЖИНА

Аннотация

В статье предложен метод расчета привода системы, состоящей из термочувствительного элемента, изготовленного из материала с эффектом памяти формы и упругого контртела, выполненных в виде пружин сжатия. Данная система может быть использована в качестве рабочих элементов в механизмах поступательного движения. При расчете использовались следующие параметры системы: жесткость пружины из материала с эффектом памяти формы в „низкотемпературном” (мартенситном) и „горячем” (аустенитном) состояниях, жесткость упругой контрпружины, величина предварительной усадки привода и величина рабочего хода исполнительного звена при термоциклировании привода через температурный интервал мартенситного превращения. Показано, что варьирование отдельно взятыми величинами предварительной осадки термочувствительной пружины или контрпружины, дает возможность управлять не только  величиной рабочего хода, но и температурой начала движения исполнительного звена.

Ключевые слова: эффект памяти формы, мартенситный переход, упругий элемент, контртело.

Letenkov O.V.¹, Filippov D.A.²

¹ORCID: 0000-0001-5315-5659, PhD in Engineering, ²ORCID: 0000-0002-4359-7770, PhD in Physical and Mathematical Sciences,  Yharoslav-the-Wise Novgorod State University

CALCULATION OF THE SYSTEM DRIVE: SPRING FROM MATERIAL WITH SHAPE MEMORY EFFECT – COUNTER SPRING

Abstract

Method for calculating a drive system consisting of a heat-sensitive element made of a material with shape memory effect and a elastic opposing member made in the form of compression springs is presented. This system can be used as working elements in the translational motion mechanisms. At the calculation was used the following system parameters: the stiffness of the material of the spring with shape memory in the "low temperature" (martensitic) and "hot" (austenitic) states, the hardness of elastic counter spring, the magnitude of the drive pre-shrinkage and the amount of stroke actuator when the drive system make the cyclical transitions through the temperature martensitic transformation range. It is shown that the variation of individual values SME of pre-precipitation heat-sensitive spring or counter spring, makes it possible to control not only the magnitude of the stroke, but also the temperature of the beginning of the movement of an actuator.

Keywords: shape memory effect, martensitic transition, elastic member,  counter spring

Введение

Материалы с эффектом памяти формы (ЭПФ) – это материалы, обладающие способностью принимать свою первоначальную геометрическую форму при мартенситных переходах [1]. Это свойство материалов позволяет проектировать на их основе устройства, находящие широкое применение в различных областях науки и техники. На их основе созданы элементы аппаратуры, которые служат в системах автоматического пожаротушения, регулировки температуры, системах, контролирующих расход теплоносителей и т.д. Создание блока, содержащего элемент, изготовленный из материала с ЭПФ, сопряженный с кинематическим механизмом, позволяет создавать устройства, которые обладают большой величиной развиваемых усилий при требуемых перемещениях, и, в то же время, обладают простой компоновкой [2,3]. Особое положение в этой группе устройств занимают многократные приводы, действие которых основано на обратимых мартенситных переходах. Эти приводы представляют собой системы, состоящие из силового элемента, изготовленного из материала с ЭПФ и упругого контртела, представляющего собой, как правило, упругую пружину. В основе работы такого привода лежит тот факт, что изменение модуля сдвига силового элемента и контртела при мартенситном переходе будут различными. При прямом мартенситном переходе аустенит – мартенсит, который происходит при охлаждении в диапазоне температур (М_К˂ Т ˂ М_Н), контртело деформирует силовой элемент, а при обратном мартенситном переходе мартенсит - аустенит, который происходит при нагреве в области температур (А_Н ˂ Т ˂ А_К), вследствие наличия эффекта памяти формы, силовой элемент принимает свою первоначальную геометрическую форму. Здесь М_Н, М_К– температуры начала и конца перехода аустенит – мартенсит, А_Н, А_К – температуры начала и конца перехода мартенсит – аустенит, соответственно.

Проектирование такой системы привода направлено на расчет геометрических характеристик рабочих элементов и возвращаемой деформации силовым элементом, необходимых для работы конкретного механизма.

Несмотря на большой объем исследований, проведенных на сплавах, обладающих ЭПФ, остаются нерешенными вопросы расчета рабочих элементов на их основе. Это обусловлено тем, что поскольку сложность процессов, протекающих в устройствах, содержащих элемент из материала с ЭПФ, делает затруднительным переход от математической модели к реальному объекту [4,5].

Модель и основные уравнения

В данной работе предложен вариант модели, описывающей систему привода, состоящую из силового элемента, представляющего собой пружину из сплава с ЭПФ, а в качестве контртела используется упругая контрпружина [2]. Эти две пружины размещены на штоке и обе работают на сжатие.

Термоциклирование пружины с ЭПФ в интервале М_К ˂ Т ˂ А_К обеспечивает работу привода двунаправленного действия с поступательным движением штока. На рис. 1 представлена схема работы привода.

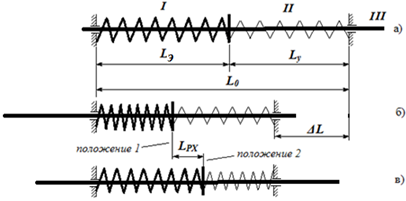
Рис.1 - І – пружина с ЭПФ;  ІІ – упругая контрпружина; III – шток: а) - привод в начальном состоянии ; б) в рабочем состоянии при температуре Т ≤ М_К , в);  А_К  ≤  Т (в)

Расчет системы направлен на определение взаимосвязи геометрических параметров рабочих элементов с их предварительной осадкой ∆L для обеспечения заданной величины рабочего хода L_PX исполнительного звена.

Первоначальная длина привода L₀ , согласно рис.1а определяется выражением:

  (1)

где L_S – длина пружины с ЭПФ и L_E – длина контрпружины, которые определяются с помощью следующих уравнений:

  (2)

 (3)

где   – шаг намотки и число витков  пружины с ЭПФ и упругой контрпружины, соответственно.

Для установки привода в рабочее положение ему необходимо при охлаждении в диапазоне температур прямого мартенситного перехода, определяемого условием М_К ˂ Т ˂ М_Н задать первоначальную осадку ∆L. В результате чего пружина с ЭПФ и упругая контрпружина получают соответствующие осадки , а шток привода занимает в крайнее левое положение (рис.1б положение 1). При этом для первоначальной осадки имеет место равенство:

  (4)

При нагреву рабочего элемента в диапазоне температур обратного мартенситного перехода А_Н ˂ Т ˂ А_К происходит проявление материалом ЭПФ. В этом случае осадка пружины с ЭПФ уменьшается, тем самым вызывая дальнейшее увеличение осадки и, как следствие, увеличение сил противодействия со стороны контрпружины, в результате чего система вновь переходит в состояние равновесия (рис.1в, положение 2).

В аустенитном состоянии, при температуре А_К ≤ Т осадки  пружины с ЭПФ и  контрпружины будут определяться выражениями:

  (5)

  (6)

где  – рабочий ход штока. В этом случае предварительная осадка ∆L привода будет определяться выражением:

  (7)

Поскольку суммарная осадка элементов привода всегда остается равной величине первоначальной осадки ∆L, то работу привода можно представить в виде диаграммы, изображенной на рис.2. Вследствие малости упругой деформации пружины с ЭПФ в мартенситном состоянии по сравнению с величиной деформации, вызванной проявлением ЭПФ, то ей можно пренебречь, причем для прямого превращения аустенит – мартенсит предполагается линейная зависимость между внешним усилием и деформацией [1].

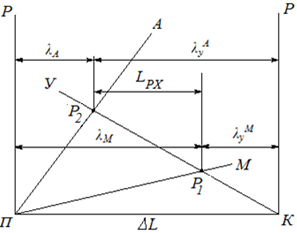
Рис.2 - Диаграмма работы привода системы: пружина из материала с ЭПФ - контрпружина, P – сила, DL – предварительная осадка

Диаграмма является комбинацией трех диаграмм деформирования: пружины c ЭПФ в мартенситном (луч „М”) и аустенитном (луч „А”) состояниях и упругой контрпружины (луч „У”).

Угол П диаграммы соответствует пружине с ЭПФ в исходном состоянии. Угол К диаграммы соответствует контрпружине в исходном состоянии. Расстояние между точками К и П соответствует величине предварительной осадки ∆L (рис.1б) элементов привода. Например, в точке П деформация пружины с ЭПФ отсутствует и вся предварительная деформация принадлежит  контрпружине. При движении от точки  П  в сторону точки К появляется деформация пружины с ЭПФ, которая увеличивается, а деформация контрпружины уменьшается. В точке К всю предварительную деформацию принимает на себя пружина с ЭПФ.

На диаграмме отмечены две характерные точки (Р_{1 ,} Р₂). Точка пересечения лучей „У ” и „М” соответствует  равновесному состоянию привода с внутренним усилием Р₁ при Т ≤ М_К (рис.1б). В свою очередь, точка пересечения лучей „У” и „А” соответствует равновесному состоянию привода с внутренним усилием Р₂  при  А_К ≤ Т (рис.1в). В этом случае расстояние между точками Р₁ и Р₂ по оси абсцисс будет соответствовать величине рабочего хода  L_РХ  исполнительного звена.

Из диаграммы (рис.2) видно, что при Т ≤ М_К в любом случае имеет место равенство:

  (8)

При этом, из условия равновесия элементов привода в точке Р₁ следует:   (9)

где C_У и С_М – характеристики упругой контрпружины и пружины с ЭПФ при Т ≤ М_К, соответственно.

Учитывая это, для упругой деформации контрпружины получим следующее выражение:

   (10)

Из условия равновесия привода в точке Р₂ следует следующее соотношение:    (11)

где  С_А  – характеристика пружины с ЭПФ при А_К ≤  Т. Тогда для деформации пружины с ЭПФ в аустенитном состоянии получим следующее выражение:

  (12)

Используя выражения (10 – 12) окончательно, для осадки  получим следующее уравнение:

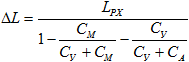   (13)

где характеристики контрпружины (С_у), пружины с ЭПФ в мартенситном  C_М  и аустенитном С_А  состояниях определяются следующими выражениями:

  (14)

   (15)

  (16)

где G_У , G_М , G_А – модули сдвига материала контрпружины в мартенситной (М) и  аустенитной (А) фазах, соответственно; D_У , d_У , n_У – средний диаметр витка, диаметр проволоки и количество витков контрпружины, соответственно; D_Э , d_Э , n_Э – соответственно средний диаметр витка, диаметр проволоки и  количество витков пружины с ЭПФ.

Следует отметить, что характеристики пружины с ЭПФ в интервале температур обратного мартенситного превращения (А_{Н ÷} А_К)  находятся в области, ограниченной лучами „М” и „А” (например луч „А₁” на рис.3). С повышением температуры луч „А₁” будет приближаться к лучу „А”. В связи с этим появляются возможности управления не только величиной, но и температурой начала рабочего хода исполнительного звена.

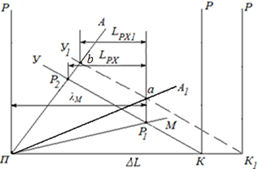
Рис.3 - Вариант управления величиной рабочего хода исполнительного звена за счет увеличения предварительной осадки привода. Осадка пружины с ЭПФ λ_М  = const

Например, увеличение предварительной осадки привода вызовет соответствующее перемещение луча „У” вправо (по схеме), который займет положение „У₁”, что, в свою очередь, вызовет соответствующее увеличение осадок пружин обоих типов.  Однако, если за счет конструктивных решений оставить осадку пружины с ЭПФ неизменной (λ_М  = const), то в интервале температур обратного мартенситного превращения изменение внутреннего усилия привода сначала пойдет по траектории Р₁ → а  и далее по лучу „У₁” до точки b. В результате рабочий ход исполнительного звена уменьшится и станет равным  L_РХ1 , а температура начала движения исполнительного звена повысится. Этот эффект дает возможность управлять температурой начала движения исполнительного звена.

Заключение

Таким образом, в работе получено уравнение, связывающее величину предварительной осадки ∆L  привода с характеристиками пружины с ЭПФ в мартенситном С_М и аустенитном C_А состояниях, с характеристикой C_У контрпружины  и величиной рабочего хода L_РХ  исполнительного звена.

Варьируя отдельно величинами предварительной осадки пружины с ЭПФ или контрпружины, можно управлять не только величиной рабочего хода, но и температурой начала движения исполнительного звена. Этот эффект используется в терморегулирующих устройствах [2, 3].

Представленный в работе метод расчета может быть использован для проектирования силовых установок с исполнительным элементом в форме винтовой цилиндрической пружины, изготовленной из материала, обладающего ЭПФ.

Список литературы / References

1. Лихачев В.А., Кузьмин С.Л., Каменцева З.П. Эффект памяти формы. Л.: Изд-во ЛГУ. (1987). 216с.
2. Вяххи И.Э. Движители на материалах с эффектом памяти формы // Инновации. – 1999, № 9-10, С. 97-99.
3. К. Ооцука, К. Симидзу, Ю. Судзуки и др. Сплавы с эффектом памяти формы Пер. с японского под ред. А.М. Глезера. М.: Металлургия, 1990. – 225 с.
4. Киквидзе О.Г. Уравнение состояния сплавов с эффектом памяти формы. // Проблемы машиностроения и надежности машин. – 1996, №2, С.51-55.
5. МовчанA. Аналитическое решение задач о прямом и обратном превращении для сплавов с памятью формы // Прикладная механика и техническая физика. – 1996. №4, С. 136-144.

Список литературы на английском языке / References in English

1. Likhachev V.A., Kuz’min S.L., Kamenzeva Z.P. Effect pamyati formi.[The shape memory effect] : Izd-vo LGU. [L.: Publishen house SPbSU](1987). 216с. [in Russian]
2. Vyakhkhi I.E. Dvizheteli na materialakh s effectom pamyati formi [Actuators on materials with shape  memory] // Innovatsii [Innovations]. – 1999, № 9-10, С. 97-99. [in Russian]
3. К. Ootsuka, К. Simizdu, Yu. Sudzuki I dr. Splavi s effectom pamyati formi Per. S yaponskogo pod red. A.M. Glesera. [Alloys with shape memory Translation from Japanese ed. A.M. Gleser] М.: Metallurgiya [M.:Metallurgy] – 225 с. [in Russian]
4. Kikvidze О.G. Uravnenie sostoyaniya splavov s effectom pamyati formi [The equation of state of alloys with shape memory effect]. // Problemi mashinostroeniya I nadezhnosti mashin.[The problems of mashine engineering and reliabity of mashins] – 1996, №2, С.51-55. [in Russian]
5. Movchan A. Analiticheskoe reshenie zadach o pryamom I obratnom prevracshenii dlya splavov s pamyat’yu formi [The analytical solution of problem on the direct and inverse transformation for alloys with shape memory] // Prikladnaya mekhanika I tekhnicheskaya fizika [Applied Mechanics and Technical Physics]. – 1996. №4, С. 136-144. [in Russian]