МОДЕЛИРОВАНИЕ ВЛИЯНИЯ ТРЕЩИНОВАТОСТИ И ПОРИСТОСТИ ГОРНЫХ ПОРОД НА СЕЙСМИЧЕСКИЙ СИГНАЛ

Ислямова А.А.

ORCID: 0000-0002-1790-1732, Ассистент кафедры геофизики, Национальный исследовательский, Томский политехнический университет

МОДЕЛИРОВАНИЕ ВЛИЯНИЯ ТРЕЩИНОВАТОСТИ И ПОРИСТОСТИ ГОРНЫХ ПОРОД НА СЕЙСМИЧЕСКИЙ СИГНАЛ

Аннотация

В работе рассмотрены сейсмические волны в трещиноватой или пористой среде, характерной для коллекторов углеводородов. Выявление признаков прохождения сейсмической волны через трещиноватые (пористые) зоны позволяет более эффективно прогнозировать свойства нефтегазовых месторождений. Созданы сейсмогеологические модели, описывающие слоистые, трещиноватые и пористые зоны с различной геометрией. Методом математического моделирования изучены спектральные характеристики сейсмических волн, прошедших через составленные модели. Результаты сравниваются с опубликованными данными других авторов, в том числе с результатами лабораторного моделирования. Получены генерализованные качественные и количественные характеристики, которые могут служить для обработки и интерпретации полевых данных.

Ключевые слова: сейсморазведка, трещиноватость, пористость, математическое моделирование, спектр Фурье.

Islyamova A.A.

ORCID: 0000-0002-1790-1732, Assistant of the Geophysics Department, National Research Tomsk Polytechnic University

MODELING OF SEISMIC SIGNAL IN FRACTURED AND POROUS ROCKS

Abstract

The paper deals with field of seismic waves in fractured or porous media, characteristic of hydrocarbon reservoirs. The determination of seismic wave propagation through fractured (porous) zone allows to predict properties of oil and gas fields more efficiently. Seismic models describing layered, fractured and porous zones with different geometry were created. Spectral characteristics of seismic waves passing through the created models were studied by mathematical modeling. The results were compared with published data of other authors, including the results of laboratory experiments. The obtained quantitative and qualitative characteristics that can be used for processing and interpretation of field data.

Keywords: seismic survey, fractured medium, porous medium, mathematical modeling, Fourier spectrum.

Введение

При разработке месторождений нефти и газа знание фильтрационно-емкостных свойств терригенного коллектора позволяет решать множество задач. В условиях осадочного чехла ключевую роль при этом играет пористость песчаников, вмещающих углеводороды. При освоении залежей нефти с карбонатными коллекторами особую роль играет также трещиноватость, т.к. неравномерность распределения трещин в продуктивной толще оказывает решающее влияние на фильтрационно-емкостные свойства коллекторов, поскольку в таких условиях дебиты добывающих скважин во многом определяются не структурным фактором, а трещиноватостью коллекторов. В предлагаемой работе некоторые аспекты влияния обоих факторов – и пористости, и трещиноватости  - на сейсмическое поле будут изучены с помощью конечно-разностного моделирования.

Метод конечно-разностного  моделирования

Моделирование процессов распространения сейсмических волн в образцах применяется довольно широко. В физических экспериментах в основном оцениваются скорости продольной и поперечных волн, реже амплитудные и частотные характеристики. Лабораторные модели пористой среды создаются на базе образцов горных пород или схожих синтетических материалов, причем необходимо учитывать требования подобия реальным геологическим ситуациям. Кроме того, присутствуют сложности с изменением свойств минерального скелета, флюида и структуры образцов, что является тривиальной задачей при применении численного моделирования. На этапе разработки математического алгоритма требуется сравнение результатов расчета с имеющимися результатами физических экспериментов для проверки его корректности.

В данной работе исследуется влияние трещиноватости и пористости горных пород на спектральные характеристики сейсмического сигнала, проходящего через данные зоны. Используется конечно-разностный метод HEMP[1], усовершенствованный в [2], с последующим сравнением с данными физических экспериментов. Выявленные закономерности служат целям выявления областей возможных коллекторов на реальных сейсмических разрезах.

При построении конечно-разностного алгоритма использована полная система уравнений механики сплошных сред с определяющими соотношениями для упруго-хрупкой модели [2]. В этой модели каждая трещина имеет два берега и описывается специальными граничными условиями.

Для тестирования алгоритма расчета волнового поля в случае среды с ансамблем пор была сгенерирована модель, эквивалентная пористому алюминию (спеченный Al‑6061), для которого имеются количественные данные физического моделирования [3]. В случае расчетов для среды с трещинами сравнение проводилось с лабораторным экспериментом Грегори[4].

Влияние трещиноватости на сейсмическое поле

Термином "трещиноватость" обычно характеризуют совокупность открытых макро- и микротрещин в заданном объеме горной породы. Значительная густота раскрытых трещин приводит к существенному затуханию сейсмических волн и возникновению рассеянных волн на совокупности трещин. Направленная трещиноватость приводит к появлению анизотропии механических свойств горных пород, что говорит о зависимости скорости распространения сейсмических волн от направления их распространения (эффективная анизотропия в данной работе не рассматривается).

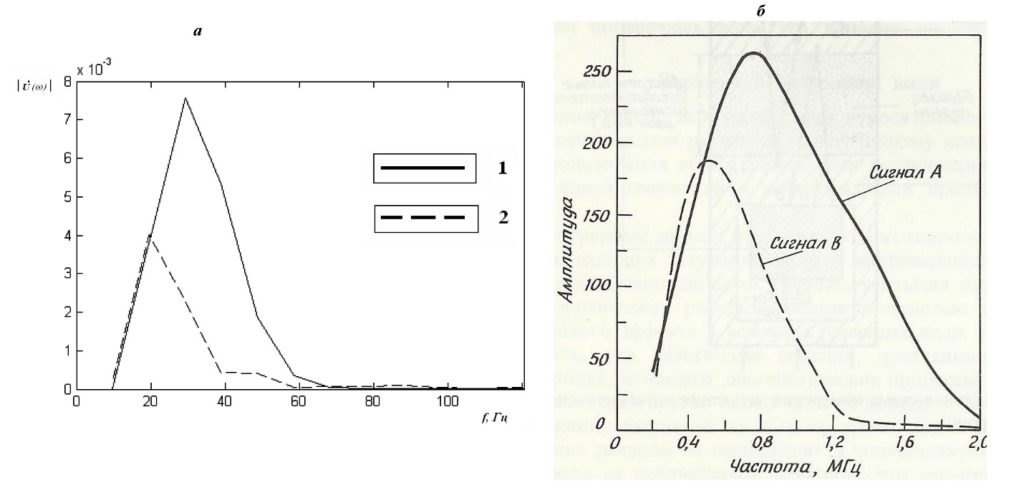
На неоднородностях (на трещиноватости) формируется поле рассеянных волн, и, хотя именно они могут служить наиболее информативным индикатором открытой трещиноватости, но относительная интенсивность рассеянных волн низка.  Однако динамические характеристики волнового поля за счет дифракции и потери энергии в трещиноватой области меняются. В работе [5] было показано количественно и качественно, что поглощение упругой энергии на отдельных трещинах приводит к изменению спектра прошедшего сигнала. Такое же изменение спектра обнаружено в описании лабораторного эксперимента Грегори [4]. Ниже на рис.1 приводится рис. 8 из работы [5]. На нем представлены амплитудные спектры Фурье для сигнала, прошедшего через трещиноватый образец.  Как хорошо видно, изменения спектра сигнала для расчетного волнового поля (рис. 1, а) и для сигнала, зарегистрированного в эксперименте (рис. 1, б)  находятся в хорошем соответствии.

Рис. 1 - Приводится из работы [5], а – численное моделирование, б – лабораторный эксперимент

Подытоживая рассмотрение трещиноватых коллекторов, нужно особо выделить тот факт, что в амплитудном спектре после прохождения трещиноватой области вырезается часть частот.

Влияние пористости на сейсмическое поле

Известно, что на свойства сейсмических волн влияют любые неоднородности среды, в том числе пустоты осадочных горных пород пористой структуры. Степень влияния зависит от соотношения «длина волны/характерный размер поры», от величины пористости, от топологии пористого пространства.

Для пористых сред, так же, как и для трещиноватых, создано много способов лабораторного моделирования. Один из них, с использованием спеченного алюминия Al-6061, приведен в работе [3]. На рис 2 приведен рис. 1 из работы [3], на нем изображена мезоструктура лабораторных образцов. Для пористости 9% (рис. 2, а) измеренная скорость распространения продольной волны составила V_p(9%)=5125 м/с, а для пористости  17% (рис. 2, б)  V_p(17%)=4120 м/с.

В ходе численного моделирования скорости распространения продольной волны составили соответственно 5123 м/с и 4074 м/с.

Рис. 2 - Мезоструктура пористого алюминия (Fig 1 из [3])

 

Таким образом, при численном моделировании значения скоростей в пористом алюминии отличались от скоростей из эксперимента при пористости 9% всего на 0,04 %; а при пористости 17 % отличие составило 1,1 %. Это позволяет оценивать использованный метод как достаточно адекватно описывающий сейсмические (упругие) волновые поля в пористых средах.

Нам интересно далее сравнить амплитудные спектры Фурье, вычисленные для сейсмической волны до падения на пористый слой, и после прохождения такого слоя. Ранее, в работе [6], нами была смоделирована дифракция упругих волн на пористом слое, но спектральные характеристики там не рассматривались. Ниже на рис. 3 показаны амплитудные спектры Фурье для падающей волны (рис. 3, а) и для волны преломленной (рис. 3, б).

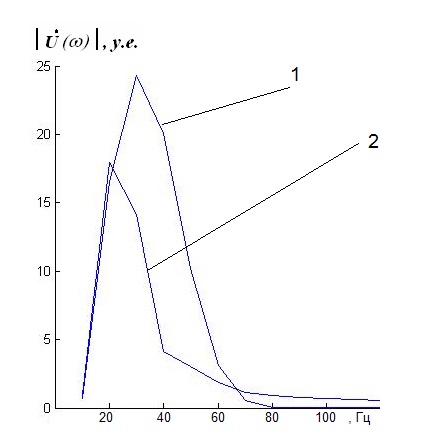
Рис. 3 - Спектры падающей (1) и преломленной (2) волн

 

Хорошо видно, что спектры волн, прошедших через трещиноватую среду (рис. 1, а) и через пористую среду (рис. 3, 2), в значительной степени сходным образом лишаются не только высоких, но и несущих частот.

Сопоставление частот и спектров   

Сейсморазведка проводится в диапазоне частот, редко превышающим 100 Гц (длина волны составляет первые десятки метров). При обработке данных сейсморазведки используются, кроме всего прочего, результаты исследований в скважинах - данные акустического каротажа. Эти данные получаются на частотах звукового (0,5-15 кГц) и ультразвукового (20-50 кГц, 0,3-2,0 МГц) диапазонов (длина волны в последнем случае – первые миллиметры). По результатам измерений строят геоакустические модели разрезов скважин для интерпретации данных сейсморазведки, проводят оценку пористости продуктивных пластов, определяют упругие модули горных пород и т.д.

Таким образом, частоты и результаты при физическом моделировании сопоставимы с частотами и данными акустического каротажа, а последний служит для анализа результатов сейсморазведочных работ. С другой стороны, упругие свойства керна и породы в скважине определяются почти исключительно по скоростям распространения продольной и поперечной волн. Численное моделирование позволяет, меняя свойства скелета и замещая один флюид другим, строить модели, наиболее близко отвечающие как данным каротажа, так и сейсморазведки.

Это свойство спектров возможно применять при обработке реальных временных разрезов.

Применение преобразований Прони и Фурье при обработке временных разрезов

Различия в спектральной характеристике исходной волны и волны, прошедшей через трещиноватые или пористые области, очевидны. Поэтому следующим шагом работы стало определение зон ослабления и изменения спектров на реальных сейсмограммах. Для этого при дальнейшей обработке реальных временных разрезов использовались преобразования Прони [7] и Фурье в скользящем окне.

На рис. 4 показан фрагмент временного разреза по одному из профилей на месторождении «Д» Западной Сибири. Фрагмент слева (рис. 4, а) соответствует исходному временному разрезу (формат SEG-Y после стандартного графа обработки), а фрагмент справа (рис. 4, б) – тот же фрагмент после обработки в спектральной области с последующим восстановлением во временную. Алгоритм обработки в данной работе не приводится, а суть его – в полосовой режекторной фильтрации.

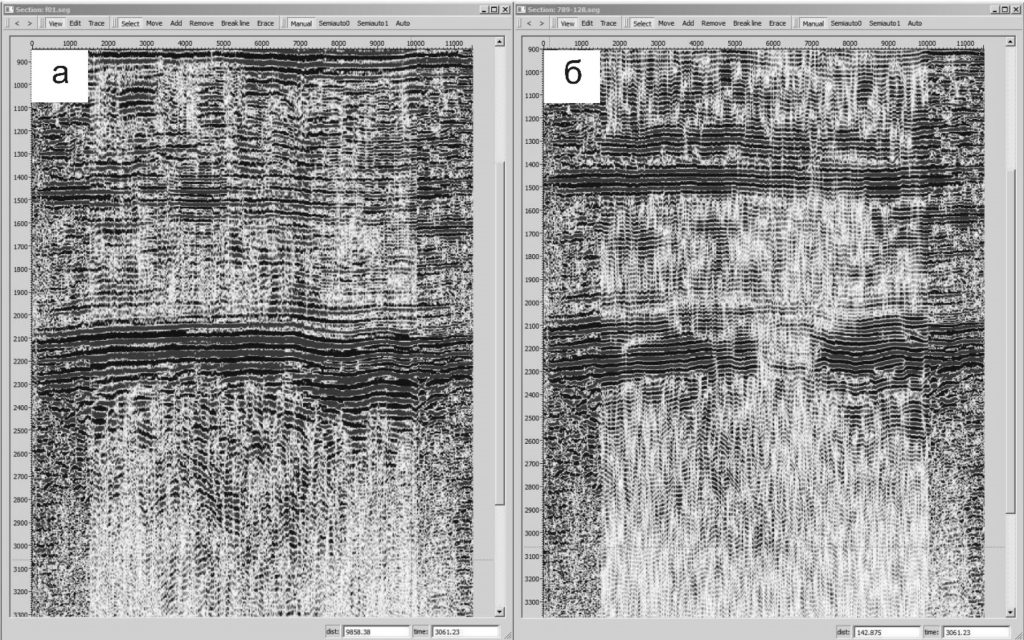
Рис. 4 - Cейсмический разрез 950430 по Двуреченской площади до (а) и после (б) применения оконной фильтрации

 

Благодаря примененному нами графу обработки разреза, зоны неоднородностей (возможно, повышенной трещиноватости/пористости и/или флюидонасыщенности) должны выделяться на разрезе меньшими амплитудами волны, по сравнению с окружающими трассами. Такой эффект мы наблюдаем в средней части профиля 950430 на временах 2100-2300 мс, где среди четких фаз юрских горизонтально-слоистых отложений осадочного чехла появляется лакуна с нарушением чередования и прослеживания фаз, низкими амплитудами волн. Необходимо отметить, что найденная зона (лакуна) соответствует реальному продуктивному интервалу.

Заключение

В работе с единых позиций рассмотрены трещиноватость и пористость геологических сред с точки зрения проявления этих свойств в сейсмическом поле. Для трещиноватой среды рассчитаны спектры Фурье, которые сравниваются с данными лабораторного моделирования. В случае пористого слоя по результатам численного моделирования были оценены средние скорости продольной волны в слое, значения скоростей сопоставлены с данными физического моделирования. И в том, и в другом случае в спектрах сигналов при прохождении через среду, осложненную порами(трещинами), устойчиво уменьшаются значения частотном диапазоне около несущей частоты и выше. Это позволяет создать и применить оконную фильтрацию (как Фурье, так и Прони) для выделения зон возможных коллекторов при поисках залежей углеводородов.

 

Список литературы / References

1. Wilkins, M.L. Computer Simulation of Dynamic Phenomena / M.L. Wilkins, – Springer-Verlag, 1999, ISBN: 978-3-642-08315-0.
2. Nemirovich-Danchenko M. M. A model for the brittle hypoelastic medium: application to computation of deformations and failure in rock //Physical Mesomechanics. – 1998. – V. 2. – P. 101-108.
3. Bonnan S., Hereil P-L., Collombet F. Experimental characterization of quasi static and shock wave behavior of porous aluminum // Journal of applied physics. – 1998. – V. 83. – No. 11. – P. 5741-5749.
4. Payton C. E. et al. (ed.). Seismic stratigraphy: applications to hydrocarbon exploration. – Tulsa, OK : American Association of Petroleum Geologists, 1977. – V. 26. – P. 1-516.
5. Немирович-Данченко М. М. Возможности обнаружения множественной трещиноватости сплошной среды на основе оценки спектральной плотности энергии отраженного сигнала // Физическая мезомеханика. – 2013. – Т. 16. – №. 1. - С. 105-110.
6. Немирович-Данченко М.М., Шатская А.А. Численное моделирование распространения сейсмических волн в среде,содержащей одиночную пору или пористый слой // Физическая мезомеханика. – 2015. – Т. 18. – № 3. - С. 101-104.
7. Marple Jr S. L., Carey W. M. Digital spectral analysis with applications //The Journal of the Acoustical Society of America. – 1989. – V. 86. – №. 5. – P. 2043-2043.

Список литературы на английском языке / References in English

1. Wilkins, M.L. Computer Simulation of Dynamic Phenomena / M.L. Wilkins, – Springer-Verlag, 1999, ISBN: 978-3-642-08315-0.
2. Nemirovich-Danchenko M. M. A model for the brittle hypoelastic medium: application to computation of deformations and failure in rock //Physical Mesomechanics. – 1998. – V. 2. – P. 101-108.
3. Bonnan S., Hereil P-L., Collombet F. Experimental characterization of quasi static and shock wave behavior of porous aluminum // Journal of applied physics. – 1998. – V. 83. – No. 11. – P. 5741-5749.
4. Payton C. E. et al. (ed.). Seismic stratigraphy: applications to hydrocarbon exploration. – Tulsa, OK : American Association of Petroleum Geologists, 1977. – V. 26. – P. 1-516.
5. Nemirovich-Danchenko M.M. Vozmozhnosti obnaruzhenija mnozhestvennoj treshhinovatosti sploshnoj sredy na osnove ocenki spektral'noj plotnosti jenergii otrazhennogo signala [Possibilities of detection of continuous media multiple fractures based on the evaluation of the spectral power density of the reflected signal] // Fizicheskaja mezomehanika [Physical mesomechanics] - 2013. - V. 16. - № 1. - P. 105-110.
6. Nemirovich-Danchenko M.M., Shatskaya A.A. Chislennoe modelirovanie rasprostranenija sejsmicheskih voln v srede, soderzhashhej odinochnuju poru ili poristyj sloj [Numerical modeling of seismic wave propagation in a medium containing a single pore or porous layer] // Fizicheskaja mezomehanika [Physical mesomechanics] - 2015. - V. 18. - № 3. - P. 101-104.
7. Marple Jr S. L., Carey W. M. Digital spectral analysis with applications //The Journal of the Acoustical Society of America. – 1989. – V. 86. – №. 5. – P. 2043-2043.