АВТОМАТИЗАЦИЯ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
Батурина Н.Ю.
Кандидат технических наук, Донской государственный технический университет (Ростов-на-Дону)
АВТОМАТИЗАЦИЯ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
Аннотация
Разработано приложение на базе VBA для Excel и Access, предназначенное для автоматизации планирования многофакторных экспериментов. Приложение содержит блок планирования на основе ортогонального центрального композиционного плана; блок проведения эксперимента, включающий импорт значений показателей качества в точках плана; блок регрессионного и дисперсионного анализа: уравнение регрессии находится в виде полинома второго порядка, его значимость оценивается по критерию Фишера; блок прогнозирования поведения объекта при изменении исходных данных.
Ключевые слова: ортогональный центральный композиционный план второго порядка, автоматизация планирования эксперимента.
Baturina N.Yu.
PhD in Engineering, Donskoy state technical university (Rostov-on-Don)
AUTOMATION OF PLANNING OF EKSPERIMEN
Abstract
Developed an application based on VBA for Excel and Access, equipm-chennoe planning multifactor experiments. The app includes a scheduling unit based on an orthogonal central com-point plan; block of the experiment, including the import of quality indicators values at the points of the plan; block regression and dis-persion analysis - regression equation is in the form of a WTO-order polynomial, its significance is assessed by the Fisher test; block pro-prediction behavior of the object when you change the source data.
Keywords: orthogonal central composite plan of the second order, automation of planning of an experiment.
Для повышения эффективности исследований, связанных с проведением натурных или модельных экспериментов необходимо выполнение следующих требований:
- обеспечение получения достоверных результатов экспериментов при наименьших затратах;
- организация хранения исходных данных и результатов экспериментов, удобство их извлечения для анализа и дальнейшего использования;
- возможность прогнозирования поведения объекта при изменении входных параметров и их оптимизация по критериям качества.
Целью проводимой работы являлась разработка приложения, обеспечивающего выполнение перечисленных требований.
Автоматизация вычислительных операций, обмен данными между пакетами MS Office Access и MS Office Excel реализованы с помощью VBA. Для планирования экспериментов в данной работе применялся ортогональный центральный композиционный план второго порядка (ОЦКП) [1]. При необходимости приложение может быть дополнено другими схемами планирования. Значимость уравнения регрессии оценивалась по критерию Фишера [2]. Нужно заметить, что несмотря на большое количество литературы, посвященной вопросам планирования экспериментов, проблема автоматизации хранения, передачи и обработки данных и результатов экспериментов раскрыта недостаточно. Данная работа является развитием ранее опубликованной статьи [3].
Структурно разработанное приложение состоит из следующих блоков: планирование эксперимента, проведение эксперимента, регрессионный и дисперсионный анализ, прогнозирование, критерий Фишера. Блоки работают независимо друг от друга. Каждый блок представлен отдельной формой, вызываемой из начальной формы после выбора количества факторов .
Расчетная часть приложения реализована c помощью макросов. Для каждого и каждого критерия используется отдельный лист типа CALC_y книги Excel. Эти листы расчетов являются «защищенными», и не могут быть удалены пользователем приложения из книги.
Для каждого выбранного количества факторов приложение создает в книге Excel и БД Access определенные типы таблиц. Таблицы типа GREXP с ключевым полем ID содержат диапазоны изменения факторов. Таблицы типа XPLN и YPLN c ключевыми полями number содержат координаты точек плана для проведения натурных или модельных экспериментов и значения критериев в этих точках. Соответствующие листы в книге Excel могут автоматически добавляться и удаляться. Таблицы типа COEF с ключевым полем ID содержат значения коэффициентов уравнения регрессии и признак значимости уравнения, рассчитанный на основании критерия Фишера. Таблицы типа RESULT содержат результаты вычислительных экспериментов, полученные с помощью уравнения регрессии.
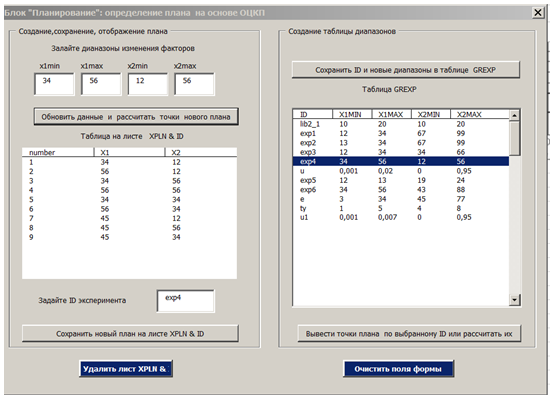
На рис. 1 представлена форма блока «Планирование эксперимента».
В блоке «Планирование эксперимента» рассчитываются точки нового плана по вводимым в текстовые поля диапазонам изменения факторов ![]() , или выводится план, созданный ранее в базе данных. Количество точек плана N при ортогональном центральном композиционном планировании определяется в зависимости от количества факторов n по формуле
, или выводится план, созданный ранее в базе данных. Количество точек плана N при ортогональном центральном композиционном планировании определяется в зависимости от количества факторов n по формуле ![]() , среди которых 2n точек - ядро планирования, 2n точек - звездные точки и одна центральная.
, среди которых 2n точек - ядро планирования, 2n точек - звездные точки и одна центральная.
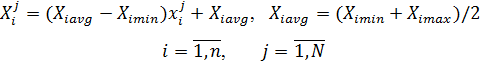
где ![]() значение кодированного фактора
значение кодированного фактора ![]() в j-ой точке плана.
в j-ой точке плана.
В результате работы блока в базе данных Access и в книге Excel создаются таблица диапазонов (групп экспериментов) GREXP и таблица плана XPLN, связанные отношением ![]() по ключевому полю ID, содержащему код группы экспериментов.
по ключевому полю ID, содержащему код группы экспериментов.
Рис. 1 - Блок «Планирование эксперимента» при двух факторах
В блоке «Проведение эксперимента» по выбранному из таблицы GREXP варианту выводятся точки плана. Значения критериев ![]() - количество критериев (показателей качества), найденные в точках плана по результатам натурного или модельного эксперимента, могут импортироваться из файла или вводиться в текстовые поля формы. Данные эксперимента с выбранным ID сохраняются в таблице YPLN. Таблицы XPLN и YPLN связаны отношением
- количество критериев (показателей качества), найденные в точках плана по результатам натурного или модельного эксперимента, могут импортироваться из файла или вводиться в текстовые поля формы. Данные эксперимента с выбранным ID сохраняются в таблице YPLN. Таблицы XPLN и YPLN связаны отношением ![]() по ключевому полю number.
по ключевому полю number.
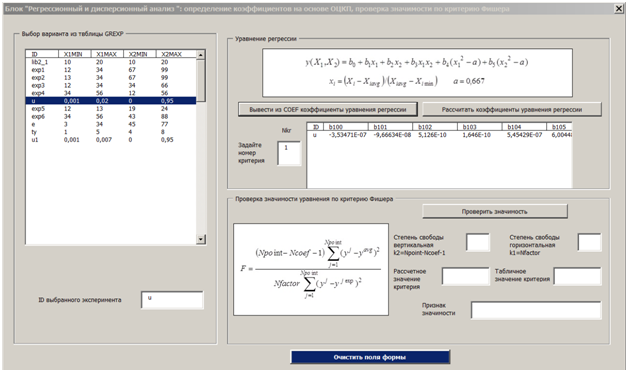
В блоке «Регрессионный и дисперсионный анализ» для выбранного варианта из таблицы GREXP выполняется расчет коэффициентов функции отклика. Функция отклика определяется в виде полинома второго порядка относительно кодированных переменных:
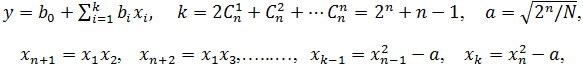
где ![]() – кодированные переменные; k - количество коэффициентов уравнения.
– кодированные переменные; k - количество коэффициентов уравнения.
Коэффициенты функции отклика вычисляются по формулам:
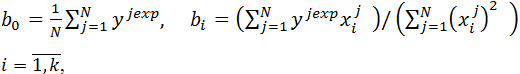
где ![]() значение фактора
значение фактора ![]() ,
, ![]() - экспериментальное значение критерия в j-ой точке плана.
- экспериментальное значение критерия в j-ой точке плана.
В результате работы блока «Регрессионный и дисперсионный анализ» в базе данных и в книге Excel создается таблица коэффициентов COEF. Эта таблица связана отношением ![]() с таблицей GREXP.
с таблицей GREXP.
Рис. 2 -Блок «Регрессионный и дисперсионный анализ» при двух факторах
Значимость уравнения регрессии в целом оценивалась по критерию Фишера. Эмпирическое значение критерия Фишера вычисляется как отношение факторной дисперсии к остаточной дисперсии, приходящихся на одну степень свободы:
![]()
где ![]() - значения критерия в j-ой точке плана, полученные в результате регрессионного анализа с помощью ОЦКП;
- значения критерия в j-ой точке плана, полученные в результате регрессионного анализа с помощью ОЦКП; ![]() - среднее значение критерия по экспериментальным данным
- среднее значение критерия по экспериментальным данным ![]() .
.
Если эмпирическое значение критерия Фишера оказывается больше табличного ![]() при заданном уровне значимости, то полученное уравнение регрессии принимается как значимое. В таблице COEF заполняется поле «значимости» equatVal, в котором фиксируется для каждого уравнения его значимость или незначимость.
при заданном уровне значимости, то полученное уравнение регрессии принимается как значимое. В таблице COEF заполняется поле «значимости» equatVal, в котором фиксируется для каждого уравнения его значимость или незначимость.
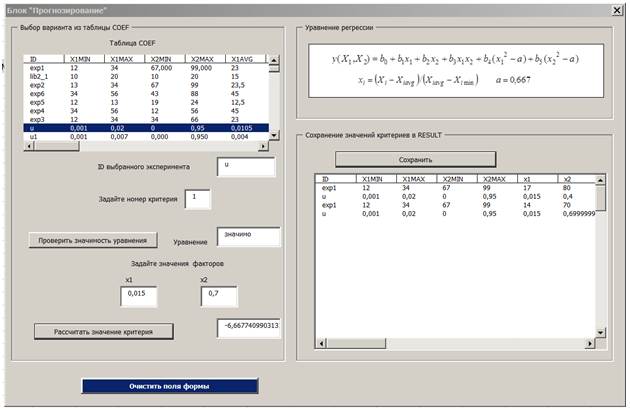
Рис. 3 -Блок «Прогнозирование» при двух факторах
В блоке «Прогнозирование» (рис. 3), задавшись произвольными значениями факторов ![]() из выбранных диапазонов таблицы GREXP, без проведения дорогостоящего натурного или модельного эксперимента вычисляются значения выбранного критерия на основании данных таблицы COEF по формулам:
из выбранных диапазонов таблицы GREXP, без проведения дорогостоящего натурного или модельного эксперимента вычисляются значения выбранного критерия на основании данных таблицы COEF по формулам:
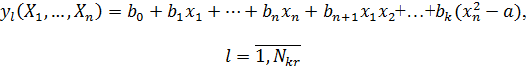
где ![]()
- кодированные переменные, выраженные через натуральные ![]()
Результаты расчетов записываются в таблицу RESULT, связанную отношением ![]() с таблицей GREXP.
с таблицей GREXP.
В блоке «Критерий Фишера» оценивается значимость полученного уравнения регрессии по дополнительным экспериментальным точкам, которые изначально не входили в точки плана.
Разработанное приложение позволяет:
- создавать новый объект исследования в базе данных или выбирать для исследования созданный ранее;
- автоматизировать обработку результатов многофакторных экспериментов, сохранять результаты регрессионного и дисперсионного анализа в базе;
- прогнозировать поведение исследуемого объекта при измененных значениях входных параметров и вырабатывать рекомендации по оптимизации их значений.
Приложение использовалось для планирования экспериментов по имитационному моделированию в среде Arena [3], виброизмерительных экспериментов при оценке состояний дорожных покрытий [4].
Список литературы / References
- Налимов В. Н. Статистические методы планирования экстремальных экспериментов/ В. Н. Налимов, Н. А. Чернова. - М.: Наука, 1965. -340 с.
- Дубров А. М. Многомерные статистические методы: Учебник / А. М. Дубров, В. С. Мхитарян , Л. И. Трошин. - М.: Финансы и статистика, 2003. - 352 c.
- Батурина Н.Ю. Разработка информационной системы для проведения оптимальных экспериментов [Электронный ресурс] // Евразийский союз ученых (ЕСУ). Ежемес. науч. журн. - - № 5 (26)/2016, ч. 2. - С. 18-20. - URL: http://euroasia-science.ru/wp-content/uploads/2016/08/euroasia_26_p2_5-144.pdf. (дата обращения: 20.10.2016).
- Uglova E. V. Integrated approach to studying characteristics of dynamic deformation on flexible pavement surface using nondestructive testing / E. V. Uglova, A. N. Tiraturyan, A. A. Liapin // PNRPU Mechanics Bulletin. - - № 2. - Р. 111-130.
Список литературы на английском языке / References in English
- Nalimov V. N. Statisticheskie metody planirovanija jekstremal'nyh jeksperimentov [Statistical methods of planning extreme experiments] / V. N. Nalimov, N. A. Chernova. - M.: Nauka, 1965. - 340 p. [ in Russian]
- Dubrov A. M. Mnogomernye statisticheskie metody: Uchebnik [Multivariate statistical methods: a Textbook] / A. M. Dubrov, V. S. Mhitarjan , L. I. Troshin. - M.: Finansy i statistika, 2003. - 352 p. [ in Russian]
- Baturina N.Ju. Razrabotka informacionnoj sistemy dlja provedenija optimal'nyh jeksperimentov [Development of the informative system for realization of optimal experiments ] [Jelektronnyj resurs] // Evrazijskij sojuz uchenyh (ESU). Ezhemes. nauch. zhurn. - 2016. - № 5 (26)/2016, ch. 2. - P. 18-20. - URL: http://euroasia-science.ru/wp-content/uploads/2016/08/euroasia_26_p2_5-144.pdf. (data obrashhenija: 20.10.2016) [ in Russian]
- Uglova E. V. Integrated approach to studying characteristics of dynamic deformation on flexible pavement surface using nondestructive testing / E. V. Uglova, A. N. Tiraturyan, A. A. Liapin // PNRPU Mechanics Bulletin. - - № 2. - Р. 111-130.