МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МНОГОФАЗНОЙ ЗАТОПЛЕННОЙ СТРУИ

Кильдибаева С.Р.

Аспирант, Стерлитамакский филиал Башкирского государственного университета

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ МНОГОФАЗНОЙ ЗАТОПЛЕННОЙ СТРУИ

Аннотация

В статье рассматриваются математические модели многофазной затопленной струи. Струя состоит из капель нефти и пузырьков газа. В работе проведен расчеты теплофизических параметров затопленной струи, получены графики зависимости температуры и скорости от вертикальной координаты. Особенное внимание в исследовании струи уделено процессу охлаждения струи из-за «захвата» окружающей воды. С течением времени температура струи охлаждается до температуры гидратообразования. С ростом вертикальной координаты увеличение скорости струи замедляется, что вызвано увеличением массы струи.

Ключевые слова: затопленная струя, гидрат, миграция углеводородов

Kildibaeva S.R.

Post graduate student, Sterlitamak branch of Bashkir State University

MATHEMATICAL MODEL MULTIPHASE SUBMERGED JET

 Abstract

In article are considered mathematical model of multiphase submerged jets. Multiphase jet consists of oil and gas bubbles. In this paper we calculated the thermal parameters of the submerged jet, obtained plots of the temperature and velocity of the vertical coordinate. Particular attention is paid to the study of the jet spray cooling process because of the "capture" of the surrounding water. With the passage of time, the temperature of the jet is cooled to a temperature of hydrate formation. With the growth of the vertical coordinate increase in jet velocity slows down, which is caused by the increase in mass of the jet.

Keywords: submerged jet, hydrate, migration of hydrocarbons

Изучение затопленных струй актуально в связи с увеличением объемов глубоководной добычи углеводородов и проблемой охраны прибрежной и шельфовой зоны морей от загрязнения [6]. Возможные масштабы загрязнения водоемов зависят от подводных течений водоемов, от интенсивности выбросов и их теплофизических характеристик, глубины залегания трубопроводов, размеров и характера разрывов [2]. Моделирование струи используется для создания математических моделей устройств, предназначенных для сбора нефтепродуктов при их разливе [3,4].

При истечении струи в жидкость изменению подвергаются следующие параметры: скорость течения, температура, концентрация примеси, при этом возникают вихри, движущиеся вдоль и поперек потока, и между соседними струями происходит обмен конечными массами. На границе двух струй формируется область конечной толщины с непрерывным распределением скорости, температуры и концентрации примеси.

Рассмотрим следующую задачу. Пусть на дне океана из устья скважины вытекает смесь нефти и газа. Предположим, что известны объемные расходы, теплофизические параметры нефти, газа и окружающей воды. Требуется произвести расчет параметров многофазной струи.

Рассмотрим распределение температуры нефти и газа в струе. Предположим, что капли нефти, пузырьки газа и вода, вовлекаемая в струю, имеют одинаковые температуру, скорость и траекторию в каждом сечении струи. Ось z, направлена вертикально вверх. При расчетах используем методику, предложенную в [7].

Начальная площадь поперечного сечения струи: , где D=2B₀, B₀ – радиус скважины.

Скорость течения смеси определим как , здесь Q^o₀, Q^g₀ – начальные объемные расходы нефти и газа.

Удельный поток импульса на устье: M₀=Q₀V_o.

Сила плавучести на единицу массы представляется в виде: ,

где ρ_w – плотность окружающей воды, ρ – плотность истекающей смеси, g – ускорение свободного падения.

Удельный поток плавучести: F_o=g'_o·Q₀.

Расстояние, на котором удельный импульс силы плавучести превышает удельный импульс, приобретаемый струей вначале: .

Время для перемещения объема жидкости на расстояние z: .

Радиус струи на высоте z представляется в виде: .

Скорость подъема струи в сечении z: .

Объемный расход представим в следующем виде: Q=πwB².

Таким образом, можно определить температуру в любом сечении струи, считая, что температура в сечении струи одинаковая и зависит только от координаты z:

,

где T_w, T₀ – температуры окружающей воды и вытекающей жидкости, Q₀ – начальный объемный расход.

Далее представлены зависимости параметров струи от высоты z, полученные на основе численного решения. Для параметров расчета приняты следующие значения: B₀=1.7 м, T_w=4 °C, Q₀=1м³/с, α=0.149.

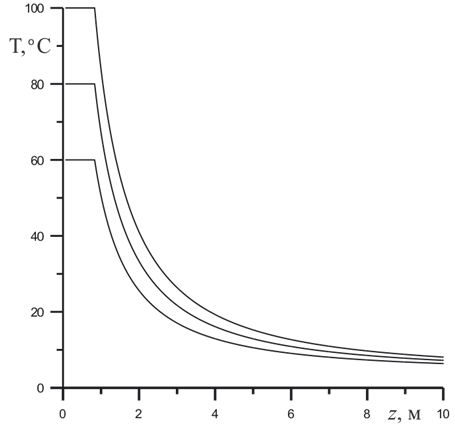
Рис.1 - Зависимость температуры струи от вертикальной координаты

На рис.1 представлена зависимость температуры струи от вертикальной координаты z для начального значения поступающих углеводородов T₀=100°C, T₀=80°C, T₀=60°C. Из графика видно, что на расстоянии z=10 м температура струи остывает до значения T_jet=8.0°C, T_jet=7.2°C, T_jet=6.4°C. При давлении 150 атм. равновесная температура гидратообразования составляет 21°C, что говорит о том, до того как температура в струе ниже данной, происходит процесс гидратообразования.

В работе рассмотрена модель затопленной струи, проведены расчеты теплофизических и кинематических параметров, получены графики зависимости температуры струи от вертикальной координаты. Вследствие «захвата» окружающей воды струей происходит охлаждение струи до температуры окружающей среды.

Работа выполнена при поддержке гранта СФ БГУ, договор № В14-6.

 

Литература

1. Абрамович Г.Н. Теория турбулентных струй. М.: ЭКОЛИТ, 2011.– 720 с.
2. Гильманов С.А., Шабаев Р.Б. Экспериментальное исследование струй положительной плавучести в воде // Современные проблемы физики и математики. – 2004. – Т. 2. – С. 44-48.
3. Кильдибаева С.Р. Моделирование купола-сепаратора при разливе нефти в шельфе // Фундаментальные исследования. – 2013. – № 10 (часть 5). С. 1045-1050.
4. Кильдибаева С.Р., Гималтдинов И.К. Математическая модель наполнения купола нефтью. // Математическое моделирование в естественных науках: материалы XXII Всероссийской школы-конференции молодых ученых и студентов (Пермь, Пермский национальный политехнический университет, 2-5 октября 2013г.), – Пермь, 2013. – С.79-80.
5. Маликов З.М., Стасенко А.Л. Асимптотика затопленной струи и процессы переноса в ней // Труды МФТИ. Аэрогидромеханика. – 2013. – Т. 5, № 2. – С. 59-68.
6. Мельников Н.Н., Калашник А.И. Шельфовые нефтегазовые разработки западного сектора российской Арктики: геодинамические риски и безопасность // Газовая промышленность. – 2011. – № 661. – С. 46-55.
7. Lee J.H.W., Chu V.H. Turbulent jets and plumes – a Lagrangian approach. Kluwer Academic Publishers, 2003. – 390 p.

References

1. Abramovich G.N. Teorija turbulentnyh struj. M.: JeKOLIT, 2011.– 720 s.
2. Gil'manov S.A., Shabaev R.B. Jeksperimental'noe issledovanie struj polozhitel'noj plavuchesti v vode // Sovremennye problemy fiziki i matematiki. – 2004. – T. 2. – S. 44-48.
3. Kil'dibaeva S.R. Modelirovanie kupola-separatora pri razlive nefti v shel'fe // Fundamental'nye issledovanija. – 2013. – № 10 (chast' 5). S. 1045-1050.
4. Kil'dibaeva S.R., Gimaltdinov I.K. Matematicheskaja model' napolnenija kupola neft'ju. // Matematicheskoe modelirovanie v estestvennyh naukah: materialy XXII Vserossijskoj shkoly-konferencii molodyh uchenyh i studentov (Perm', Permskij nacional'nyj politehnicheskij universitet, 2-5 oktjabrja 2013g.), – Perm', 2013. – S.79-80.
5. Malikov Z.M., Stasenko A.L. Asimptotika zatoplennoj strui i processy perenosa v nej // Trudy MFTI. Ajerogidromehanika. – 2013. – T. 5, № 2. – S. 59-68.
6. Mel'nikov N.N., Kalashnik A.I. Shel'fovye neftegazovye razrabotki zapadnogo sektora rossijskoj Arktiki: geodinamicheskie riski i bezopasnost' // Gazovaja promyshlennost'. – 2011. – № 661. – S. 46-55.
7. Lee J.H.W., Chu V.H. Turbulent jets and plumes – a Lagrangian approach. Kluwer Academic Publishers, 2003. – 390 p.