Система прогнозирования уровня инсулина на основе модели Брауна для пациентов с сахарным диабетом первого типа
Система прогнозирования уровня инсулина на основе модели Брауна для пациентов с сахарным диабетом первого типа
Аннотация
В статье исследуется метод решения задачи прогнозирования уровня инсулина у пациентов с сахарным диабетом первого типа на основе моделей Брауна первого и второго порядков. Актуальность работы обусловлена необходимостью разработки точных и адекватных систем управления гликемией для предотвращения гипо- и гипергликемических состояний. Проведены вычислительные эксперименты на реальных данных временного ряда инсулина (1182 значения), полученных с инсулиновой помпы с интервалом в 3 минуты. Для различных лагов (временных запаздываний) рассчитаны ключевые статистические характеристики (математическое ожидание, дисперсия, автокорреляция) и оценена точность прогноза. Показано, что временной ряд инсулина является стационарным, а модель Брауна первого порядка демонстрирует более стабильные результаты по сравнению с моделью второго порядка для данной задачи. Наименьшая средняя относительная ошибка прогноза (11,67%) достигнута для лага j=20 (60 минут). Разработанная программная система может быть использована как инструмент для анализа индивидуальных параметров регуляции инсулина.
1. Введение
Математическое моделирование биологических процессов представляет собой сложную многопараметрическую задачу, находящуюся на стыке медицины, биологии и информационных технологий
. Одной из важнейших практических задач в этой области является разработка систем управления гликемией для пациентов с сахарным диабетом 1 типа.Существующие системы прогнозирования уровня глюкозы и расчета доз инсулина часто не обладают достаточной точностью, что может приводить к опасным для жизни пациента состояниям — гипогликемической или гипергликемической коме
. В качестве альтернативного или дополняющего подхода рассматривается задача прямого прогнозирования необходимых доз инсулина на основе анализа его временного ряда .В последние годы наблюдается смещение исследовательского фокуса от чисто глюкозо-ориентированных предсказательных моделей к методам, напрямую учитывающим и/или оценивающим активный инсулин (Insulin-on-Board, IOB) и параметры дозирования. Так, предложены модельные оцениватели IOB на основе расширенного фильтра Калмана, использующие прямые измерения инсулина для более точной в реальном времени оценки «остаточного» действия введённых доз, что критично для предотвращения гипо- и гипергликемии
.Одновременно развиваются клинически ориентированные AI-системы титрования: в рандомизированном исследовании показано, что алгоритм AI способен обеспечивать качество инсулин-терапии, сопоставимое с врачом, что подтверждает клиническую реализуемость интеллектуальных решений в дозировании
, .Параллельно активно исследуются подходы глубокого обучения: от автоматического расчёта болюсной дозы при «необъявленных» приёмах пищи средствами (Deep Reinforcement Learning, DRL) до трансформерных и мультимодальных архитектур для персонализированного краткосрочного прогноза CGM-сигнала, что улучшает предсказуемость динамики и позволяет учитывать контекст пациента
, . В контуре управления, модельно-предиктивное управление (Model Predictive Control, MPC) с учётом длительных постнагрузочных эффектов и схемы EKF-оценивания внутренних состояний демонстрируют устойчивое повышение time-in-range и снижение риска экстремумов, что подчёркивает ценность сочетания статистической фильтрации, прогнозирования и адаптивного управления . Совокупность этих работ формирует современный ландшафт, где ключевыми тенденциями являются персонализация, явный учёт IOB и интеграция гибридных моделей (статистическое сглаживание + DL/DRL) с ориентацией на клиническую валидацию .На этом фоне предлагаемая в статье модификация модели Брауна с адаптивными параметрами и каскадным расчётом статистик занимает нишу легковесных, интерпретируемых и вычислительно экономных предсказателей временных рядов инсулина. В отличие от DL/DRL-подходов, требующих значительных массивов данных и сложной настройки, адаптивное экспоненциальное сглаживание обеспечивает прозрачность и быструю персонализацию, а явная фокусировка на IOB (по аналогии с EKF-оцениванием) делает метод релевантным текущим трендам, при этом создавая основу для гибридизации (например, инициализация/регуляризация параметров по данным из DL-моделей)
.Таким образом, новизна данного исследования заключается в модификации модели Брауна за счет адаптивных параметров и каскадного расчета статистических характеристик для заданного числа лагов, что позволяет строить индивидуально адаптирующуюся под конкретного пациента математическую модель регуляции гликемии. Целью работы является разработка и исследование программной системы, реализующей функцию прогнозирования значения инсулина на основе модели Брауна.
2. Методы и принципы исследования
В качестве источника данных для исследования использовались значения инсулина, полученные из памяти инсулиновой помпы пациента с сахарным диабетом 1 типа (см. таблицу). Исходный временной ряд состоял из 1182 измерений, проведенных с интервалом в 3±1 минуты. Погрешность измерения значений инсулина составила ±0,001 м.е.
.Таблица 1 - Часть исходных данных
№п/п | Date | Time | Carbs-1, гр. | IOB-1, м.е. | Glucose-1, мг/длитр |
0 | 2018-03-12 | 06:30:09 | 0 | -0,08 | 142 |
1 | 2018-03-12 | 06:32:03 | 0 | -0,023 | 140 |
2 | 2018-03-12 | 06:34:44 | 0 | 0,136 | 140 |
3 | 2018-03-12 | 06:37:56 | 0 | 0,197 | 140 |
4 | 2018-03-12 | 06:40:37 | 0 | 0,354 | 140 |
5 | 2018-03-12 | 06:43:25 | 0 | 0,361 | 140 |
6 | 2018-03-12 | 06:46:35 | 0 | 0,268 | 140 |
7 | 2018-03-12 | 06:48:38 | 0 | 0,272 | 138 |
8 | 2018-03-12 | 06:49:51 | 0 | 0,273 | 138 |
9 | 2018-03-12 | 06:51:55 | 0 | 0,278 | 136 |
10 | 2018-03-12 | 06:53:30 | 0 | 0,28 | 136 |
Примечание: в число измеряемых параметров входит: Date — Дата (ГГГГ-ММ-ДД), Time — Время (ЧЧ:ММ:СС), Carbs-1 — Углеводы, IOB-1 — Инсулин, Glucose-1 — Глюкоза; погрешность измерений датчика: Carbs-1 — ±1 гр., IOB-1 — ±0,001 м.е., Glucose — ±1 мг/длитр
Для анализа и прогнозирования была выбрана модель Брауна — адаптивная модель прогнозирования, основанная на методе экспоненциального сглаживания и позволяющая выделить две основные компоненты временного ряда: уровень и тренд
, , , . Использовались модели первого (линейная) и второго (квадратичная) порядков.Для модели первого порядка прогнозируемое значение рассчитывалось по формуле 1:
где:
i — текущее время; i = 1, 2, …, N, или
k — время упреждения; k=1, 2, …, N-1, или
A0, A1 — коэффициенты, поиск которых осуществляется с помощью метода наименьших квадратов , .
Для модели второго порядка использовалась формула 2:
где:
i — текущее время; i = 1, 2, …, N, или
k — время упреждения; k=1, 2, …, N-1, или
A0, A1, A2 — коэффициенты, поиск которых осуществляется с помощью метода Крамера.
В результате вывода получились следующие формулы для коэффициентов модели (формула 3):
Перед построением моделей был проведен анализ временного ряда. С помощью теста Дики-Фуллера была подтверждена стационарность ряда для всех исследуемых лагов. Анализ линейного тренда для лагов j=1, j=3, j=10 показал его отсутствие (коэффициент детерминации R2<0,3), что обусловило применение теста с константой.
В качестве оценки адекватности модели решено использовать абсолютную и относительную погрешность, вычисляет по формуле 4:
где:
∆ — абсолютная погрешность измерения,
y — значения инсулина, полученное с датчика,
где:
δ — относительная погрешность измерения,
y — значения инсулина, полученное с датчика,
Программная реализация системы была выполнена на языке Python в среде разработки PyCharm с использованием библиотек NumPy, Pandas, OpenPyXL и Tkinter. Программа позволяет загружать данные из Excel-файла, задавать количество лагов, производить каскадный расчет статистических характеристик (математическое ожидание, дисперсия, среднеквадратическое отклонение, минимум, максимум, мода, автоковариация, автокорреляция), каскадно вычислять коэффициенты моделей Брауна, выполнять прогнозирование и сохранять результаты в формате Excel.
3. Результаты и обсуждение
Были проведены вычислительные эксперименты для лагов j=1, 3, 7, 10, 20, 30, 40, 60, что соответствует прогнозированию на 3, 9, 21, 30, 60, 90, 120 и 180 минут вперед соответственно. Для каждого лага исследовались статистические характеристики и оценивалась точность прогноза.
Анализ автокорреляционной функции показал, что для малых лагов (j=1, j=3) корреляция является высокой и весьма высокой по шкале Чеддока (от -0,9 до -0,7). С увеличением лага корреляция ослабевала, начиная с 50-го сдвига для j=1 и с 5-9-го сдвига для больших лагов, она классифицировалась как слабая (~0,3 – 0,1) и умеренная (~0,5 – 0,3). Однако на больших сдвигах (например, после 950-го для j=1) наблюдался повторный рост корреляции, что может быть связано с циклическими суточными колебаниями уровня инсулина. Точность прогнозирования оценивалась по средней относительной ошибке. Наилучшие результаты показала модель Брауна первого порядка. Ее средняя относительная ошибка варьировалась от 11,67% (для j=20) до 22,5% (для j=30). Модель второго порядка продемонстрировала признаки переобучения, особенно на малых лагах (j=1, j=3), где ее средняя относительная ошибка достигала высоких значений, что делает ее непригодной для практического использования в данной конфигурации. Для лагов j=7, j=10, j=20, j=30, j=40, j=60 ошибка модели второго порядка была сопоставима или незначительно превышала ошибку модели первого порядка.
Причина лучшей работы модели первого порядка заключается в том, что простая линейная структура позволяет избежать избыточного подстраивания под случайные колебания ряда. Модель второго порядка пыталась аппроксимировать шум как закономерность, что приводило к завышению прогноза и росту ошибки. Таким образом, природа ошибок связана с избыточной чувствительностью более сложной модели к локальным флуктуациям, тогда как модель первого порядка лучше отражает общую динамику процесса.
На рисунке 1 представлен график коэффициента корреляции Пирсона для лага j=1, иллюстрирующий высокую степень зависимости между соседними измерениями при малом временном запаздывании.
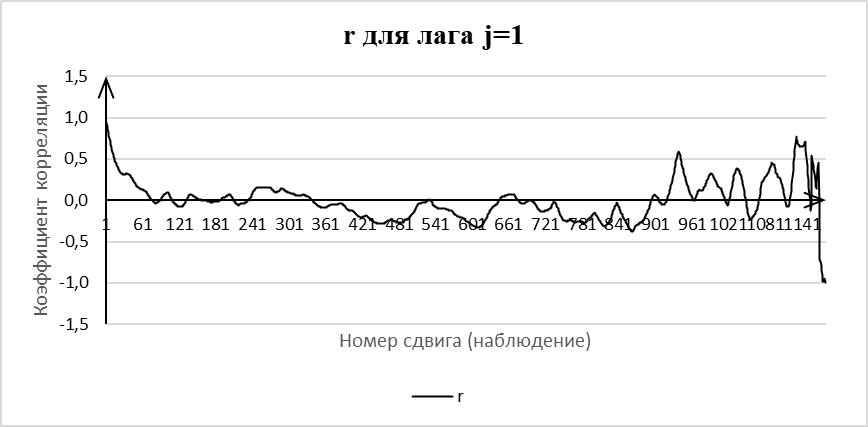
Рисунок 1 - График коэффициента корреляции Пирсона для временного ряда инсулина
Примечание: лаг j=1
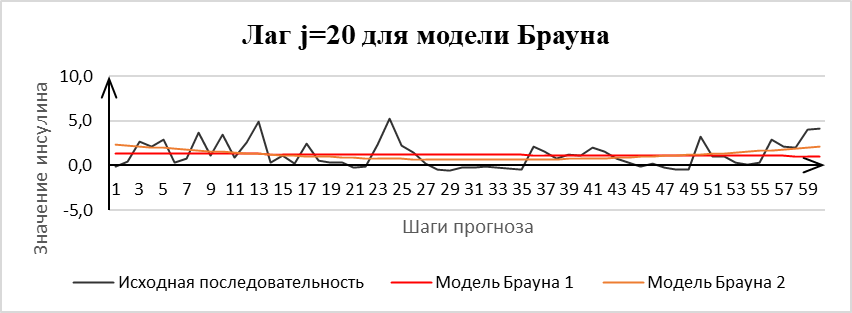
Рисунок 2 - График исходных и прогнозных значений инсулина
Примечание: модель Брауна 1-го и 2-го порядка, лаг j=20
4. Заключение
В результате работы была разработана и реализована программная система для прогнозирования уровня инсулина на основе модели Брауна. Проведенные вычислительные эксперименты на реальных данных показали, что временной ряд инсулина является стационарным и обладает выраженной автокорреляционной зависимостью на малых лагах. Наилучшая точность прогноза была достигнута с использованием модели Брауна первого порядка для лага j=20 (60 минут), средняя относительная ошибка составила 11,67%. Модель второго порядка склонна к переобучению на данных данной природы и показала неудовлетворительные результаты для краткосрочного прогнозирования.
Перспективы дальнейших исследований связаны с интеграцией в модель дополнительных физиологических параметров (уровень глюкозы, прием углеводов, физическая активность), использованием гибридных моделей (например, сочетание модели Брауна с нейронными сетями), а также проведением клинических испытаний для валидации системы на более обширных выборках данных.
