МОДЕЛИРОВАНИЕ И ПРОГНОЗИРОВАНИЕ ЭФФЕКТИВНОСТИ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА В УНИВЕРСИТЕТЕ
МОДЕЛИРОВАНИЕ И ПРОГНОЗИРОВАНИЕ ЭФФЕКТИВНОСТИ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА В УНИВЕРСИТЕТЕ
Аннотация
Система высшего образования динамично развивается с каждым годом, что приводит к естественному конкурированию вузов друг с другом. Одной из компонент оценивания деятельности университета является оценка качества предоставляемого образования. Высокие показатели, попадание в авторитетные рейтинги напрямую зависят от количества выпускников и качества их профессионализма.
В работе будет рассмотрена математическая модель повышения эффективности образовательного процесса при реализации факультативных дисциплин на примере реальных данных. В ходе исследования определена вероятность окончания вуза студентами, а также проведён сравнительный анализ применения моделей машинного обучения в процессе прогнозирования.
Также в статье представлены результаты численного моделирования, полученные при использовании языка программирования Python и дополнительных библиотек анализа данных.
1. Введение
Относительно большое количество студентов не получают диплом об образовании в процессе обучения в вузе
. Это касается не только студентов Российской Федерации, но и стран Европы и США. Причин этому явлению несколько. Самой основной и распространённой является академическая неуспеваемость студентов, которая может возникнуть не только по причине отсутствия знаний по какому-либо предмету, но и из-за систематических нарушений учебной дисциплины. Еще одним фактором являются жизненные обстоятельства, которые включают в себя изменение места жительства, социального статуса, семейного положения и т. д.Система высшего образования в целом ориентирована на обеспечение высокого образовательного стандарта. Для достижения этой цели необходим строгий административный подход. Разработка образовательных программ, набор абитуриентов, кадровое и материально-техническое обеспечение, финансы и т. д. Однако именно успешная обучаемость студентов является основным показателем эффективности работы высших учебных заведений. Именно она служит главным критерием для оценки качества учебного процесса. В связи с этим одной из важных проблем является анализ причин, влияющих на отчисление, а также прогнозирование успешного окончания вуза
.С целью расширения научного кругозора, улучшения качества прикладных знаний студентов, во многих вузах реализуются дополнительные факультативные дисциплины по выбору. Данная форма занятий является относительно гибкой как с точки зрения методики, так с точки зрения и содержания. Это может быть классическое занятие, например, лекция или семинар, а может и свободная дискуссия. Выборность реализуется в начале каждого семестра и осуществляется по установленным университетом правилам. Однако существует такая проблема, как неоптимальное использование выделенных бюджетных средств вуза на реализацию спецкурсов, так как определенное количество студентов, изъявивших желание посещать курс, так его и не оканчивают. Причины этого могут быть различны. Важно отметить, что в предложенной модели факультатив представляет собой особый вид занятий (с применением различных педагогических технологий).
На данный момент существует достаточное количество моделей, описывающих те или иные процессы обучения, эффективности, оптимизации и т.д. С изменением образовательной среды менялись и актуальные методы автоматизированного анализа данных в образовательных системах. Так, в работах
, , , представлены математические модели и методы моделирования показателей эффективности деятельности вуза. В научных трудах , рассматривались сущности прогнозирования результатов обучения, основанные на корреляционном, регрессионном, кластерном и факторном анализах. Кроме этого, с помощью автоматизированного системно-когнитивного анализа и его программного инструментария – интеллектуальной системы «Эйдос» в монографии была изучена зависимость учебных достижений студентов университета от их занятий в учебном подразделении в период обучения в средней школе и от результатов ЕГЭ. Данный метод является достаточно обоснованным и хорошо изученным в основе которого эффективная модель, относящаяся к нечетким декларативным гибридным моделям.В новых исследованиях широко используются методы EPM (Education Process Mining) и машинного обучения (Machine Learning – ML) с целью анализа образовательных данных
.2. Постановка задачи
В связи с вышеизложенным была создана математическая модель прогнозирования эффективности образовательного процесса в вузе с учетом применения дополнительных образовательных технологий.
Для достижения поставленной цели необходимо решить следующие задачи:
– создание оптимизационной модели на основе машинного обучения для прогнозирования вероятностей окончания университета по заранее выбранным метрикам качества;
– сравнительный анализ уравнений регрессии (логистическая, гребневая, Лассо);
– численное моделирование алгоритма с оптимальным уравнением регрессии при использовании языка Python;
– вывод об оптимальности использования регрессионных соотношений с точки зрения точности прогноза.
3. Основные результаты
Пусть в университете обучается студентов. Обозначим за
множество тех студентов, кто принял решение записаться на дополнительные дисциплины:
. Количество записавшихся на дополнительные дисциплины студентов будет равно мощности множества
, то есть
Введём понятие рейтинга вуза, под которым будем понимать оценку деятельности образовательного учреждения на основании различных учебных активностей и мероприятий. Понятно, что общий (интегральный) рейтинг – линейная комбинация частных (), взятых с априори заданными весовыми коэффициентами.
В данной работе рассмотрим частный рейтинг вуза на основании организации факультативных дисциплин. Пусть он будет вычисляться как произведение количества студентов и вероятностей их выпуска
:
На реализацию одной дополнительной дисциплины университет выделяет рублей. Под
понимается количество затраченных средств на использование образовательных технологий для j-го студента (в предложенной постановке это факультативные занятия). Тогда основной целью для вуза будет повышение вероятности выпуска студентов при минимизации затрат на обеспечение. Постановка задачи принимает вид линейного программирования при ограничениях:
Примем во внимание тот факт, что число мест на каждом курсе ограничено, то есть мощность множества студентов на факультативе не превосходит наперед заданного числа: .
В данной постановке существует два сценария:
– любой студент может записаться на дополнительный понравившийся курс;
– выбор курса предоставляется лицам с вероятностью окончания университета не менее 0,5.
Для проверки эффективности и адекватности модели были проведены вычисления, в ходе которых была рассмотрена группа из 100 студентов, охватывающая 63 различных факультатива. Количество участников на каждом курсе не превышало 30. Стоимости курсов варьировались в пределах 2000-2500 евро, стоимость обеспечения техникой
в пределах 15-150 евро соответственно.
Получены значения функционала равны
при произвольной вероятности окончания университета и
при вероятности участия на курсе только тех студентов, у кого .
На основании полученных результатов можно сделать вывод о целесообразности записи на факультативы только студентов с относительно высоким уровнем обученности.
Далее в исследовании прогнозируется вероятность окончания высшего учебного заведения на реальном открытом наборе данных, предоставленным отделом академических услуг Политехнического университета Порталегре
. Здесь учитывается фактор дополнительных образовательных технологий, в том числе и в форме дополнительных занятий со студентами с применением различных методик.4. Описание исследуемых данных
Набор данных включает в себя демографические, социально-экономические и макроэкономические сведения, известные на момент зачисления студентов, а также текущие результаты окончания первого и второго семестров, собранные за период с 2008 по 2019 учебный год. Данные представлены в виде табличного текстового файла CSV, содержащего 3630 строк по 35 столбцов в каждой.
В выборке известны апостериорные вероятности статуса студента, принимающие два возможных значения . Анализируя исходные данные установлено, что 1421 учащихся были отчислены, а 2209 продолжили своё обучение (см. рисунок 1).
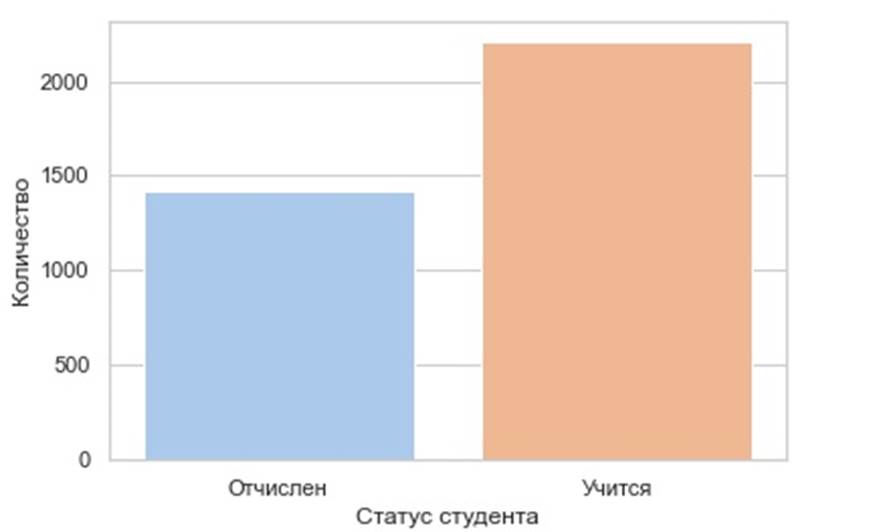
Рисунок 1 - График распределения студентов
5. Отбор факторов (образовательных технологий) и методы построения множественной регрессии
Для успешного прогнозирования вероятностей необходимо установить функциональную связь между зависимыми переменными – вероятностями окончить университет, для которых применяется соответствующая образовательная технология, и группой независимых переменных
– количествами студентов, для которых применяется соответствующая образовательная технология, с учётом ошибки модели
– случайной величины, характеризующей отклонения результативного признака от теоретического, найденного по уравнению регрессии:
В данном случае рассматриваются три часто используемые модели машинного обучения: логистическую, гребневую и Лассо регрессию. В дальнейшем необходимо провести сравнительных анализ их применения к выбранным данным.
1) В логистической регрессии рассматривается модель следующего вида:
где – сигмоидная функция. Для определения коэффициентов регрессии используется метод максимального правдоподобия. Тогда функция минимизации принимает следующий вид:
В качестве метода поиска экстремума применяется градиентный спуск, в котором пересчитываются веса по формуле , где
– шаг градиента.
2) В гребневой регрессии рассматривается линейная зависимость . При этом накладываются ограничения на величину коэффициентов
:
. Минимизирующий функционал
с учётом ограничений принимает вид:
где – неотрицательный параметр. Решением в этом случае будет вектор
, где
– диагональная матрица, называемая гребнем.
3) В регрессии Лассо используется другое ограничение на коэффициенты :
. Положительным моментом использования
нормы является не только осуществление регуляризации, но и приравнивание некоторых коэффициентов
к нулю при достаточно большом значении
. Минимизирующий функционал такой же, как и в гребневой регрессии.
Для сравнения и оценки качества применимы следующие метрики:
– среднеквадратическая ошибка
– средняя абсолютная ошибка
– коэффициент детерминации
Для реализации численного моделирования использовался язык программирования Python в совокупности с библиотекой машинного обучения Scikit-learn. Выборка данных была предварительно разделена на обучающую и тестовую в соотношении 7:3. В результате проведения экспериментов были получены результаты, представленные в таблице 1. Наилучшие показатели в рамках текущей постановки задачи продемонстрировала логистическая регрессия.
Кривая обучения модели в зависимости от объёма обучающего набора данных представлена на рисунке 2.
Таблица 1 - Результаты численного моделирования множественной регрессии
Оценка | Модель | ||
Логистическая регрессия | Гребневая регрессия | Лассо регрессия | |
RMSE | 0,2486 | 0,2777 | 0,2957 |
MAE | 0,1301 | 0,2002 | 0,2179 |
R2 | 0,6407 | 0,6776 | 0,6344 |
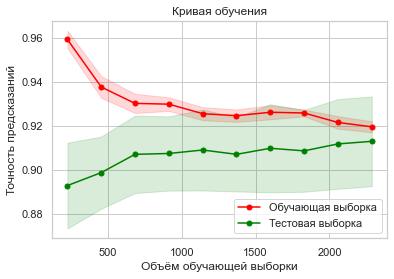
Рисунок 2 - График обучения модели логистической регрессии
= [0,2974 – 0,0336 – 0,0278 – 0,1090 – 0,3350 0,0197
0,0127 – 0,0118 0,0097 0,0526 – 0,0036 – 0,2874
– 0,0351 – 1,3053 2,1876 – 0,3922 0,8138 – 0,0362
0,1512 – 0,1962 – 0,2975 – 0,0040 0,6590– 0,1134
0,0969 – 0,2003 – 0,6431 – 0,0303 0,9486 0,1063
0,2569 – 0,0763 0,0101 – 0,0087]
Существенность полученных коэффициентов определяется отношением , где
– коэффициент множественной регрессии;
– среднее квадратическое отклонение этого коэффициента. Если
, взятого по таблицам t-распределения Стьюдента, то с заданной вероятностью не отвергается гипотеза, что соответствующий коэффициент регрессии в генеральной совокупности приравнивается к нулю. При этом i-й фактор в таком случае признаётся несущественным для построения регрессионного уравнения. Если при проведении исследования оказывается, что вычисленные значения
для нескольких факторов не превышают
, то факторы исключаются поочередно, начиная с наименьшего по абсолютной величине
. Процесс исключения происходит до тех пор, пока не будет выполняться соотношение
.
При уровне значимости было установлено, что вектор весовых коэффициентов можно сократить до 9 факторов, вместо предполагаемых 34 с незначительной потерей качества
, с заметным упрощением модели, а также уменьшением мультиколлинеарности в наборе данных между сильно коррелированными признаками.
6. Практический аспект
Модель прогнозирования эффективности образовательного процесса может быть использована для определения того, какие методы и подходы в образовании наиболее эффективны в процессе достижения желаемых целей. Например, она может помочь школам и университетам определить, какие курсы и программы наиболее успешны, а также какие учебные материалы и методы преподавания наиболее эффективны.
Представленная модель может быть использована для прогнозирования будущих результатов обучения студентов, на основе их текущих оценок В этом случае преподавателям и администрации образовательных учреждений можно будет определить, какие студенты нуждаются в дополнительной поддержке и помощи, чтобы достичь успеха в учебе.
Кроме того, появляется возможность анализа данных об успеваемости и приоритетных направления для студентов (на основе выборности дополнительных дисциплин). Это дает возможность образовательным учреждениям разрабатывать более эффективные стратегии обучения и улучшать качество образования.
В целом модель прогнозирования эффективности образовательного процесса является востребованным инструментом для улучшения качества образования и достижения лучших результатов в учебе.
7. Заключение
В ходе качественного анализа сравнения моделей машинного обучения для отсеивания студентов был реализован алгоритм логистической регрессии, показавший хорошие результаты на практике. Предложенный подход универсален и может использоваться в любом учреждении высшего или специального профессионального образования. Применение модели поможет выявить основные причины отчисления обучающихся и скорректировать работу вуза в дальнейшем. Разработанная модель послужила методической основой для реализации общеуниверситетских факультативных дисциплин, где возможность записи на курс будет вычисляться на основе полученных вероятностей. Результаты данного исследования имеют практическую значимость для лиц, принимающих управленческие решения о формировании стратегии развития и конкурентоспособности высших учебных заведений в условиях ограниченного бюджета.
Тем не менее выбранный подход не является совершенным. В дальнейшем планируется улучшение используемой модели с учетом методики выбора дополнительных занятий, а также применением дополнительных технологий. Модель не рассчитана на прогноз относительно основных дисциплин, что также будет учитываться в дальнейшей работе над ней.
Программный код опубликован в Интернет-репозитории .
