РАСЧЕТ K+/Nа+ СЕЛЕКТИВНОСТИ В ВОДНОЙ ПОЛОСТИ K+ КАНАЛА ПО КЛАССИЧЕСКОЙ ФОРМУЛЕ БОРНА

Проблема моделирования катионной избирательности в водной полости (ВП) в K+ канале

В [1] было показано, что в центре бактериального Kcsa K+ канала находится ВП. Статья [1] обсуждалась в монографии [2] по ионным каналам в биологических мембранах, также в ней рассматривалось применение формулы Борна к анализу рядов селективности Эйзенмана. В [3] было показано, что в ВП существует не только в Kcsa K+ канале, но и в других калиевых каналах.

В [4], [5], [6], [7] для моделирования ВП K+ канала применялись различные теории. В [4] была использована классическая электростатика для моделирования электростатической стабилизации катиона K+ в ВП, в [5] использовались расчеты с помощью квантовой механики. В работах [6], [7] для рассмотрения катионной избирательности канала использовалась теория нелокальной электростатики (НЭТ). Так в [6] НЭТ использовалась для расчета катионной избирательности в ВП канала в предположении об изменении корреляционной длины воды в ВП по сравнению с ее значением в наружном растворе. В [7] был проведен расчет K+/Na+ селективности К+ канала, обусловленной селективным фильтром канала. Обзор методов НЭТ можно найти в монографии [8]. НЭТ имеет достаточно сложный математический аппарат, что определяет целесообразность проведения анализа катионной избирательности ВП канала с помощью более простых для восприятия биологов классических электростатических подходов.

Величина катионной избирательности K+ канала определяется его селективным фильтром [1], [2], [3]. ВП канала также должна обладать некоторой катионной избирательностью, меньшей, по сравнению с катионной избирательностью с селективного фильтра. В противном случае некоторая часть центральных полостей K+ каналов была бы быть заполнена катионами Na+, которые являлись бы блокаторами для движения катионов K+ через канал. Это также отмечалось в работе [6], в которой для расчета селективности K+ канала методами нелокальной электростатики предполагалось увеличение корреляционной длины воды в полости с учетом того, что статическая диэлектрическая проницаемость в полости такая же как в наружном растворе.

В настоящей работе K+/Na+избирательность полости рассчитывается методами классической теории ионной сольватации, основанной на формуле Борна.

В рамках классической теории ионной сольватации, развитой М. Борном, электростатическая составляющая энергии сольватации в наружном растворе , рассчитывается по формуле (1) для локальной среды со статической диэлектрической проницаемостью :

(1)

Энергия гидратации иона в наружном растворе для катионов и в данной работе будет вычисляться по классической формуле Борна (1), в которой – заряд электрона. В формуле (1) – радиус сферы, на которой находится весь заряд иона в модели Борна.

Диэлектрическая проницаемость в сферической полости значительно меньше величины 80 для объемной воды и составляет около 5, как это показывает расчет методами молекулярной динамики для воды в сферической полости [9]. В [10] при анализе диэлектрических свойств воды в порах биологических мембран также отмечалось резкое уменьшение диэлектрической проницаемости. Поэтому энергии гидратации ионов в центре водной полости, окруженной белковыми «стенками» также будет вычисляться по классической формуле Борна (2), но со статической диэлектрической проницаемостью воды в полости , которая меньше, чем :

(2)

На рис. 1 представлены результаты расчета энергий гидратации катионов и , находящихся в центрах водных полостей каналов, окруженной белками.

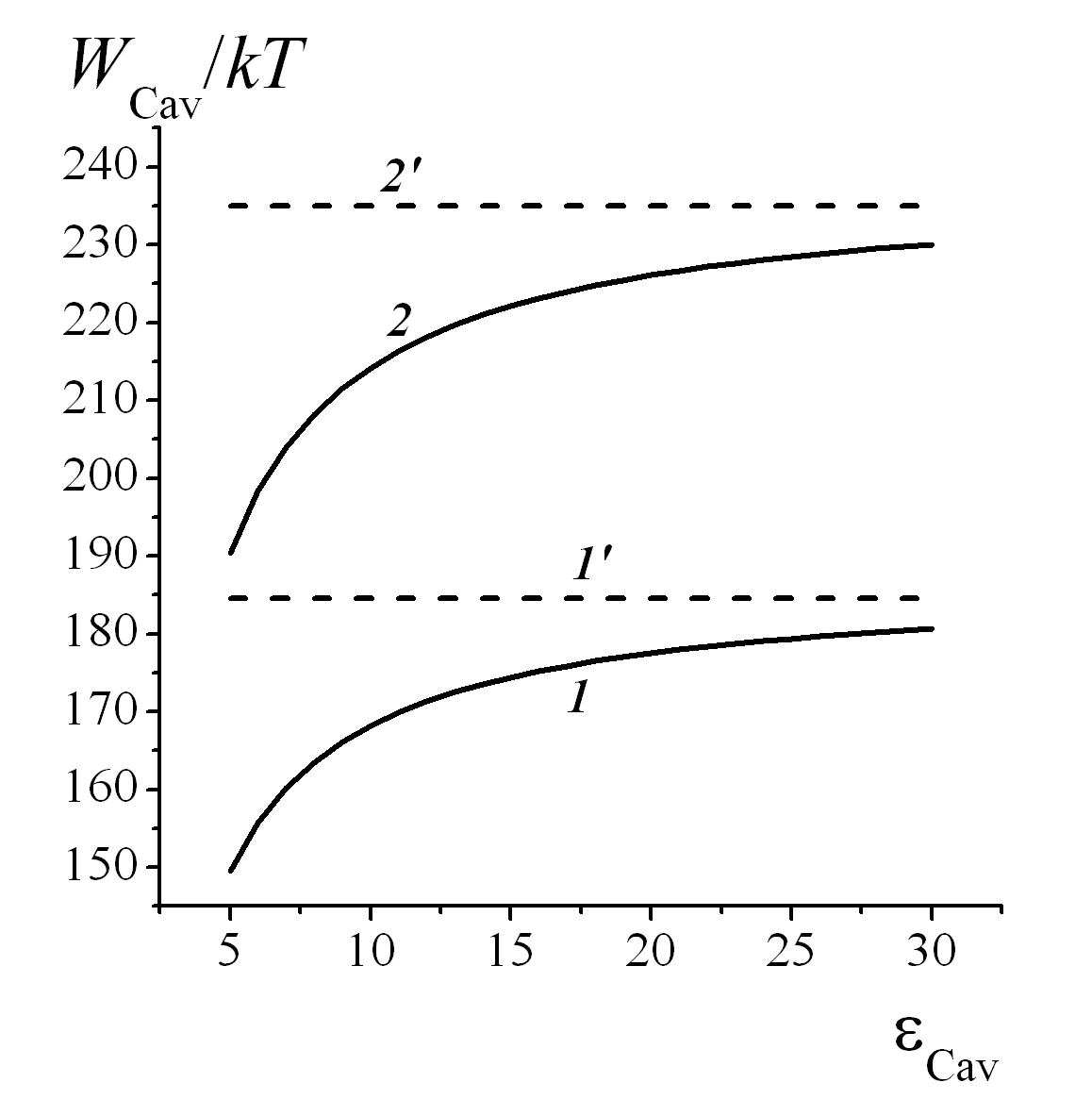
Рисунок 1 - Энергии гидратации WCav(rK) и WCav(rNa) катионов K+ и Na+ в водных полостях каналов в зависимости от диэлектрической проницаемости εСav в полости

DOI:10.23670/IRJ.2022.125.8.1

По оси ординат: (сплошная кривая 1) и (сплошная кривая 2) в единицах , рассчитанные по формуле (2). По оси абсцисс: диэлектрическая проницаемость в полости. Штриховыми прямыми 1' и 2' представлены энергии гидратации катионов и в наружном растворе, рассчитанные по классической формуле Борна (1). Радиусы и взяты по шкале работы [11]: .

Поскольку в полости , то . Поэтому энергия гидратации катиона , находящегося в полости меньше ее значения в наружном растворе, рассчитанного по формуле (1), и равного (штриховая прямая 1' на рис. 1). Энергия гидратации катиона в полости, также меньше ее значения, рассчитанного по (1) при .

Изменение энергии гидратации иона при его переходе в полость канала в классической электростатике рассчитывается по формуле (3), которая следует из формул (1)-(2). При этом изменение стандартного химического потенциала иона равно изменению его энергии гидратации, взятому с обратным знаком:

(3)

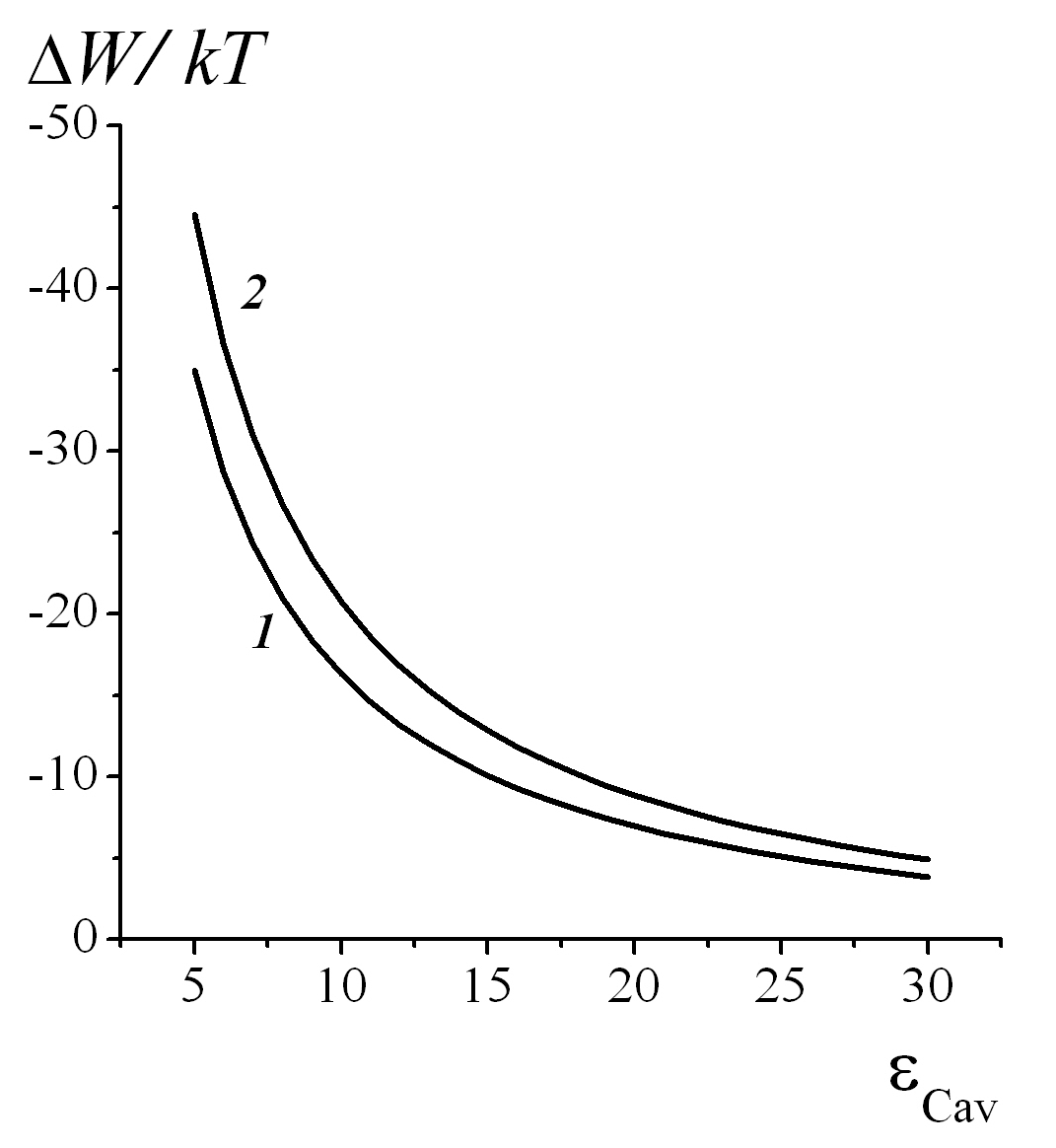
Рисунок 2 - Изменения энергий сольватаций ΔWi(εСav) катионов K+ и Na+ при переходе этих ионов в водную полость канала из свободного раствора в зависимости от диэлектрической проницаемости εСav в полости (по оси абсцисс)

Примечание: по оси ординат представлены ΔWK(кривая 1) и ΔWNa (кривая 2) в единицах kT, рассчитанные по формуле (3)

DOI:10.23670/IRJ.2022.125.8.2

Изменение энергии гидратации (1) при его переходе в полость канала с пониженной диэлектрической проницаемостью меньше, чем для катиона , как это видно из рис. 2. Этот результат является следствием различия радиуса этих катионов, и, как будет показано далее, определяет появление катионной селективности полости канала.

Энергия сил изображения , действующая на ион, находящийся в центре сферической ВП рассчитывается по формуле (4), в которой – радиус полости, а и – диэлектрические проницаемости белкового окружения полости и воды в полости соответственно:

(4)

Величина зависит от радиуса полости, но не зависит от радиуса иона, в отличие от энергии гидратации. Классическая формула (4) использовалась в [4] при анализе электростатической стабилизации катионов в водной полости канала. Однако в [4] расчет по формуле (4) проводился только при , при этом считалось, что радиус полости равен . Выбор таких большие значений диэлектрической проницаемости в полости малого размера не соответствует данным работ [9-10], как это отмечалось выше.

Нелокально-электростатический аналог формулы (4) был получен в нашей работе [12]. Учет нелокально-электростатических эффектов в полости приводит к уменьшению энергии сил изображения, действующих на катион в полости вследствие уменьшения эффективной диэлектрической проницаемости воды в полости, как это было показано в [12]. Качественно понятнее варьировать некоторую эффективную диэлектрическую проницаемость в полости εСav и рассчитывать по формуле (4) . Результаты этих расчетов представлены на рис. 3, из которого видно, что при энергия сил изображения равна нулю.

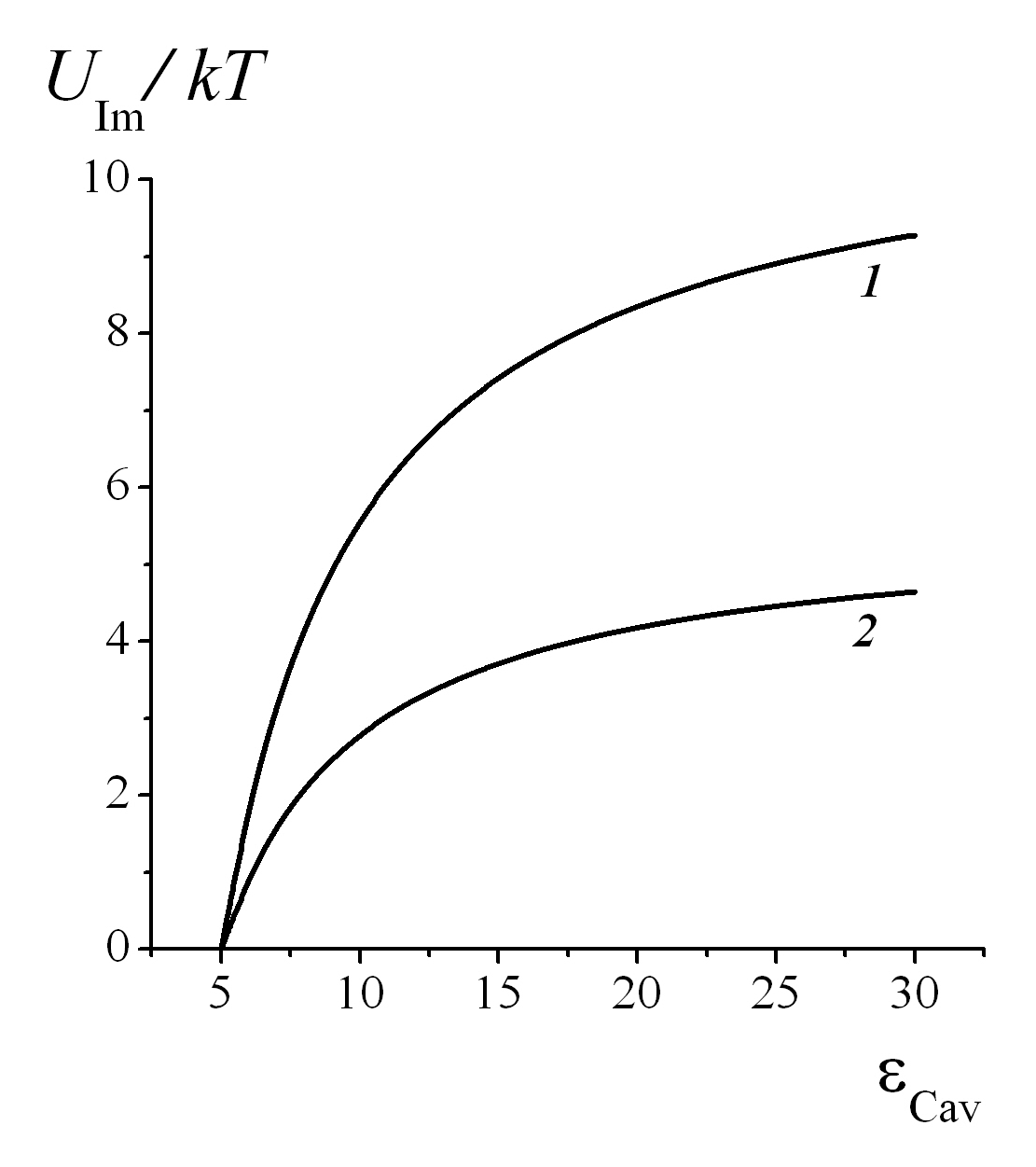
Рисунок 3 - Изменения энергий сил изображения UIm, действующих на ион, находящийся в центре сферической ВП канала в зависимости от диэлектрической проницаемости εСav в полости

DOI:10.23670/IRJ.2022.125.8.3

По оси ординат: в единицах , рассчитанные по формуле (4), и представленные сплошными кривыми и для двух значений радиусов полости . По оси абсцисс: диэлектрическая проницаемость в полости. Диэлектрическая проницаемость белкового окружения полости выбрано при расчете по (4) выбрано 5.

Получим выражение (5) для изменения свободной энергии Гиббса при переходе катиона из свободного раствора в полость канала, используя формулы (3)-(4). Расчет по формуле (5) приведен на рис. 4.

(5)

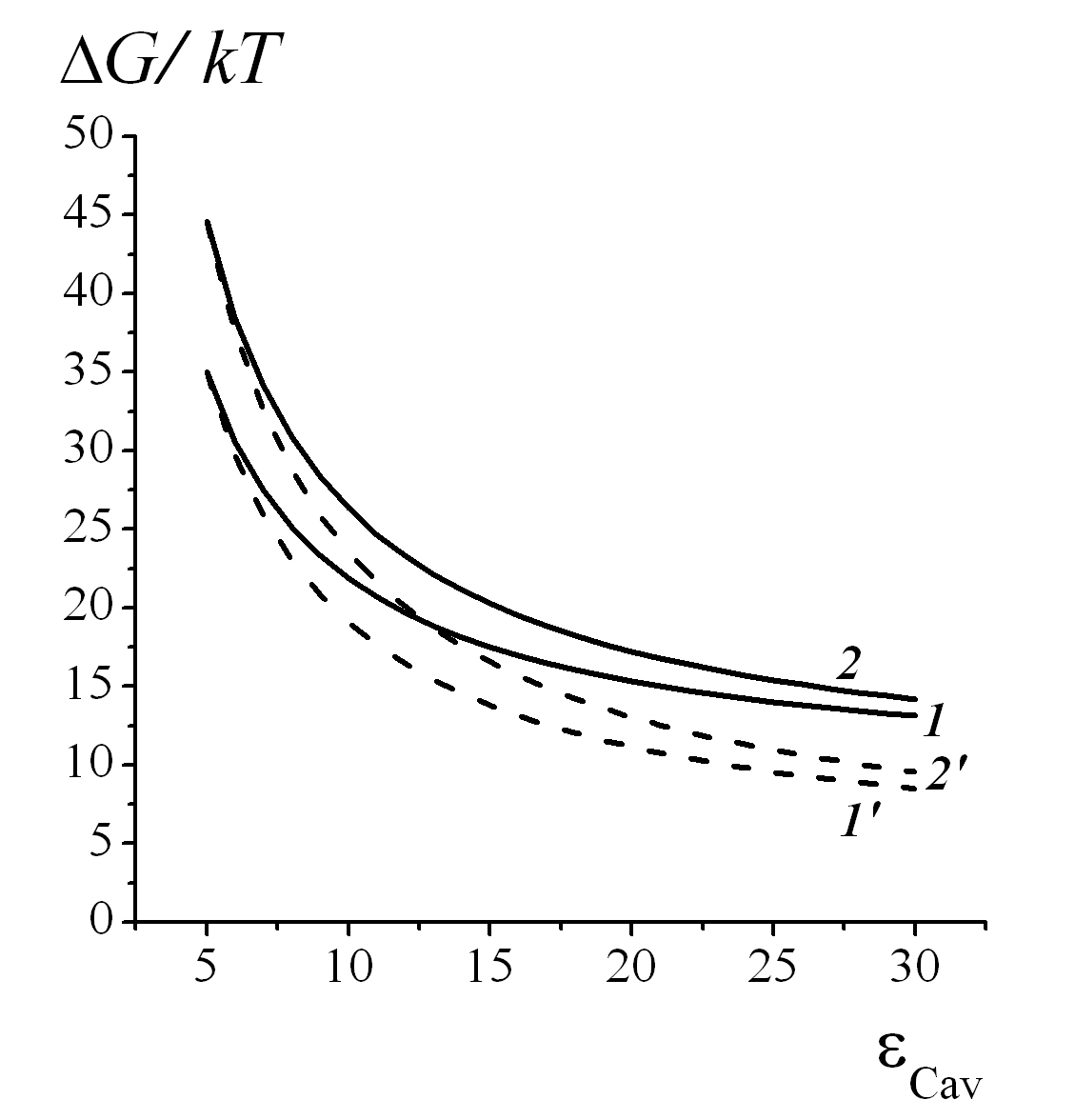
Рисунок 4 - Изменения свободной энергии Гиббса ΔG катионов K+ и Na+ при их переходе в ВП канала из свободного раствора в зависимости от диэлектрической проницаемости εСav в полости (ось абсцисс)

DOI:10.23670/IRJ.2022.125.8.4

По оси ординат: и в единицах , представленные сплошными кривыми 1 (для )  и 2 (для ) для радиусов полости и штриховыми кривыми 1' (для ), 2' (для ) при (расчет по формулам (5)). При расчете диэлектрическая проницаемость белкового окружения полости выбрано равной 5. Как это видно из рис. 4, рассчитанные величины слишком большие, чтобы катион мог войти в полость, и это обстоятельство является проблемой при расчетах по классической теории Борна. Эта проблема возникает потому, что величина стандартного химического потенциала иона в наружном растворе, рассчитанная по классической формуле Борна, значительно превышают ее экспериментальное значение. Поэтому первый член формулы (5) намного больше реального изменения химического потенциала. Для решения этой проблемы в наружном растворе надо рассчитывать по формулам нелокальной электростатики (см. монографию [8]), как это отмечалось в [7].

Приведем формулы коэффициентов распределения катионов и между ВП ионного канала и свободным раствором, нужные для расчета катионной избирательности в полости, вывод которых приведен в [6]:

(6)

Третьи слагаемые в (6) описывают электростатическое взаимодействие иона в полости с заряженными или дипольными группами белков, окружающих полость: , где – электростатический потенциал в центре полости. При расчете величины избирательности в ВП второй и третий член в экспоненте (6), сокращаются, а остаются только изменения стандартных химических потенциалов катионов и :

(7)

Подставляя в (7) из формулы (3), получим выражение, описывающее зависимость селективности от диэлектрической проницаемости в полости:

(8)

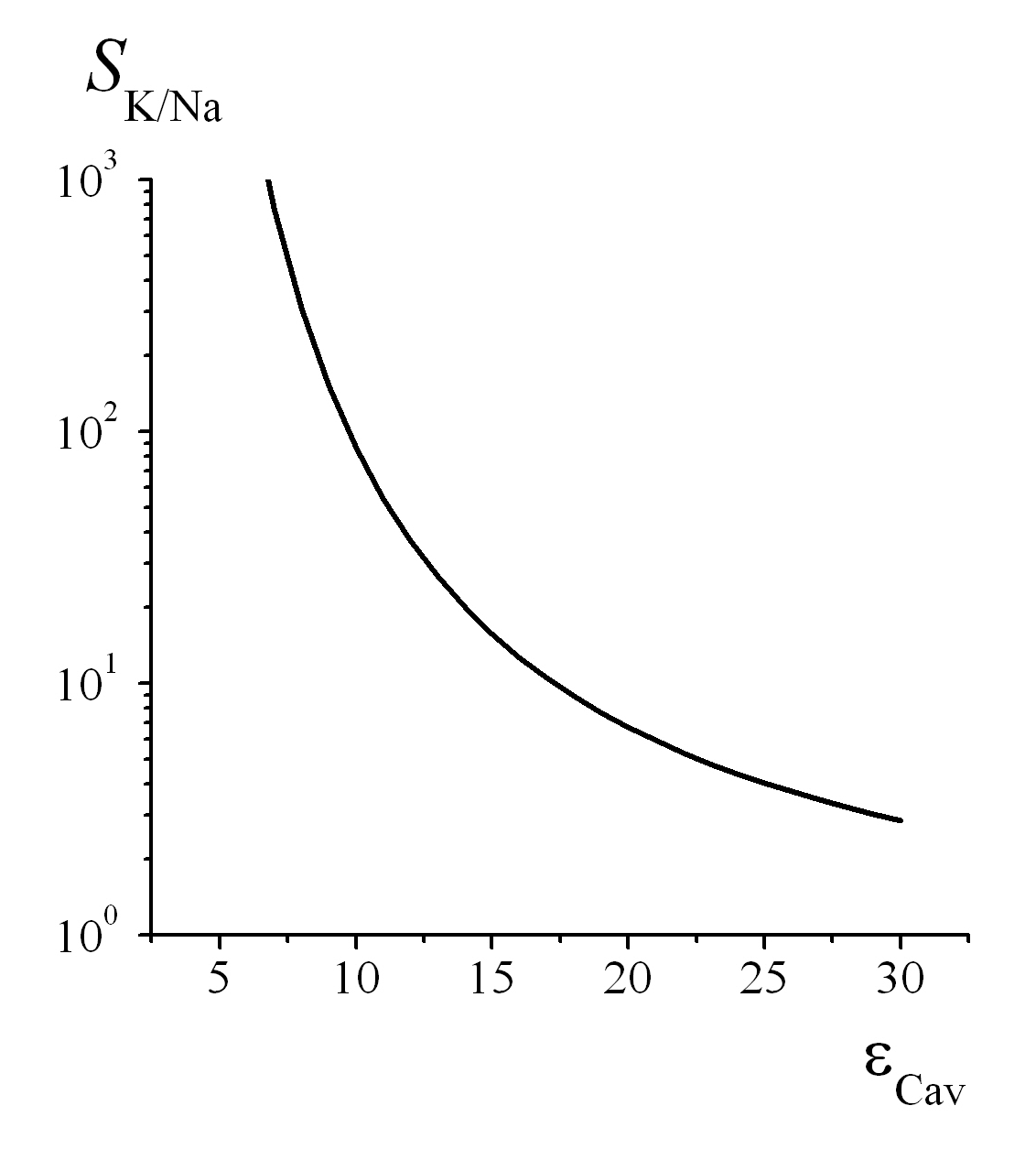
Рисунок 5 - K+/Na+ избирательность SK/Na в ВП в зависимости от диэлектрической проницаемости εСav в полости

DOI:10.23670/IRJ.2022.125.8.5

По оси ординат: избирательность водной полости канала. По оси абсцисс: диэлектрическая проницаемость в полости. Радиусы и взяты по шкале работы [10]: , .  

Формула (8) представляет основной результат развитой теории катионной селективности ВП канала, а на рис. 5 приведен расчет величины по этой формуле.

Формула (8) предсказывает существование селективности в водной полости канала для любых значений диэлектрической проницаемости в полости, как это видно из рис. 5. Однако этот метод, основанный на расчете энергий сольватаций ионов по классической формуле Борна, не может быть применим к объяснению возникновения селективности в ВП канала. Поскольку , то под экспонентой в формуле (8) оказываются два положительных сомножителя . Поэтому величина больше единицы, а это значит, что на основании формулы (8) можно объяснить только избирательность в полости канала. Эту проблему можно решить, воспользовавшись методом, развитым в работе [7], в которой рассматривался селективный фильтр канала, а не его ВП. В этой работе энергии гидратации катионов в объемном растворе рассчитывались не по классической формуле Борна, как в данной статье, а по формулам НЭТ [8]. На этой основе в [7] была объяснена возможность перехода от к селективности. Вероятно, этот НЭТ метод может быть использован и для расчета селективности в водной полости канала.

Еще одним недостатком расчета, основанного на классической электростатике, является слишком большие рассчитанные значения величины , когда диэлектрическая проницаемость в полости меньше 7 (см. рис. 5), то есть как раз при тех значениях, которые имеют в полостях радиуса порядка нанометра [9], [10]. Как известно [2], большие значения селективности канала создаются селективным фильтром, а не водной полостью. Причиной указанного недостатка классической модели является использование формулы (1) для расчета энергии гидратации ионов в объемном растворе, расчет по которой дает величины большие, чем экспериментальные значения.  Следует ожидать, что при использовании формул нелокальной электростатики для расчета энергий гидратации и вместо формулы (1), этот недостаток приведенной здесь классической модели будет устранен.

Главный вывод заключается в том, что расчет по классической теории гидратации предсказывает существование селективности водной полости канала (см. рис. 5), если при расчете учитывать, что диэлектрическая проницаемость воды в полости канала меньше ее значения в объеме раствора. Этот расчет показывает, что катионная избирательность обусловлена различием радиусов ионов. Однако расчет по классической формуле Борна не может объяснить стабилизацию катионов в водной полости канала. Причина этого в том, что классическая электростатика приводит к сильно завышенным значениям энергии гидратации ионов по сравнению с их экспериментальными величинами. По этой причине при анализе стабилизации катионов в водной полости канала надо использовать более сложные теории. Однако для качественного понимания возникновения селективности водной полости канала расчет по формуле Борна полезен, поскольку он объясняет возникновение селективности из-за различия радиусов катионов. Приведенные в данной работе результаты указывают один из возможных методов дальнейшего развития теории катионной селективности в каналах. Это использование НЭТ для расчета энергий гидратации ионов.