МЕТОД L-КРИВОЙ ДЛЯ ОЦЕНИВАНИЯ ОПТИМАЛЬНОГО ПАРАМЕТРА СГЛАЖИВАЮЩЕГО КУБИЧЕСКОГО СПЛАЙНА

МЕТОД L-КРИВОЙ ДЛЯ ОЦЕНИВАНИЯ ОПТИМАЛЬНОГО ПАРАМЕТРА СГЛАЖИВАЮЩЕГО КУБИЧЕСКОГО СПЛАЙНА

Научная статья

Воскобойников Ю.Е.^1, *, Боева В.А.²

¹ ORCID: 0000-0002-5282-6002;

² ORCID: 0000-0002-5668-3416;

^{1, 2} Новосибирский государственный архитектурно-строительный университет, Новосибирск, Россия;

¹ Новосибирский государственный технический университет, Новосибирск, Россия

* Корреспондирующий автор (voscob[at]mail.ru)

Аннотация

Универсальным аппаратом для фильтрации измерительных шумов является сглаживающий кубический сплайн дефекта единица. Величина ошибки фильтрации (сглаживания) в существенной степени определяется значением параметра сглаживания. При значении параметра сглаживания, называемым оптимальным, величина ошибки сглаживания принимает минимальное значение. На практике априорная информация о точных (не зашумлённых) значениях сигнала отсутствует, и вычислить значение оптимального пара сглаживания невозможно. В связи с этим используемые для решения практических задач алгоритмы выбора оптимального параметра позволяют оценить лишь приемлемые ошибки сглаживания, которые порой в значительной степени превышают минимальные значения. Особую трудность представляет оценивание оптимального параметра сглаживания при неизвестной дисперсии шума измерения экспериментальных данных. В данной работе строится и подробно исследуется алгоритм оценивания оптимального параметра на основе метода L-кривой. Этот метод используется для выбора параметра регуляризации в алгоритмах решения некорректно поставленных задач. Особое внимание уделяется оцениванию оптимального параметра в условиях коррелированного шума. По результатам этих исследований даются практические рекомендации по применению этого алгоритма выбора в практике обработки экспериментальных данных.

Ключевые слова: фильтрация шумов, сглаживающий кубический сплайн, параметр сглаживания, выбор параметра при неизвестной дисперсии шума.

L-CURVE METHOD FOR EVALUATING THE OPTIMAL PARAMETER OF A SMOOTHING CUBIC SPLINE

Research article

Voskoboynikov Yu.E.^1, *, Boeva V.A.²

¹ ORCID: 0000-0002-5282-6002;

² ORCID: 0000-0002-5668-3416;

^{1, 2} Novosibirsk State University of Architecture and Civil Engineering, Novosibirsk, Russia;

¹ Novosibirsk State Technical University, Novosibirsk, Russia

* Corresponding author (voscob[at]mail.ru)

Abstract

A universal device for filtering measuring noise is a smoothing cubic spline of defect 1. The magnitude of the filtering error (smoothing) is mostly determined by the value of the smoothing parameter. With the optimal smoothing parameter value, the smoothing error value takes a minimum value. In practice, there is no a priori information on the exact (not noisy) values of the signal, and it is impossible to calculate the value of the optimal smoothing parameter. In this regard, the algorithms used to solve practical problems for choosing the optimal parameter allow for estimating only acceptable smoothing errors, which sometimes significantly exceed the minimum values. The estimation of the optimal smoothing parameter with an unknown variance of the noise measurement of experimental data presents particular difficulty. The current article constructs and examines in detail an algorithm for estimating the optimal parameter based on the L-curve method. This method is used to select the regularization parameter in algorithms for solving incorrectly set tasks. Particular attention is paid to the estimation of the optimal parameter in conditions of correlated noise. Based on the results of these studies, the authors provide practical recommendations for the application of this selection algorithm in the practice of processing experimental data.

Keywords: noise filtering, smoothing cubic spline, smoothing parameter, parameter selection with unknown noise dispersion.

Введение и задача исследования

Сглаживание и дифференцирование зашумленных сигналов (данных) являются наиболее распространёнными задачами при обработке экспериментальных данных [1], часто возникающими в задачах непараметрической идентификации [2], [3]. Следует напомнить, что дифференцирование – это некорректно поставленная задача [4]. Для устойчивого дифференцирования часто используют сглаживающие кубические сплайны (СКС) дефекта единица, которые также эффективны в целях фильтрации содержащихся в обрабатываемых сигналах шумов измерений. На интервале определения сплайна СКС характеризуются непрерывными первыми и вторыми производными. Это позволяет использовать их для вычисления смешанных производных [5], [6]. Основной вопрос, встающий при использовании СКС для решения практических задач, заключается в том, как правильно выбрать параметр сглаживания, величина которого также существенно влияет и на ошибку сглаживания. Следует выбирать некоторое оптимальное значение этого параметра, минимизирующее величину ошибки сглаживания, что невозможно – априорные данные о точных значениях обрабатываемого сигнала отсутствуют. В связи с этим используемые для решения практических задач алгоритмы выбора оптимального параметра позволяют лишь оценить допустимые значения ошибки сглаживания, которые порой в значительной степени превышают минимальные значения. Необходимо рассмотреть два варианта:

1) дисперсия шума измерения задана;

2) данные о дисперсии шума измерения отсутствуют.

Для первого варианта разработаны различные алгоритмы [1], [2] позволяющие оценить оптимальное значение параметра сглаживания с хорошей точностью. Для второго варианта, при неизвестной дисперсии и, в особенности, в случае коррелированного шума, вопрос оценивания параметра сглаживания встаёт остро. Шум с существенной корреляцией между соседними отсчётами может возникать вследствие проведения предварительной обработки зашумлённых исходных сигналов (например, если отфильтровать импульсные шумы нелинейными фильтрами [7]). В работе [7] было показано, что алгоритм оценивания оптимального параметра на основе метода перекрестной проверки (cross-validation method), дает заниженные значения параметра сглаживания, что вызывает значительные ошибки сглаживания.

Все обозначенные выше проблемные вопросы определяют цель данной работы: построение алгоритма оценивания оптимального параметра сглаживания при неизвестной дисперсии шума измерения и коррелированном шуме измерения на основе метода L-кривой и исследование работы этого алгоритма. Попутно ставились следующие задачи:

• построение алгоритма выбора параметра СКС в случае, когда данные о дисперсии шума измерения отсутствуют;
• исследование построенного алгоритма выбора параметра сглаживания при фильтрации коррелированного и некоррелированного шумов измерений.

Сглаживающий кубический сплайн

Для дальнейшего построения алгоритма выбора параметра сглаживания СКС [8], [9] необходимо изложить некоторый теоретический материал о СКС.

Предположим, что на некотором интервале  заданы n узлов , в которых заданы значения функции (сигнала) :

    (1)

где  – случайный шум измерений, характеризуется нулевым средним значением, дисперсия шума задана как . Функция  называется кубическим сплайном дефекта единица, если:

а) функция  является кубическим полиномом вида:

    (2) на каждом отрезке ; б) функция  характеризуется непрерывными первой и второй производной на интервале . Интерполяционный сплайн строится через точки . СКС  строится в окрестности этих точек, величина которой определяется значением параметра сглаживания α. Это дополнительно обеспечивает сглаживание (фильтрацию) шумов измерений. На практике наиболее распространены два вида краевых условий: [1], [8]:

• условия на значения первой производной [1], [8]:

    (3)

• условия на значения второй производной, равные нулю (естественные краевые условия) [1], [8]:

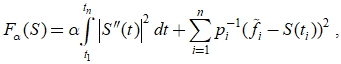   (4) СКС доставляет минимум функционалу [8]:     (5) где – весовые множители i-го измерения  (в случае равноточных измерений задаются одинаковыми, например, ).

Как уже было сказано, ошибка сглаживания в немалой степени зависит от величины параметра сглаживания, и именно параметр сглаживания регулирует гладкость сплайна. В случае малых значений параметра сглаживания фильтрация шумов будет несущественна, следовательно, первая производная примет колебательный вид, что свидетельствует о неустойчивости решения [4]. В случае слишком больших значений параметра сглаживания вторая производная сигнала будет стремиться к нулю, следовательно, сам сплайн будет вырождаться в прямую. Это свидетельствует о «переглаживании» информативных составляющих обрабатываемого сигнала. Оптимальное значение параметра сглаживания, при котором достигается наименьшее значение ошибки сглаживания, находится между двумя этими пределами. На практике априорная информация о точных (не зашумлённых) значениях сигнала отсутствует, и вычислить значение оптимального пара сглаживания невозможно.

Поэтому попытаемся построить оценку для оптимального параметра сглаживания, адаптируя для этой цели метод L-кривой, который иногда используется для выбора параметра регуляризации в алгоритмах решения некорректных задач (например, [10], [11], [12], [13]), при построении регрессионных моделей (например, [14], [15]).

Метод L-кривой и выбор параметра сглаживания кубического сплайна

Первоначально изложим идею метода L-кривой для оценивания параметра регуляризации при решении некорректно поставленных задач [10]. Предположим, дано операторное уравнение I рода вида:

    (6)

для которого нарушаются так называемые условия корректности по Адамару [4], т.е. решение может не существовать, решение может быть не единственным, решение может быть не устойчиво к погрешностям задания правой части f, когда малые погрешности вызывают очень большие ошибки вычисленного решения. Для конкретности в качестве (6) можно рассматривать вырожденную или плохо обусловленную систему линейных алгебраических уравнений, где K – матрица,  – векторы, соответствующих размерностей.

Для нахождения единственного устойчивого решения часто обращаются к методу регуляризации академика А.Н. Тихонова, в котором регуляризированное решение  определяется из условия минимума функционала:

    (7)

где α – параметр регуляризации,  – неточно заданная правая часть (6), D – некоторый оператор, задающий требуемые свойства искомого решения,  – соответствующие нормы. Первое слагаемое (функционал невязки) определяет адекватность решения заданной правой части, второе слагаемое (стабилизирующий функционал) осуществляет отбор (из всех возможных) единственного решения с нужными свойствами. Заметим, что при  получаем неустойчивое (возможно, не единственное) решение метода наименьших квадратов, при  – нулевое решение. Между этими предельными значения параметра регуляризации находится оптимальное значение , при котором ошибка регуляризированного решения

    (8)

  минимальна. Как же оценить  на основе метода L-кривой? Обозначим функционалы, входящие в (7), следующим образом [10]:     (9)

Тогда L-кривой (форма которой напоминает начертание латинской буквы L) называется параметрическая кривая с координатами . В качестве графической интерпретации этого понятия приведем один пример ([10], C. 81-83). В качестве оператора K в (6) была принята прямоугольная матрица размером 410×330 с числом обусловленности 3•10¹⁰. На рисунке 1 в логарифмических масштабах показаны две L-кривые (график 1 – относительный уровень погрешностей задания вектора правой части составляет 3%, график 2 – 15%). На этих L-кривых отчетливо видны два участка: вертикальный и горизонтальный.

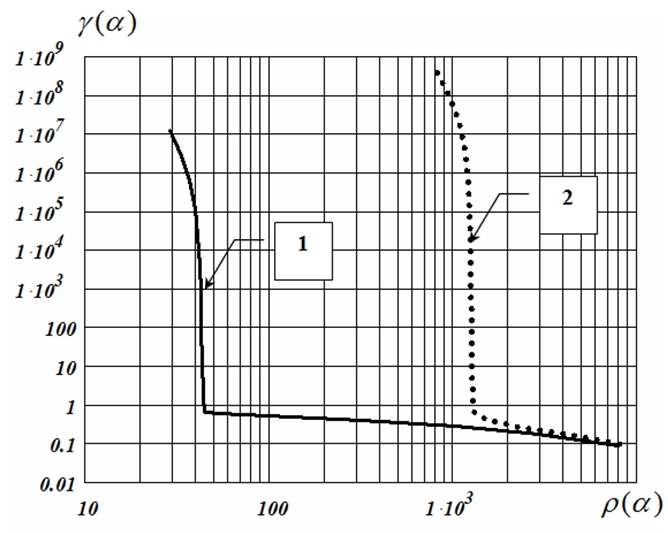
Рис. 1 – Графики L-кривых

 

Наличие вертикального участка (область малых значений параметра регуляризации) обусловлено уменьшением шумовых высокочастотных составляющих в решении , которые практически не «чувствуются» в правой части  и, следовательно, не меняют значение . Горизонтальный участок (область больших значений α) соответствует малым проекциям вектора, что вызывает увеличение . Точка L между двумя этими участками является точкой компромисса: в решении уже отсутствуют шумовые осцилляции, но проекции этого вектора еще не очень «сглажены» и адекватны вектору правой части . Точку L с координатами  называют угловой точкой и определяют из условия максимальной кривизны L-кривой. Вычисление значения параметра регуляризации  в этой угловой точке и составляет суть метода L-кривой.

Можно показать, что кривизна L-кривой определяется следующей формулой:

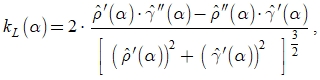    (10) где     (11) В качестве параметра регуляции берется величина , являющаяся решением вариационной задачи:      (12)

В монографии [10] предложен эффективный алгоритм вычисления значения кривизны через коэффициенты дискретного преобразования Фурье. Там же было показано, что алгоритм выбора параметра регуляризации устойчивого алгоритма решения интегрального уравнения I рода изложенным методом позволяет оценить значения  с приемлемой для практике точности (увеличение ошибки регуляризированного решения в среднем не превышало 10-15% по сравнению с ) даже в случае коррелированного шума измерения в выходном сигнале. Этот результат позволяет надеяться на успешное использование метода L-кривой для выбора параметра сглаживания СКС.

Определим функционалы (9) в случае СКС. Сравнивая функционалы (5) и (7), получаем:

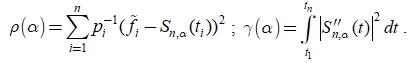   (13)

Если вычисление функционала невязки  по построенному СКС (при заданном параметре α) не вызывает затруднений, то для эффективного вычисления значения стабилизирующего функционала  предлагается следующая формула:

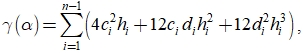   (14)

где   – коэффициенты СКС в представлении (2), вычисленные при заданном параметре α.

Для вычисления значения кривизны по формуле (10) предлагается следующий подход:

1. Исходя из априорной информации задаются два крайних значения параметра сглаживания: минимальное – 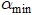; максимальное – 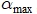, между которыми должно находится оптимальное значение  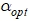(например, ).
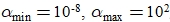2. Между этими крайними значениями формируются узлы 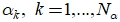, в которых вычисляются значения функционалов  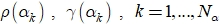(величина  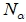выбирается в зависимости от «расстояния» между крайними точками  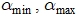из интервала ).
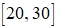3. По значениям 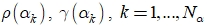, строят два интерполяционных кубических сплайна 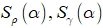, которые затем используются для вычисления первых и вторых производных функционалов 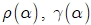, входящих в формулу (10).
4. Используя численные методы одномерной оптимизации, вычисляют точку максимума кривизны 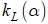(см. (12)).

Результаты вычислительного эксперимента

В целях исследования оптимальных свойств оценок  был выполнен обширный вычислительный эксперимент, некоторые результаты которого приведены в этом разделе. Формировались тестовые сигналы двух видов, с различными спектрами: низкочастотный сигнал 1 (рисунок 2, сплошная кривая) и высокочастотный сигнал 2 (рисунок 2, точечная кривая).

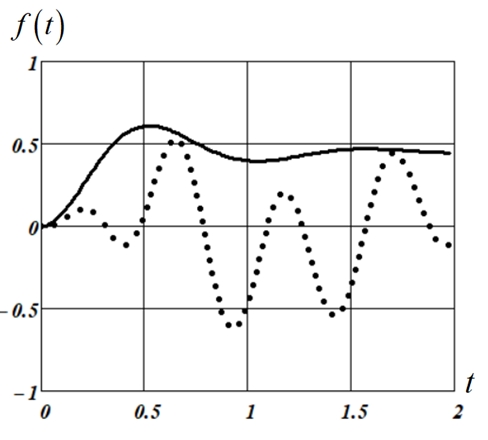
Рис. 2 – Тестовые сигналы

 

Точные значения сигнала вычислялись в узлах , на них накладывался случайный нормально распределенный шум относительного уровня 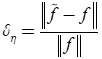, векторы , составлены из значений точной и зашумленной функций в узлах . Относительная ошибка фильтрации определялась выражением 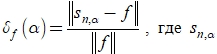 вектор, составленный из значений СКС в узлах сетки. Оптимальный параметр сглаживания  минимизирует ошибку сглаживания  и его можно определить в вычислительном эксперименте, когда известны точные значения обрабатываемой функции – вектор f.

Первоначально рассмотрим случай некоррелированного шума измерения (белый шум). На рисунке 3 показаны зависимости, вычисленные для сигнала 1 при : сплошная кривая – относительная ошибка ; точечная кривая – кривизна (значения меньше 0.001 на рисунке не показаны). Видно, что значения  находятся в области максимума .

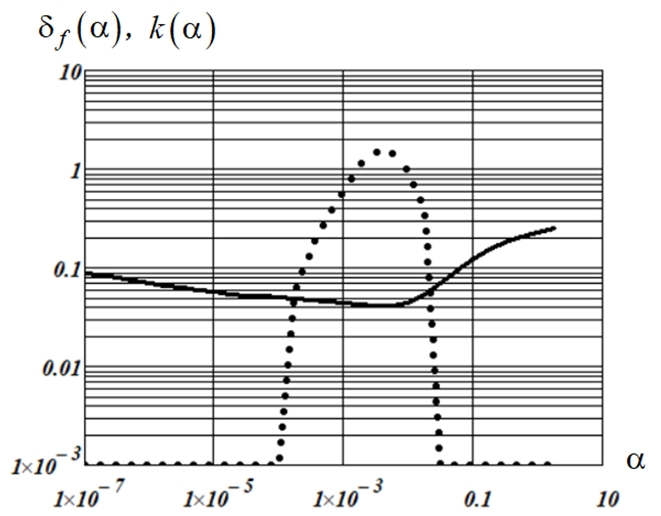
Рис. 3 – Характеристики сглаживания сигнала 1

Примечание: шум не коррелирован

 

На рисунке 4 приведены графики этих зависимостей для коррелированного шума с теоретической корреляционной функцией:  (сильно коррелированный шум).

Видно изменение формы как зависимости , так и зависимости  – они стали более «узкими». Кроме этого, наблюдается небольшое смещение точки  в сторону больших значений параметра сглаживания. По-видимому, такое смещение является следствием коррелированности шума измерения.

В качестве количественной характеристики оптимальности параметра сглаживания  введем коэффициент эффективности :

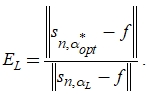    (15)

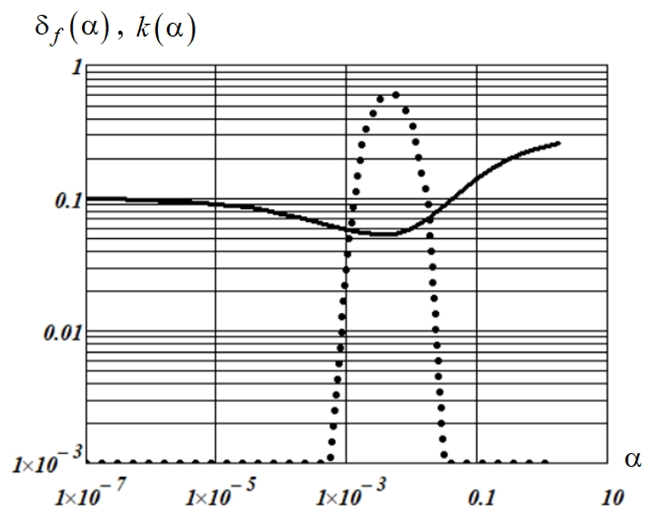
Рис. 4 – Характеристики сглаживания сигнала 1

Примечание: шум коррелирован

 

Чем ближе значения коэффициентов к 1, тем меньше проигрыш по точности параметра сглаживания  по сравнению с . Так как этот коэффициент является случайной величиной со значениями в интервале , то по выборке размером 200 оценивались числовые характеристики: среднее значение  относительной ошибки сглаживания, среднее значение  и минимальное  значение  (которое характеризует максимальный проигрыш по точности в данной выборке). Очевидно, что введенные числовые характеристики позволят количественно, а следовательно, и более объективно отразить свойства параметра . В таблице 1 приведены характеристики для сигнала 1, как для случая не коррелированного, так и для коррелированного шума измерения. В таблице 2 приведены те же характеристики, но для сигнала 2.

 

Таблица 1 – Числовые характеристики сигнала 1

Уровень шума	Шум не коррелирован			Шум коррелирован
0,02	0,009	0,944	0,807	0,017	0,892	0,645
0,05	0,022	0,841	0,594	0,037	0,921	0,450
0,07	0,031	0,783	0,566	0,046	0,946	0,531
0,10	0,036	0,882	0,653	0,063	0,952	0,566
0,15	0,047	0,936	0,697	0,094	0,909	0,508

 

Таблица 2 – Числовые характеристики сигнала 2

Уровень шума	Шум не коррелирован			Шум коррелирован
0,02	0,012	0,941	0,746	0,019	0,970	0,807
0,05	0,026	0,963	0,752	0,046	0,935	0,716
0,07	0,035	0,969	0,769	0,065	0,922	0,695
0,10	0,047	0,976	0,804	0,092	0,906	0,623
0,15	0,067	0,987	0,838	0,136	0,887	0,606

 

Анализ данных этих таблиц позволяет сделать следующие выводы:

1. Для некоррелированного и коррелированного шумов измерений ошибка сглаживания высокочастотного сигнала выше по сравнению с низкочастотным сигналом (сравните столбцы 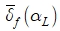 в таблицах 1, 2). Это обусловлено тем, что у высокочастотного сигнала спектры сигнала и шума «перекрываются» в большей степени, чем у низкочастотного сигнала, и это затрудняет разделение составляющих сигнала и шума.
2. При коррелированном шуме измерений ошибка сглаживания возрастает (в 1.5-2 раза) по сравнению с некоррелированным шумом – видно из сравнения столбцов 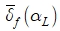 таблиц 1,2. Это обусловлено трансформацией составляющих спектра коррелированного шума в низкочастотную область спектра обрабатываемого сигнала.
3. Во всех рассмотренных случаях (сочетание разных сигналов и шумов) предложенный алгоритм выбора параметра сглаживания позволяет достаточно хорошо оценить оптимальное значение параметра сглаживания. Увеличение ошибки сглаживания при использовании параметра не превышает 5-15% по сравнению с оптимальным параметром сглаживания, вычисление которого на практике невозможно.

Заключение

Как показали проведенные численные эксперименты, предложенный алгоритм оценивания оптимального значения параметра сглаживания на основе метода L-кривой можно рекомендовать использовать на практике для фильтрации некоррелированного и коррелированного шумов измерений. Алгоритм эффективно работает без задания дисперсии или других числовых характеристик шума измерения сигналов, что делает его особенно привлекательным при автоматизированной обработке экспериментальных данных. 

Финансирование Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 20-38-90041.

Funding The reported study was funded by RFBR according to the research project № 20-38-90041.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Воскобойников Ю. Е. Математическая обработка эксперимента в молекулярной газодинамике / Ю. Е. Воскобойников, Н. Г. Преображенский, А. И. Седельников. – Новосибирск : Наука, 1984. – 238 с.
2. Сидоров Д. Н. Методы анализа интегральных динамических моделей: теория и приложения / Д. Н. Сидоров. – Иркутск : Изд-во ИГУ, 2013. – 293 с.
3. Воскобойников Ю. Е. Новый устойчивый алгоритм непараметрической идентификации технических систем / Ю. Е. Воскобойников, В. А. Боева // Современные наукоемкие технологии. – 2019. – №5. – С. 25-29.
4. Тихонов А. Н. Методы решения некорректных задач / А. Н. Тихонов, В. Я. Арсенин. – М.: Наука, 1983. – 284 с.
5. Solodusha S. V. New Classes of Volterra Integral Equations of the First Kind Related to the Modeling of the Wind Turbine Dynamics / S. V. Solodusha // 15th International Conference on Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy's Conference) Moscow, Russia. – 2020. – Р. 35-39. DOI : 10.1109/STAB49150.2020.9140662
6. Воскобойников Ю. Е. Устойчивый алгоритм вычисления смешанных производных в задачах непараметрической идентификации нелинейных систем / Ю.Е. Воскобойников, В.А. Боева // Современные наукоемкие технологии. – 2021. – № 4 – С. 25-29. DOI : 10.17513/snt.38610
7. Воскобойников Ю. Е. Выбор параметра сглаживания кубического сплайна методом перекрестной проверки / Ю. Е. Воскобойников // Norwegian Journal of Development of the International Science. – 2021. – Nо. 66. – Pp. 22-27.
8. Завьялов Ю. С. Методы сплайн-функций / Ю. С. Завьялов, Б. И. Квасов, В. Л. Мирошниченко. – М. : Наука, 1980. – 345 с.
9. Wang Y. Smoothing Splines Methods and Applications. Ser. Monographs on Statistics and Applied Probability v. 121 / Y. Wang. – A Chapman & Hall book. 2011. – 347 p.
10. Воскобойников Ю. Е. Устойчивые алгоритмы решения обратных измерительных задач / Ю. Е. Воскобойников. – Новосибирск : Изд-во НГАСУ (Сибстрин), 2007. – 184 с.
11. Rezghi M. A new variant of L-curve for Tikhonov regularization / M. Rezghi, S. M. Hosseini // J. Comput. Appl. Math., 2012. – No. 231(5). – Рp. 914–924.
12. Cultrera A. A simple algorithm to find the L-curve corner in the regularisation of ill-posed inverse problems / A. Cultrera, L. Callegaro // IOP SciNotes, 2020. – Vol. 1. – Nо. 2. – Рp. 32-39.
13. Ладовский И. В. О методе регуляризации для расчета параметров сглаживающего фильтра при аналитическом продолжении потенциальных полей / И. В. Ладовский, Д.В. Гемайдинов // Уральский геофизический вестник. – 2018. – №3(33). – С. 30-37. DOI : 10.25698/UGV.2018.3.5.30
14. Kerkri A. The L-Curve Criterion as a Model Selection Tool in PLS Regression / A. Kerkri, J. Allal, Z. Zarrouk // Journal of Probability and Statistics, 2019. – Vol. 58. – No. 8. – Pp. 43-54. DOI : doi.org/10.1155/2019/3129769
15. Kerkri A. Highlighting the regularization properties of PLS regression using the conjugate gradient algorithm / A. Kerkri, J. Allal, Z. Zarrouk // International Journal of Applied Mathematics and Statistics, 2017. – Vol. 56. – No. 5. – Pp. 63–74.

Список литературы на английском языке / References in English

1. Voskobojnikov YU. E. Matematicheskaya obrabotka eksperimenta v molekulyarnoj gazodinamike [Mathematical processing of an experiment in molecular gas dynamics] / YU. E. Voskobojnikov, N. G. Preobrazhenskij, A. I. Sedel'nikov. – Novosibirsk : Nauka, 1984. – 238 p. [in Russian]
2. Sidorov D. N. Metody analiza integral'nyh dinamicheskih modelej : teoriya i prilozheniya [Methods for the Analysis of Integral Dynamic Models: Theory and Applications] / D. N. Sidorov. – Irkutsk : Publishing house IGU, 2013.– 293 p. [in Russian]
3. Voskobojnikov YU. E. Novyj ustojchivyj algoritm neparametricheskoj identifikacii tekhnicheskih sistem [New stable algorithm for nonparametric identification of technical systems] / YU. E. Voskobojnikov, V. A. Boeva // Sovremennye naukoemkie tekhnologii [Modern high technologies]. – 2019. – No. 5. – Pp. 25-29. [in Russian]
4. Tihonov A. N. Metody resheniya nekorrektnyh zadach [Methods for solving ill-posed problems] / A. N. Tihonov, V. YA. Arsenin. – M.: Nauka, 1983. – 284 p. [in Russian]
5. Solodusha S. V. New Classes of Volterra Integral Equations of the First Kind Related to the Modeling of the Wind Turbine Dynamics / S. V. Solodusha // 15th International Conference on Stability and Oscillations of Nonlinear Control Systems (Pyatnitskiy's Conference) Moscow, Russia. – 2020. – Р. 35-39. DOI : 10.1109/STAB49150.2020.9140662
6. Voskobojnikov YU. E. Ustojchivyj algoritm vychisleniya smeshannyh proizvodnyh v zadachah neparametricheskoj identifikacii nelinejnyh sistem [Stable algorithm for computing mixed derivatives in problems of nonparametric identification of nonlinear systems] / YU.E. Voskobojnikov, V.A. Boeva // Sovremennye naukoemkie tekhnologii [Modern high technologies]. – 2021. – No. 4 – Pp. 25-29. [in Russian]
7. Voskobojnikov YU. E. Vybor parametra sglazhivaniya kubicheskogo splajna metodom perekrestnoj proverki [Selecting a Cubic Spline Smoothing Option by Cross Validation] / YU. E. Voskobojnikov // Norwegian Journal of Development of the International Science. – 2021. – Nо. 66. – Pp. 22-27. [in Russian]
8. Zav'yalov YU. S. Metody splajn-funkcij [Spline function methods] / YU. S. Zav'yalov, B. I. Kvasov, V. L. Miroshnichenko. – M. : Nauka, 1980. – 345 p. [in Russian]
9. Wang Y. Smoothing Splines Methods and Applications. Ser. Monographs on Statistics and Applied Probability v. 121 / Y. Wang. – A Chapman & Hall book. 2011. – 347 p.
10. Voskobojnikov YU. E. Ustojchivye algoritmy resheniya obratnyh izmeritel'nyh zadach [Stable algorithms for solving inverse measurement problems] / YU. E. Voskobojnikov. – Novosibirsk : Publishing house of NGASU (Sibstrin), 2007. – 184 p. [in Russian]
11. Rezghi M. A new variant of L-curve for Tikhonov regularization / M. Rezghi, S. M. Hosseini // J. Comput. Appl. Math., 2012. – No. 231(5). – Рp. 914–924.
12. Cultrera A. A simple algorithm to find the L-curve corner in the regularisation of ill-posed inverse problems / A. Cultrera, L. Callegaro // IOP SciNotes, 2020. – Vol. 1. – Nо. 2. – Рp. 32-39.
13. Ladovskij I. V. O metode regulyarizacii dlya rascheta parametrov sglazhivayushchego fil'tra pri analiticheskom prodolzhenii potencial'nyh polej [On the regularization method for calculating the parameters of the smoothing filter for the analytic continuation of potential fields] / I. V. Ladovskij, D.V. Gemajdinov // Ural'skij geofizicheskij vestnik [Ural Geophysical Bulletin].– 2018. – No. 3(33). – Pp. 30-37. [in Russian]