ПОВЕРХНОСТИ СВОБОДНОЙ ФОРМЫ В МИКРОТОПОГРАФИИ ПОВЕРХНОСТИ

Косолапов К.В.¹, Обухова Е.А.²

¹Аспирант,²Студент Магнитогорский Государственный Технический Университет

ПОВЕРХНОСТИ СВОБОДНОЙ ФОРМЫ В МИКРОТОПОГРАФИИ ПОВЕРХНОСТИ

Аннотация

Микротопография поверхности играет существенную роль в современных вопросах производства продукта, и затрагивает такие области как машиностроение, металлургия, авиастроение, производство высокоточной оптики и изготовление имплантов. От точного определения характеристик микротопографии поверхности, зависят эксплуатационные свойства изготавливаемых изделий.  Современное производство выдвигает новые требования к регламентации и качеству поверхности, что в свою очередь требует проведения соответствующих исследований. Одной из самых острых задач, является регламентация микротопографии поверхности свободной формы.

Ключевые слова: шероховатость поверхности, свободная форма, вейвлетный анализ.

Kosolapov K.V.¹, Obuhova E.A.²

¹Postgraduate, ²Student, Magnitogorsk State Technical University

FREE-FORM SURFACES IN THE MICRO-SURFACE

Abstract

Microtopography surface plays an important role in the modern problems of production of the product, and covers areas such as mechanical engineering, metallurgy, aviation, manufacturing of precision optics manufacturing implants. The precise definition of the characteristics of the micro-topography surface dependent performance of the manufactured products. Modern production poses new challenges to regulation and quality of the surface, which in turn requires the relevant research. One of the most pressing problems is the regulation of free-form surface microtopography.

Keywords: surface roughness, free form, wavelet analysis.

Целью данной работы было рассмотреть виды и методы представления поверхностей свободной формы, проанализированы способы фильтрации и их результаты, выбрать наиболее подходящие способы фильтрации.

Поверхностями свободной формы называются такие поверхности, которые не имеют осей вращения и трансляционной симметрии и могут иметь любую форму или дизайн.

Поверхности свободной формы могут быть классифицированы на три вида в зависимости от их применения[1]:

Класс 1 : Поверхности, которые включают шаги, ребра и грани. Примером могут служить линзы Френеля, используюемые для коллимации света в маяке и некоторых современных фарах автомобилей.

Класс 2 : Поверхности, имеющие мозаичную картину, то есть повторную структуру по поверхности. Примером может служить 3M Trizac абразивная поверхность, которая состоит из массива треугольной основы микрометра в виде пирамид.

Класс 3 : Гладкие поверхности, такие как, спроектированные без каких-либо шагов, краев или узоров, но опирающиеся исключительно на глобальную геометрию. Примером является телескоп E-ELT, который содержит в конструкции зеркал телескопа сложные сегменты произвольной формы.

Традиционно,  параметризация поверхности проводится с помощью четырех основных шагов, а именно: выборка и представление поверхности , разложение и фильтрация, представление текстуры и наконец  нахождение характеристик и параметров поверхности [1].

Переходя от простых геометрий  к  сложным геометрическим  произвольным формам, многие из традиционных методов, не могут быть универсальны  для выполнения всего спектра задач. Таким образом, требуются новые теории и инструменты, которые могут  решить вновь возникающие вопросы.

Поверхности свободной формы, в отличие от поверхностей с простой геометрией представляют собой не евклидовые объекты[4]. Традиционные методы фильтрации не могут быть применены к данным видам поверхностей, что в свою очередь требует разработки и анализа наиболее подходящих методов фильтрации.

Поверхности свободной формы могут быть представлены двумя основными способами: как облако точек, и как сетка, описывающая данную поверхность. Наиболее подходящим для представления поверхностей свободной формы является метод сеток.

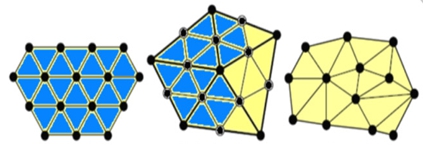
Рис. 1 - Виды сеток для отображения поверхности [1]

 

Существует ряд методов фильтрации поверхности  произвольной формы, представленной в виде сетки [1]:

1. Метод треугольных сеток

Треугольные сетки можно определить как набор вершин (точек), ребер и граней, которые определяют форму или поверхность трехмерного объекта. Можно выделить три основных вида сетки согласно распределению вершин, где  кромки и грани между всей поверхностью: правильные, полуправильные и неправильные сетки.

На рисунке 1 показана правильная сетка.

— это тип сеток, где  вершины правильно распространяются по всей поверхности, все грани имеют почти одинаковую площадь и все вершины имеют одинаковое количество кромок.

– полуправильная сетка.

Это сетка, представляет собой искажённую в некоторых областях поверхности правильную сетку.

– неправильная, случайная сетка.

Сетка, не обладает каким либо из вышеуказанных свойств, площадь каждой грани (треугольника) – отличается от другой, вершины имеют разное количество ребер.

Большинство правильных и полуправильных типов сеток можно найти в компьютерной графике и компьютерной поверхности  объектов, но не очень часто можно найти в фактической измеряемой поверхности. Нерегулярные типы сетки являются более реалистичными и с точки зрения текстуры поверхности больше подходят,  чем два других типа.

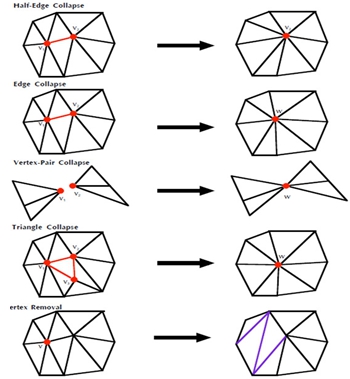
Рис. 2 - Представления способов фильтрации по вершинам сетки [1]

 

Фильтрация поверхности свободной формы представленной методом случайных сеток может быть отфильтрована с помощью ряда операторов[2], таких как :

• Оператор Splite – разбиение на четные и нечетные вершины.
• Оператор Случайный Splite – начальная вершина выбирается случайным образом.
• Оператор Splite с короткими краями – выбирается самый короткий край, затем следующий и так далее по возрастанию, пока не будут обработаны все края.
• QEM(квадратичная ошибка метрик) – помогает сохранить геометрические ошибки аппроксимации треугольных сеток с помощью квадратичной матрицы.
• Оператор упрощения - это процесс уменьшения числа граней, ребер и вершин с сохранением общей геометрии, формы, границ.

Далее были проанализированы реальные и смоделированные поверхности.

Рис. 3 - Поверхности: седло, сфера, холмы, волны [1]

 

Было выбрано четыре компьютерные поверхности, рисунок  3, которые используются для тестирования производительности предлагаемого алгоритма[1]. Эти поверхности охватывают широкий спектр поверхностей произвольной формы с различными типами топологии. Первая поверхность — седло, является типичным примером неевклидовой поверхности с отрицательной кривизной. Вторая поверхность-сфера, представляющая положительную кривизну неевклидовой геометрии. Третья и четвертая поверхности являются более сложными поверхностями с непостоянным искривлением.

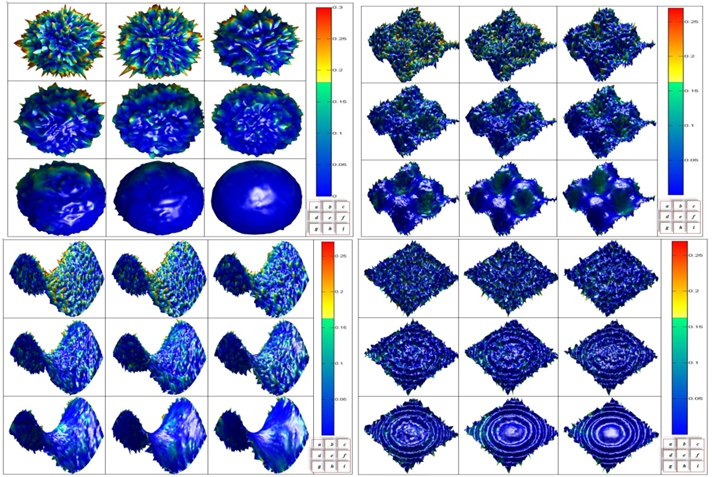
Рис. 4 - фильтрация зашумлённого изображения [1]

 

Далее в эти поверхности был добавлен искусственный шум Гаусса, для последующей,  фильтрации с использованием предложенных методов. [1]

Для фильтрации текстуры поверхности ,использовалась

фильтрация поверхности с помощью вейвлетных  уровней разложения 1,4,8,16,24. Рисунок 4.

Предложенный алгоритм также может применяться для фильтрации других видов поверхности.

Выводы:

В данной работе были рассмотрены виды и методы представления поверхностей свободной формы, проанализированы способы фильтрации и их результаты. Выбраны наиболее подходящие способы фильтрации. Результаты данной работы могут быть использованы для последующей разработки методов фильтрации наиболее подходящих для анализа поверхностей свободной формы.

Литература

1. Abdul-Rahman, Hussein S., Jiang, Xiangqian and Scott, Paul J. “Freeform surface filtering using the lifting wavelet transform”. Издательство Precision Engineering, 37 (1)., 2012, 187-202 с.
2. Jiang, P. Cooper and P. J. Scott. “Freeform surface filtering using the diffusion equation” Proc. Издательство R. Soc. A. 2011 г., 467-505 с.
3. Белов В.К. “Профили поверхности”, издательство “МГТУ им. Г.И. Носова” 2010, 260 с.
4. Мандельброт Б.Б. “Фрактальная геометрия природы”, издательство “Институт компьютерных исследований” 2002 г., 656 с.

References

1. Abdul-Rahman, Hussein S., Jiang, Xiangqian and Scott, Paul J. “Freeform surface filtering using the lifting wavelet transform”. Izdatel'stvo Precision Engineering, 37 (1)., 2012, 187-202 s.
2. X. Jiang, P. Cooper and P. J. Scott. “Freeform surface filtering using the diffusion equation” Proc. Izdatel'stvo R. Soc. A. 2011 g., 467-505 s.
3. Belov V.K. “Profili poverhnosti”, izdatel'stvo “MGTU im. G.I. Nosova” 2010, 260 s.
4. Mandel'brot B.B. “Fraktal'naja geometrija prirody”, izdatel'stvo “Institut komp'juternyh issledovanij” 2002 g., 656 s.