ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ И ПРОБЛЕМЫ ТОЧНОСТИ ПРИ ОБРАБОТКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Карпов В. М.

Доктор технических наук, профессор, ЗАО «НИИИН МНПО «Спектр», Москва, Россия

ПОЛИНОМИАЛЬНАЯ АППРОКСИМАЦИЯ И ПРОБЛЕМЫ ТОЧНОСТИ ПРИ ОБРАБОТКЕ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ

Аннотация

В статье рассматривается возможность перехода от вероятностных оценок к оценкам погрешности. Важность подобного подхода  возрастает с развитием информационных систем для активного контроля в производственных условиях, для систем адаптивного управления, в том числе при работе систем в условиях эксплуатации технически сложных и опасных объектов.

Ключевые слова: регрессия, эмпирические данные, аппроксимация.

Karpov V.M.

Doctor of Technical Sciences, Professor, JSC "RII" Spectrum ", Moscow, Russia

POLYNOMIAL APPROXIMATION AND ACCURACY PROBLEMS IN THE PROCESSING OF EXPERIMENTAL DATA

Abstract

The possibility of a transition from probability estimates to estimates of error. The importance of this approach increases with the development of information systems for the active control in a production environment, adaptive control systems, including the operation of the systems in operation is technically difficult and dangerous objects.

Keywords: regression, empirical data, approximation.

Восстановление регрессии на основе эмпирических данных заставляет решать три основных задачи:

1. Подбор множества аппроксимирующих формул.
2. Оценка параметров регрессионной функции.
3. Оценка близости регрессии к искомой истинной (действительной) функции, т. е. определение точности регрессии.

Для построения моделей часто прибегают к использованию алгебраических полиномов. Методы оценки качества моделей и их параметров базируются на вероятностных характеристиках, например на плотности гауссовского распределения и его параметров. Вместе с тем, оценка близости регрессии к действительной функции может быть реализована только при получении информации о реальном отклонении положения регрессионной функции относительно искомой действительной функции, т. е. необходима информация о погрешности в  C или Lp-метрике, как это решается в задачах классической математики, а не в прикладной статистике. В технических системах особенно остро стоит вопрос о представлении результатов в указанных метриках, поскольку инженеру необходимы данные, характеризующие оценки точности измеряемых величин и только во вторую очередь – получение оценок вероятностных характеристик.

Актуальность перехода от вероятностных оценок к оценкам точностным  возрастает с развитием информационных систем для активного контроля в производственных условиях, для систем адаптивного управления, в том числе при работе систем в условиях эксплуатации объектов энергетических, пожаро и взрывоопасных, когда контролируемые параметры в режиме реального времени достигают границ полей допусков и выходят за их предельные значения. Высокая точность информации в этом случае обеспечивает гарантирование правильного принятия решения автоматизированной системой управления и вероятностные характеристики здесь становятся неуместными или избыточными.

В работе [ 1 ] было показано, что с помощью виртуального компьютерного эксперимента удалось обнаружить, что уравнение регрессии должно содержать систематическую составляющую погрешности даже в том случае, когда в исходных экспериментальных данных она отсутствует. Основным источником систематической составляющей является субъективный некорректный выбор аппроксимирующей функции.

На рисунке 1 условные обозначения переменных представлены следующим образом:

DCm – среднее по диапазону измерения hd значение систематической составляющей погрешности регрессии (приведенная погрешность).

DnCm – приведенная погрешность невязки (определена аналогично).

P1, P2 … - символы, указывающие на степень аппроксимирующего алгебраического многочлена.

Символы  m и max указывают на среднее и наибольшее значение составляющей погрешности в пределах интервала изменения аргумента регрессионной функции.

E – символ, обозначающий емкостный преобразователь перемещения.

V – вектор точечной оценки погрешности рассматриваемого полинома.

На рисунке 1 приведены диаграммы следующих векторов:

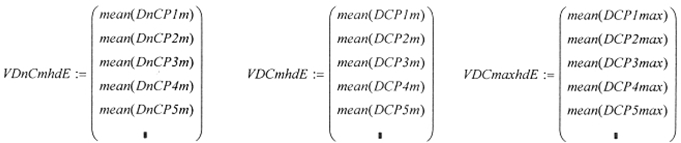
• VDnCmhdE – вектор точечных оценок средних значений невязок для полиномов 2 – 5^й степени.
• VDCmhdE – вектор точечных оценок средних значений систематических составляющих погрешностей для полиномов 2 – 5^й степени.
• VDCmaxhdE – вектор точечных оценок максимальных значений систематических составляющих погрешностей для полиномов 2 – 5-й степени.

Анализ трех векторов для полиномов 2 – 5-й степеней показывает, что вектор невязок (переменная составляющая погрешности регрессии) монотонно уменьшается с возрастанием степени полинома, следовательно, наилучшее решение – это выбор полинома 5-й степени в качестве аппроксимирующей функции. Однако, учитывая наличие систематической составляющей погрешности, весьма значительное преимущество полинома 3-й степени становится очевидным, а значит, выбор аппроксимирующего полинома следует выполнять, только производя анализ систематических составляющих на всем рассматриваемом множестве аппроксимирующих функций.

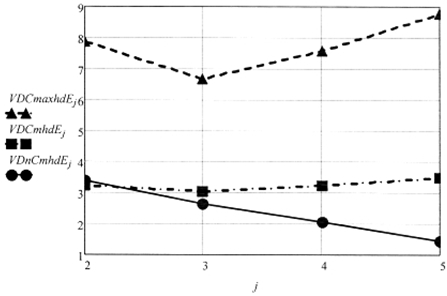
Рис. 1 - Зависимости векторов средних и максимальных значений систематических составляющих погрешности регрессии и средних значений невязки от степени аппроксимирующего полинома

 

Литература

1. Карпов В. М., Анализ эмпирических данных в технической диагностике. 20 Всероссийская научно-техн. конф. по неразрушающему контролю и технической диагностике: тезисы докладов, доклады. Москва, 3-6 марта 2014 г. – М.: Издательский дом «Спектр», 2014 – 512 с. ил.
2. Карпов В.М., ФУНКЦИИ ПРЕОБРАЗОВАНИЯ В МЕТРОЛОГИЧЕСКОМ МОДЕЛИРОВАНИИ. Программные продукты и системы. 2009. № 2. С. 16

References

1. Karpov V. M., Analiz jempiricheskih dannyh v tehnicheskoj diagnostike. 20 Vserossijskaja nauchno-tehn. konf. po nerazrushajushhemu kontrolju i tehnicheskoj diagnostike: tezisy dokladov, doklady. Moskva, 3-6 marta 2014 g. – M.: Izdatel'skij dom «Spektr», 2014 – 512 s. il.
2. Karpov V.M., FUNKCII PREOBRAZOVANIJa V METROLOGIChESKOM MODELIROVANII. Programmnye produkty i sistemy. 2009. № 2. S. 16