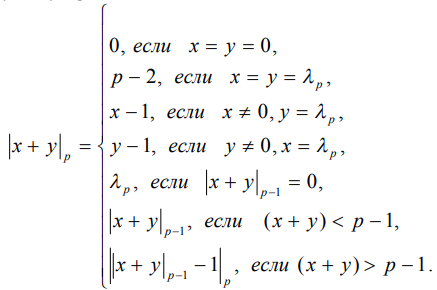THE ARITHMETIC BIMODULAR ARITHMETIC DEVICE OF THE FINAL FIELD GF(P)
Амербаев В.М.1, Балака Е.С. 2
1Доктор технических наук, академик НАН Казахстана, профессор, главный научный сотрудник отдела методологии вычислительных процедур Федерального государственного бюджетного учреждения науки Института проблем проектирования в микроэлектронике Российской академии наук
2Аспирант, Федеральное государственное бюджетное учреждение науки Институт проблем проектирования в микроэлектронике Российской академии наук
АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО БИМОДУЛЬНОЙ АРИФМЕТИКИ КОНЕЧНОГО ПОЛЯ GF(p)
Аннотация
Вводится понятие бимодульной арифметики над полем GF(p). Представлены методы вычисления базовых арифметических операций. Приведены сравнительные оценки характеристик функциональных блоков бимодульной арифметики поля GF(p). Предлагаемые методы используются в аппаратной реализации арифметического устройства бимодульной модулярной арифметики.
Ключевые слова: простое конечное поле Галуа, модульная арифметика, дискретный логарифм.
Amerbaev W. M.1, Balaka E.S.2
1PhD in Technical Sciences, academician of Kazakhstan Academy of Sciences, professor, chief researcher of department of methodology of computing procedures of Institute for Design Problems in Microelectronics of Russian Academy of Sciences
2Postgraduate stuent, Institute for Design Problems in Microelectronics of Russian Academy of Sciences.
THE ARITHMETIC BIMODULAR ARITHMETIC DEVICE OF THE FINAL FIELD GF(P)
Abstract
The concept of bimodular arithmetic over the field GF(p) is entered. Calculation methods of basic arithmetical operations are presented. Comparative estimates of functional block characteristics of bimodular arithmetic of the field GF(p) are given. Offered methods are used in hardware realization of arithmetic device of bimodular RNS.
Keywords: prime finite Galois field, modular arithmetic, discrete logarithm.
Кодирование элементов конечного поля в современной математической литературе можно проводить с использованием: традиционной, логарифметической, бимодульной арифметики конечного поля Галуа GF(p).
Традиционная арифметика опирается на теорему деления Евклида теории чисел, которая позволяет ввести понятие кольца вычетов по модулю m, обозначаемое символом Zm. При простом числе р кольцо вычетов целых чисел  по модулю р обладает свойствами поля, называемое простым полем Галуа и обозначаемое символом GF(p).
по модулю р обладает свойствами поля, называемое простым полем Галуа и обозначаемое символом GF(p).
Для характеризации кольца вычетов по модулю m воспользуемся теоремой деления Евклида, которая утверждает, что справедливо тождество:
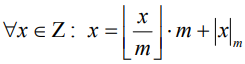 , где
, где 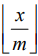 - неполное частное, а
- неполное частное, а 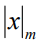 - остаток от деления целого числа x по модулю m. Совокупность всех остатков от деления целых чисел на m обозначают символом
- остаток от деления целого числа x по модулю m. Совокупность всех остатков от деления целых чисел на m обозначают символом 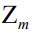 . Заметим, что в теории чисел [1] различаются два рода остатков от деления целых чисел на m – наименьшие неотрицательные и абсолютно наименьшие. Принято также указанные остатки называть вычетами целых чисел по модулю m.
. Заметим, что в теории чисел [1] различаются два рода остатков от деления целых чисел на m – наименьшие неотрицательные и абсолютно наименьшие. Принято также указанные остатки называть вычетами целых чисел по модулю m.
Нетрудно показать, что справедливы следующие тождества:
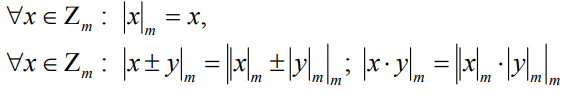 |
Последнее означает, что аддитивные операции кольца 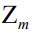 в случае наименьших неотрицательных вычетов реализуются через аддитивные операции целых чисел, согласно следующему выражению:
в случае наименьших неотрицательных вычетов реализуются через аддитивные операции целых чисел, согласно следующему выражению:
|
|
Замечание. Реализация операции вычитания 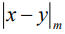 сводится к описанной выше схеме, если заметить, что:
сводится к описанной выше схеме, если заметить, что: 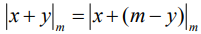 .
.
Модульное умножение выполняется согласно следующему выражению:
|
|
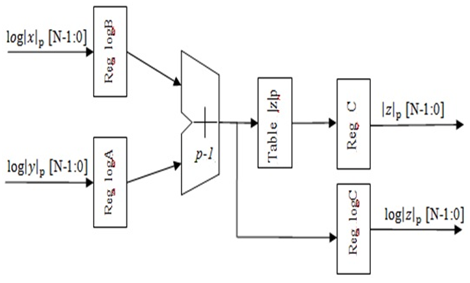
При решении задачи упрощения мультипликативных операций традиционно используется индексная арифметика [5]. Мультипликативная операция реализуется по следующей схеме: если оба элемента ненулевые, то выполняется их преобразование в индексы, что позволяет свести операцию умножения вычетов по модулю р к суммированию индексов операндов по модулю (р-1), а операцию деления – к вычитанию индексов по модулю (р-1). Если же хотя бы один из операндов нулевой, то результат операции умножения нулевой, а операция деления на нуль в поле запрещена. Структурная схема индексного умножителя изображена на рис. 1.
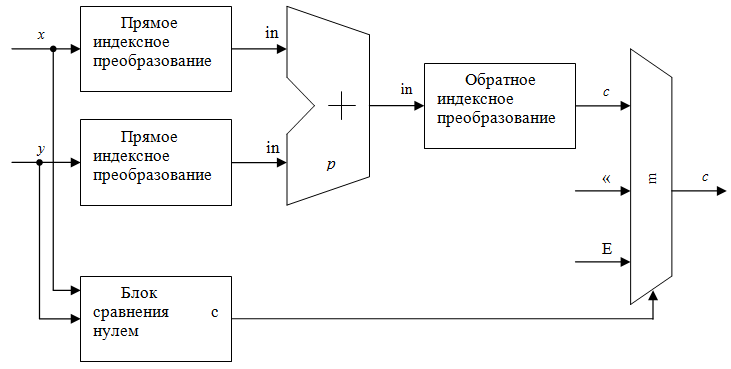
Рисунок.1. Структурная схема индексного умножителя
Сумматор по модулю (p-1) может проектироваться по стандартной схеме модульного суммирования. Однако, наибольший интерес представляют вычисления по модулю (p-1), а именно его разложение на более мелкие множители, т.к. при этом возникает возможность ввести дополнительный параллелизм по каждому каналу, заменив операцию сложения по модулю (p-1) на параллельное сложение по более мелким попарно взаимно простым модулям. Благодаря этому достигается большее быстродействие в сравнении с модулем p.
Другой подход – это отказаться на уровне модульных операций от аддитивных вычислений и перейти к мультипликативным – к логарифметике поля Галуа GF(p).
Логарифмическая система счисления была независимо изобретена и опубликована по крайней мере три раза. Кингсбери и Рейнер представили «логарифмическую арифметику» для цифровой обработки сигналов в 1971 году. Аналогичная LNS была описана в 1975 году Шварцлендером и Алехопоулосом. Ли и Эдгар описал подобную систему счисления, которую они назвали «Фокус», в 1977 году. Математические основы для сложения и вычитания в логарифметике восходят к К.Ф.Гауссу [2], Z.Leonelli, К. Г. Я. Якоби [3].
Суть логарифмического способа состоит в том, что вычисления над GF(p) реализуются как вычисления над элементами поля GF(p), представленными их логарифмами, а логика взаимодействия с нулевыми операндами заменена предикаторами сингулярности. Под сингулярным значением логарифма понимается «значение» логарифма в точке x = 0.
Способ вычислений над полем GF(p) порождается отображением: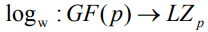 , где
, где 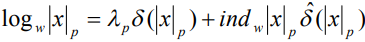 .
.
Здесь |x|p - вычет числа x mod(p); 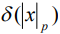 - функция Дирака;
- функция Дирака; 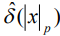 - кофункция Дирака, т.е.
- кофункция Дирака, т.е. 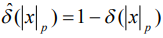 ;
; 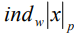 - индекс вычета
- индекс вычета 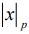 ;
; 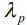 - символ, обозначающий «сингулярное значение» логарифма в точке 0.
- символ, обозначающий «сингулярное значение» логарифма в точке 0.
В данном определении функции Дирака 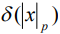 и
и 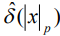 выступают в роли предикаторов сингулярности. Главное требование к символу
выступают в роли предикаторов сингулярности. Главное требование к символу 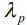 состоит в том, чтобы его двоичное изображение не совпадало ни с каким двоичным изображением элемента поля GF(p). Областью значений дискретного логарифма в отличие от индекса вычета, является множество
состоит в том, чтобы его двоичное изображение не совпадало ни с каким двоичным изображением элемента поля GF(p). Областью значений дискретного логарифма в отличие от индекса вычета, является множество 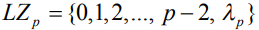 . Характерными точками области определения отображения
. Характерными точками области определения отображения 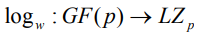 при любом p и любом выборе w являются точки 0, 1, w, p-1; они, соответственно, отображаются в точки:
при любом p и любом выборе w являются точки 0, 1, w, p-1; они, соответственно, отображаются в точки: 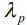 , 0,1,
, 0,1, 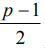 .
.
В соответствие с вышеизложенным, мультипликативные и аддитивные операции представляются в таком виде:
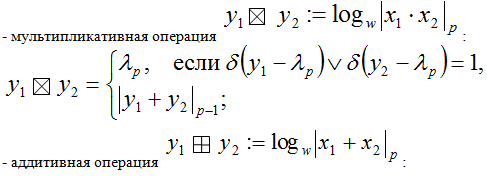
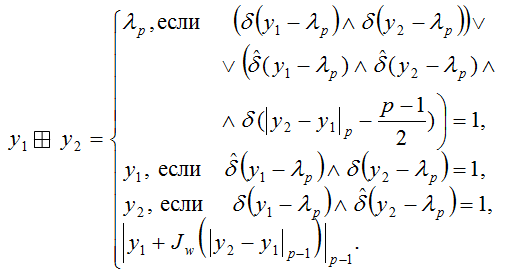
Заметим, что 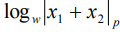 принято называть в честь К.Ф. Гаусса логарифмом Гаусса, а функцию
принято называть в честь К.Ф. Гаусса логарифмом Гаусса, а функцию 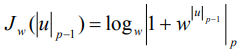 - логарифмом К. Г. Я. Якоби, являющимся частным случаем логарифма Гаусса.
- логарифмом К. Г. Я. Якоби, являющимся частным случаем логарифма Гаусса.
На рисунке 2 представлена структурная схема арифметического устройства логарифметики по модулю:
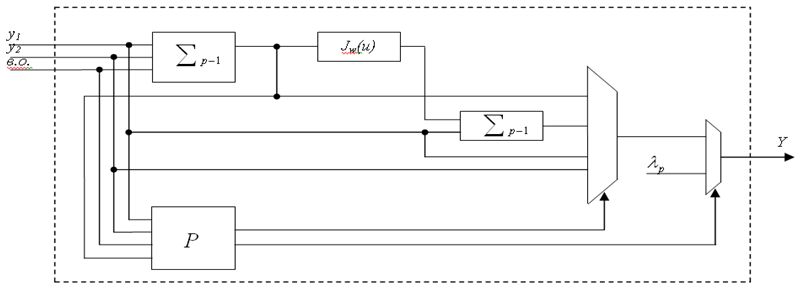
Рисунок. 2. Структура арифметического устройства логарифметики по модулю p
Следующий класс представления вычетов по модулю простого числа предложен проф. Д. А. Поспеловым в работе [6], где рассмотрен прием, суть которого сводится к следующему: вводится представление элементов поля GF(р) посредством пар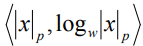 . Достоинством такого подхода является однотипность выполнения аддитивных и мультипликативных операций. Все операции поля выполняются над парами: если требуется найти сумму двух операндов по модулю р, то суммируются по модулю р первые компоненты пар; для формирования второй компоненты пары результата результат суммирования преобразуется в логарифм. Если требуется найти произведение двух операндов по модулю р, то суммируются по модулю (р-1) вторые компоненты пар; для формирования первой компоненты пары результата результат суммирования преобразуется в антилогарифм (вычет). Соответствующую арифметику поля GF(р) назовем бимодульной.
. Достоинством такого подхода является однотипность выполнения аддитивных и мультипликативных операций. Все операции поля выполняются над парами: если требуется найти сумму двух операндов по модулю р, то суммируются по модулю р первые компоненты пар; для формирования второй компоненты пары результата результат суммирования преобразуется в логарифм. Если требуется найти произведение двух операндов по модулю р, то суммируются по модулю (р-1) вторые компоненты пар; для формирования первой компоненты пары результата результат суммирования преобразуется в антилогарифм (вычет). Соответствующую арифметику поля GF(р) назовем бимодульной.
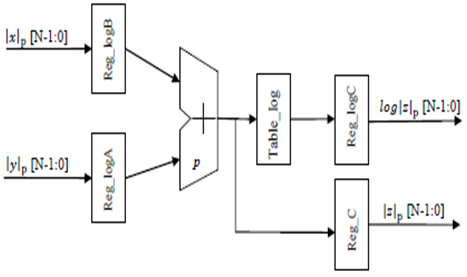
Как было отмечено выше, операции сложения и умножения поля GF(p) сведены к операциям модулярного сложения по модулю р и модулю p-1, соответственно, и одной табличной операции ( рис. 3).
|
Рисунок 3а. Структурная схема операции сложения в бимодульной арифметике |
Рисунок 3б. Структурная схема операции умножения в бимодульной арифметике |
Бимодульная арифметика предполагает структурную однотипность выполнения модульных операций. Для усовершенствования идеи однотипности, в дополнение к структурной однотипности введем кодовую однотипность.
Вычет по модулю р, выраженный через вычет по модулю р-1, представляется в виде:
|
где |
Таким образом, сумматор по модулю p , требующийся для выполнения модульного суммирования, реализуется по следующему выражению:
|
|
На рисунке 4 представлена структурная схема арифметического устройства бимодульной арифметики по модулю:
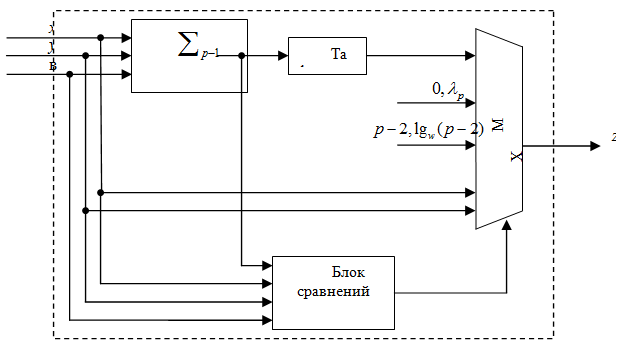
Рисунок. 4. Структура арифметического устройства бимодульной арифметики по модулю p
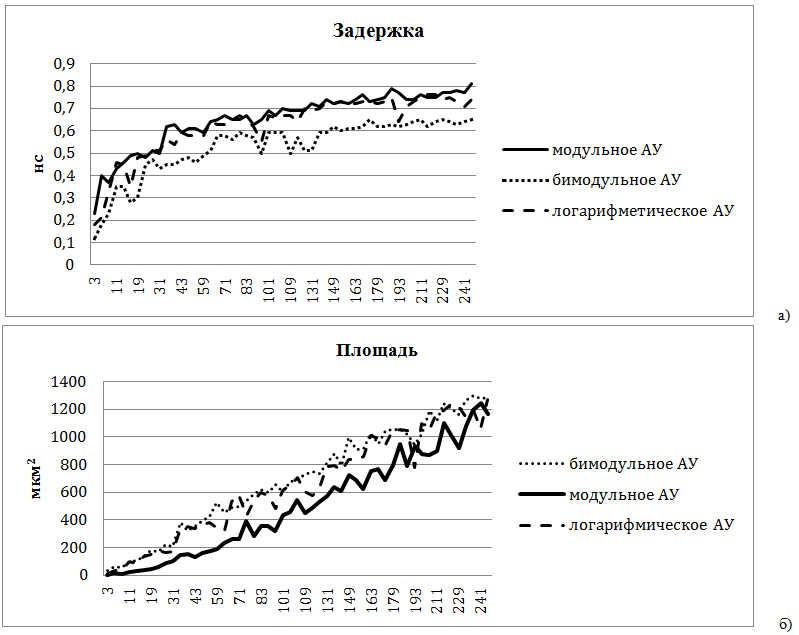
На основе рассмотренных алгоритмов были разработаны RTL-модели типовых устройств вычисления базовых операций бимодульной арифметики с использованием стандартных алгоритмов построения модульных сумматоров и алгоритмов субмодулярного построения сумматоров. На языке Perl созданы автоматизированные генераторы функциональных представлений для создания высокоуровневого Verilog описания соответствующих блоков. На рис.5 представлены результаты сравнительного анализа эффективности аппаратной реализации базовых операций бимодульной арифметики. Анализ проводился путем сравнения временных характеристик блоков, полученных в результате структурного синтеза и статического временного анализа. Для эксперимента были выбраны простые числа в диапазоне 8 бит, используемые в качестве модулей. Структурный синтез проводился средствами САПР Synopsys Design Compiler с применением свободно распространяемой библиотеки стандартных ячеек NangateOpenCellLibrary с нормами проектирования 45 нм.
|
Рисунок 5. Аппаратные(а) и временные(б) затраты на реализацию арифметического устройства по модулю р |
Как показывают результаты синтеза, применение аппарата бимодульной арифметики для построения арифметического устройства, имеющих практически во всех случаях меньшее время задержки при незначительном увеличении аппаратных затрат, является более эффективным решением по сравнению со стандартным методом проектирования.
Бимодульная арифметика сочетает в себе преимущества традиционной модульной и логарифмической арифметик. Вычисления в ней предоставляют большую свободу в выборе проектных решений в рамках двоичных технологий для проблем повышения быстродействия, сокращения аппаратных затрат и проблем организации надежных вычислений.
References
И.М. Виноградов Основы теории чисел, изд. 8- М: “Наука”, 1972. 167 c.
Математический Энциклопедический словарь. М.: Сов. Энциклопедия,1988. С. 141,330.
Р. Лидл, Г. Нидеррайтер Конечные поля: в 2 т. / под общ.ред. В.И. Нечаева. М.: Мир, 1988.
Амербаев В. М., Балака Е. С., Константинов А. В., Тельпухов Д. В., «Методы ускорения вычислений скалярных произведений векторов в базисе модулярной логарифметики», IV Всероссийская научно-техническая конференция «Проблемы разработки перспективных микро- и наноэлектронных систем – 2010»: сб. научн. тр. / под общ. ред. А.Л. Стемпковского”. - М.: ИППМ РАН, 2010. - С. 378 – 381.
A.P. Preethy and D. Radhakrishnan An RNS based logarithmic adder, IEE Proceedings - Computers and Digital Techniques, Vol. 147, Issue 4, July 2000.
Д.А. Поспелов Арифметические основы вычислительных машин дискретного действия. М.: Высш. шк., 1970.

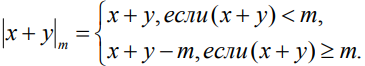
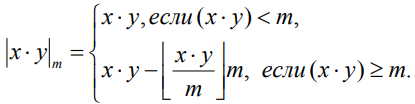
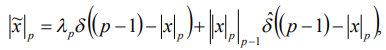
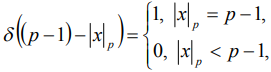 - функция Кронекера,
- функция Кронекера, 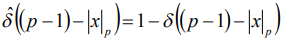 -кофункция Кронекера.
-кофункция Кронекера.