РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ПРОЦЕССА РОСТА НИТЕВИДНЫХ КРИСТАЛЛОВ

Косырева Л. Г.¹, Чернышов А. Д.², Козенков О. Д.³

¹Аспирант; ² доктор физико-математических наук, профессор, Воронежский государственный университет инженерных технологий; ³ кандидат физико-математических наук, доцент, Воронежский государственный технический университет.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ ПРОЦЕССА РОСТА НИТЕВИДНЫХ КРИСТАЛЛОВ

Аннотация

В ходе моделирования процесса роста нитевидных кристаллов по механизму пар-жидкость-кристалл получена зависимость скорости роста от радиуса кристалла. Получено качественное схождение рассчитанных зависимости с экспериментальными данными.

Ключевые слова: нитевидный кристалл, механизм пар-жидкость-кристалл, модель роста.

 

Kosyreva L.G.¹, Chernyshov A.D.², Kozenkov O.D.³

¹ Postgraduate student; ² professor, doctor of physical and mathematical sciences, Voronezh state university of engineering technologies; ³ associate professor, candidate of physical and mathematical sciences, Voronezh state technical university.

RESULTS OF MODELLING OF PROCESS GROWTH OF WHISKERS

Abstract

During modeling of process of how whiskers growth for the vapor-liquid-crystal mechanism we received dependence of growth rate on crystal radius. The qualitative convergence calculated dependences with experimental data is received.

Keywords: whiskers, vapor-liquid-crystal mechanism, model of growth.

Нитевидные кристаллы ("усы", виcкерсы), монокристаллы в виде игл или волокон. Размеры нитевидных кристаллов в одном направлении во много раз больше, чем в остальных: типичная длина от 0,5 мм до нескольких мм, диаметр 0,5-50 мкм. Нитевидные кристаллы характеризуются высокой однородностью и совершенством структуры. В очень тонких (диаметр < 1 мкм) нитевидных кристаллах, как правило, нет дислокаций [1].

Рост нитевидных кристаллов (НК) по механизму пар-жидкость-кристалл (ПЖК) исследовался многими учеными и не изучен до конца по настоящее время. Не смотря на то что разработано большое число кинетических моделей роста, представления о механизме роста остаются нераскрытыми до конца.

В настоящей работе предпринята попытка более глубокого изучения процессов роста по механизму пар-жидкость-кристалл. Предположено, что подвод вещества к границе роста НК (рис. 1), описывается законом нестационарного массопереноса [2].

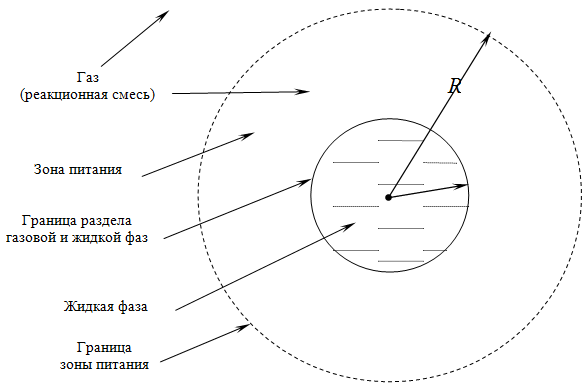
Рис. 1 – Схема модели

В сферических координатах этот закон записывается следующим образом:

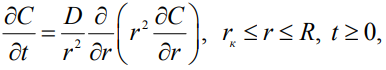(1)

где C – концентрация химического соединения, содержащего кристаллизующееся вещество, в зоне питания; 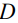 – коэффициент диффузии, который для упрощения задачи будем считать постоянным (2·10^-4 м²/с), 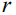– радиус материальной точки кристалла, 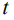– время,  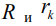– внешний и внутренний радиусы «зоны питания». Радиус жидкой капли принимается равным радиусу кристалла  .

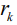Концентрацию компонента содержащего кристаллизующееся вещество в начальный момент времени на границе зоны питания кристалла считаем постоянной

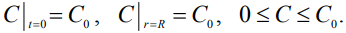(2)

На границе раздела жидкой и газообразной фаз граничное условие запишем в виде условия третьего рода (условие Смолуховского)[3]

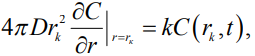(3)

где 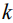  – константа скорости прямой химической реакции .

Для решения задачи (1)-(3) используем метод быстрых разложений, предложенный в работах [4-5]. Полное решение данной задачи описано в статье [6].

Полученные, в ходе решения, данные позволили построить зависимость скорости роста от радиуса кристалла (рис. 2). Скорость роста рассчитана по формуле [6]:

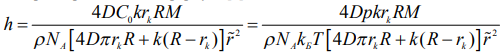(4)

где 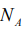 - число Авогадро (6,02214129·10²³ моль^-1),  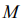- молярная масса кремния (28,0855 г/моль),  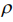- плотность кремния (2,33 г/см³). Отношение площадей возьмем равным 4, k – константа скорости химической реакции (от 1 до 0,001 м³/с),  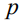 - давление (10^-3 Па),  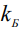- константа Больцмана (1,3806488·10^-23 Дж/К),  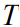 - температура (1350 К).

В работе авторов [1] есть экспериментальная зависимость скорости роста от радиуса кристалла, представленная на рис. 2 жирными точками.

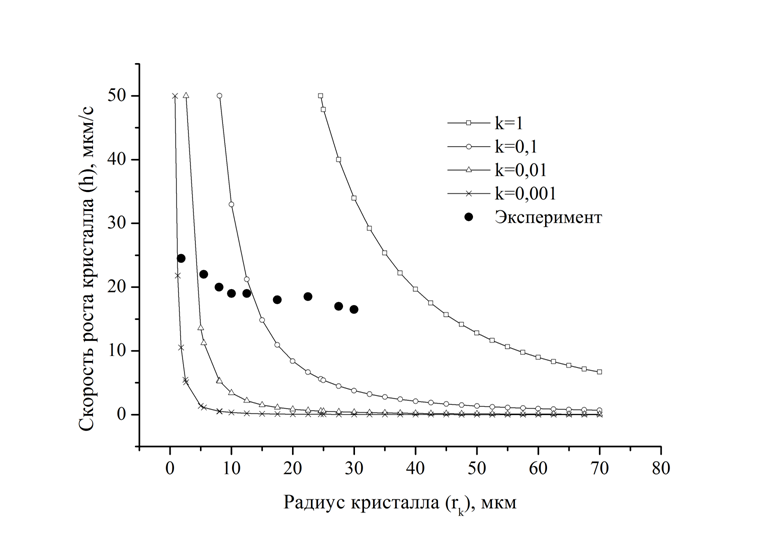
Рис. 2 – Зависимость скорости роста от радиуса кристалла

Анализ полученных зависимостей показал, что характер изменения скорости роста качественно соответствует экспериментальным данным. Эксперименты показывают, что рост нитевидных кристаллов наблюдается в определенных интервалах температуры, давления и др. Графики, представленные на рис. 2, получены при средних значениях из этих интервалов. Однако, для полного соответствия необходимо правильно выбрать соотношение исходных параметров, таких как: температура, давление, коэффициент диффузии, отношение площадей.