РЕГУЛИРОВАНИЕ УСИЛИЙ ПРИ ПОДБОРЕ ПАРАМЕТРОВ L, EI И C ЧЕТЫРЕХПРОЛЕТНОЙ СИММЕТРИЧНОЙ БАЛКИ НА УПРУГИХ ОПОРАХ

Овсянников М.Ю.¹, Кузнецова С.Г.²

¹Студент 4 курса; ²кандидат технических наук, доцент, Пермский национальный исследовательский политехнический университет

РЕГУЛИРОВАНИЕ УСИЛИЙ ПРИ ПОДБОРЕ ПАРАМЕТРОВ L, EI И C ЧЕТЫРЕХПРОЛЕТНОЙ СИММЕТРИЧНОЙ БАЛКИ НА УПРУГИХ ОПОРАХ

Аннотация

При проектировании симметричной четырехпролетной балки постоянной жесткости EI, при одинаковых пролетах l и на упругих опорах, находящейся под действием равномерно распределенной нагрузки, опорные моменты равны. Регулируя эти усилия балки, подобраны параметры: величина пролета l, жесткость при изгибе EI и упругая характеристика c. Примером конструкций, для которых балка на упругих опорах является расчетной схемой, может быть, например, фундаментная или подкрановая балка.

Ключевые слова: неразрезная регулярная балка, метод сил, уравнение пяти моментов, упруго оседающие опоры, вертикальное смещение опоры.

Ovsyannikov MY¹, Kuznetsova SG²

¹4rd year student; ²PhD in technics, associate professor, Perm National Research Polytechnic University.

REGULATION OF EFFORTS FOR SELECTION OF PARAMETERS L, EI AND C OF SYMMETRIC FOUR-SPAN BEAM ON ELASTIC BEARINGS

Abstract

In the design of a symmetrical four-span continuous beam with stiffness constant, equal spans on elastic bearings under a uniformly distributed load, bending moments on bearings are equal. Adjusting these efforts, selected parameters: the span l, stiffness EI and the elastic characteristics c. The example of this structure may be the foundation or the crane beam.

Keywords: continuous regular beam, area - moment method, equation of the five moments, elastic bearings, vertical offset of bearing.

Запроектируем симметричную регулярную четырехпролетную балку на упругих опорах (т.е. определим параметры l, EI, c), в которой под действием равномерно распределенной нагрузки изгибающие моменты на опорах равны (рис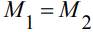. 1):

                                                                                                  (1)

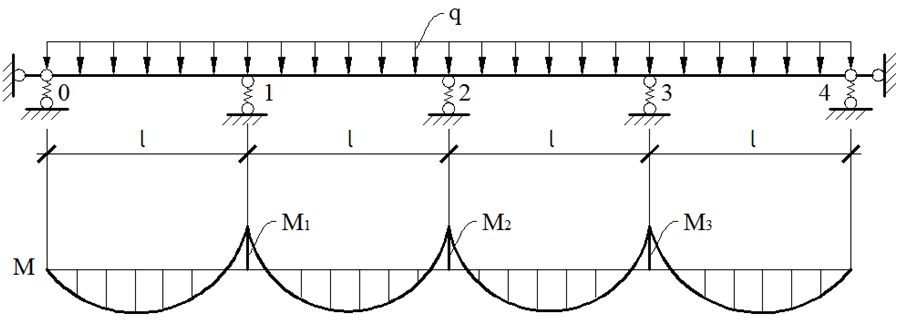
Рис. 1. Неразрезная четырехпролетная балка

Используем метод сил для проектирования балки на упругих опорах [1]. Основной системой метода сил будет являться балка с врезными шарнирами над опорами (рис. 2).

Рис. 2. Основная система метода сил

Так как балка и нагрузка симметричная, моменты, возникающие в балке над первой и третьей опорами, равны:

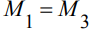                                                                                                  (2)

Составим уравнение пяти моментов относительно первой опоры используя симметрию балки (2) [2]:

    

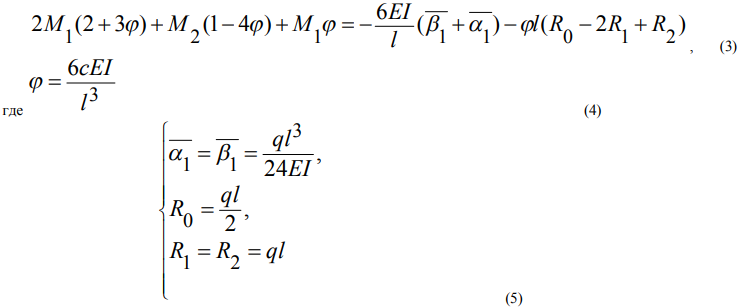
Подставим найденные значения (5) в уравнение (3):                                                                                                          

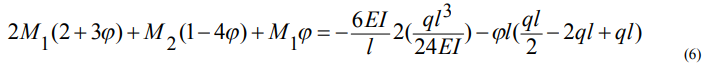
Преобразовав уравнение (6), получим:

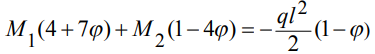                                      (7)

Аналогично, уравнение пяти моментов относительно второй опоры: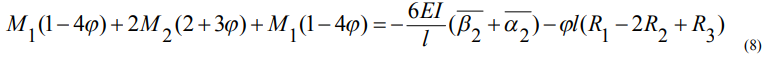      

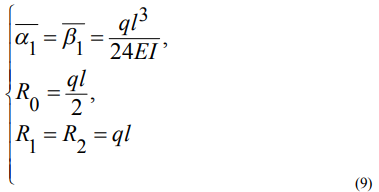
Подставив значения (9) в уравнение (8) и преобразовав его, получаем:

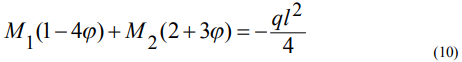
Решим систему из уравнений (7) и (10) методом определителей.

Вычислим определители системы:

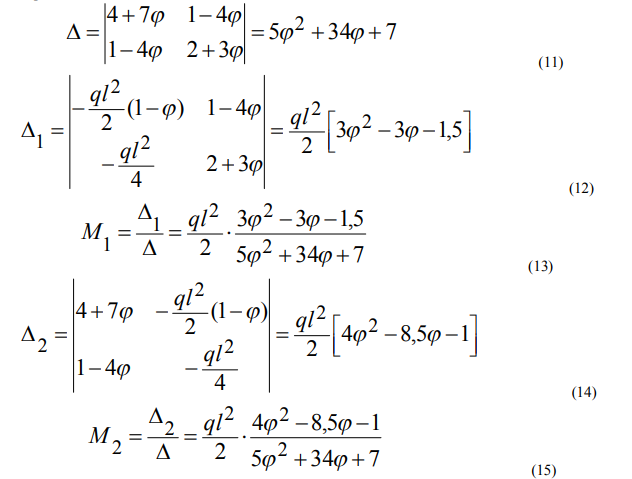
Приравняем полученные моменты по условию (1), сократив одинаковые множители:

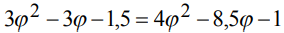                                                                    (16)

Из уравнения (16) получаем следующее квадратное уравнение:

                                             

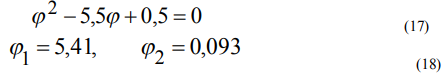
Исходя из уравнения (4) и зная значение φ, мы можем запроектировать балку с необходимыми параметрами.

Значения опорных моментов:                                           

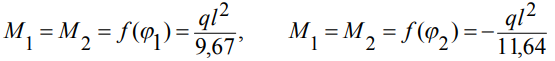                          (19)

По найденным значениям 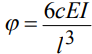 можно утверждать, что существует 2 варианта искомых балок, параметры которых соответствуют значениям  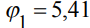и .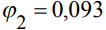

Балка постоянной жесткости и с одинаковыми пролетами с 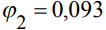 приближается к балке на жестких опорах, т.к. 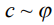, а балка с  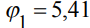- к балке на податливых опорах. Это утверждение необходимо учитывать при проектировании четырехпролетной симметричной балки на упругих опорах.