RATIONAL FORM OF GEOMETRIC NONLINEAR SHALLOW SHELLS ON THE ROUND PLAN FORM AT DIFFERENT TYPES OF LOADING INVESTIGATION
Ступишин Л.Ю.¹, Колесников А.Г.², Озерова Т.А3
¹Кандидат технических наук, профессор, заведующий кафедрой городского, дорожного строительства и строительной механики; ²Кандидат технических наук, доцент кафедры городского, дорожного строительства и строительной механики; 3Магистрант кафедры городского, дорожного строительства и строительной механики. «Юго-Западный государственный университет»
МЕТОДИКА ОПРЕДЕЛЕНИЯ РАЦИОНАЛЬНОЙ ФОРМЫ ПОЛОГИХ ГЕОМЕТРИЧЕСКИ НЕЛИНЕЙНЫХ ОБОЛОЧЕК НА КРУГЛОМ ПЛАНЕ ПРИ РАЗЛИЧНЫХ ВИДАХ НАГРУЖЕНИЯ
Аннотация
В статье рассмотрена методика определения рациональной формы пологих оболочек на круглом плане при различных видах нагружения и способах опирания. Методика позволяет обеспечить ресурсо- и энергоэффективность оболочечных конструкций, увеличить их эксплуатационную надежность, а так же более точно учитывать расчетные параметры нагружения в проектировании, находить рациональные проекты оболочек при различных видах нагружения и опирания.
Ключевые слова: напряженно-деформированное состояние, пологие геометрически нелинейные оболочки, оболочки переменной формы, различные виды нагружения, способы опирания.
Stupishin L.Yu¹, Kolesnikov A.G.², Ozerova T.A3.
1Candidate of Sciences, Professor, Head of the Urban and Road Construction and Structural Mechanics Chair, Southwest State University.
2Candidate of Sciences, Docent of the Urban and Road Construction and Structural Mechanics Chair, Southwest State University.
3 Student of the Urban and Road Construction and Structural Mechanics Chair, Southwest State University.
RATIONAL FORM OF GEOMETRIC NONLINEAR SHALLOW SHELLS ON THE ROUND PLAN FORM AT DIFFERENT TYPES OF LOADING INVESTIGATION
Abstract
Rational geometric nonlinear shallow shells on the round plan are investigated for type of fixing and types of loading.
Keywords: shallow shells, nonlinearity, critical force, pressure, variable form.
Изменение напряженно – деформированного состояния пологих геометрически нелинейных оболочек переменной формы срединной поверхности в зависимости от вида нагружения и типа опирания остается мало исследованным. Предлагаемая методика определения критической нагрузки и напряжений в геометрически нелинейной пологой оболочке переменной формы позволяет более точно учесть расчётные параметры нагружения в реальном проектировании, находить рациональные проекты оболочек при различных видах нагружения и опирания краев.
Форма оболочки вращения переменной формы описывается уравнением ее меридиана. В качестве такой образующей принята параболическая кривая [1]:
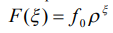 , (1)
, (1)
где 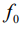 - стрела подъема оболочки;
- стрела подъема оболочки;
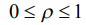 - безразмерный радиус основания оболочки;
- безразмерный радиус основания оболочки;
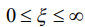 - параметр формы срединной поверхности оболочки.
- параметр формы срединной поверхности оболочки.
Методика определения значений величин критических нагрузок и напряжений для различных видов закрепления краев оболочек приводится в работах [1, 2]. Решались задачи определения критической нагрузки и напряжений в металлических оболочках с переменной формой срединной поверхности для наиболее распространенных в практике проектирования типов опирания и видов нагружения (рисунок 1). Результаты сравнивались с уже известными работами [3].
Рассмотрим графики зависимости (рисунок 2) параметра критической нагрузки от параметра формы ξ при действии различных вертикальных нагрузок (рисунок 1): сосредоточенной, круговой и кольцевой. Условия опирания: 1 – жесткое защемление; 2 – скользящая заделка; 3 - шарнирно-подвижное опирание. Материал оболочки считается линейно упругим.
а)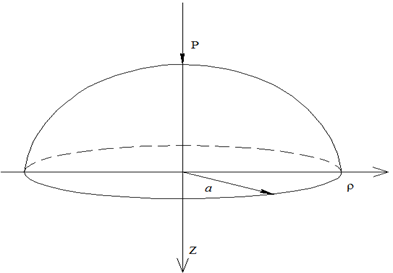 б)
б)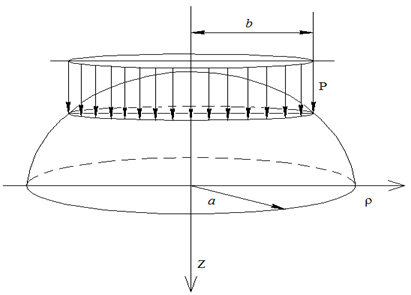
в)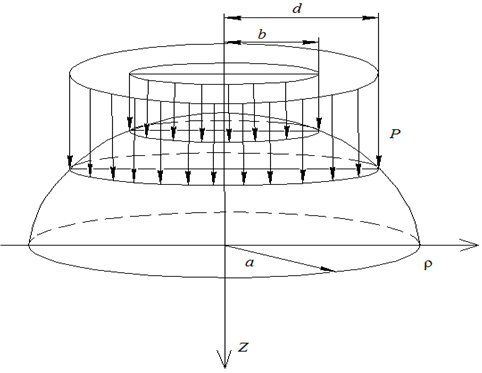
Рисунок 1 – Расчетная схема пологой оболочки при действии: а) сосредоточенной нагрузки, б) нагрузки равномерно распределенной по окружности радиусом b, в) нагрузки равномерно распределенной по кольцу, с внешним радиусом - d и внутренним – b
а)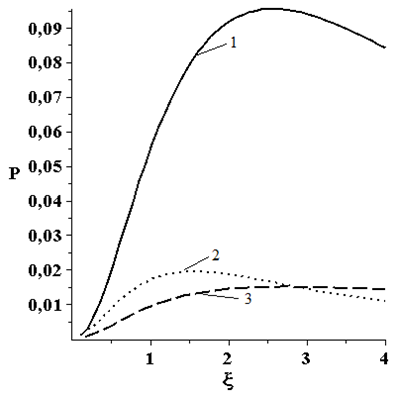 б)
б)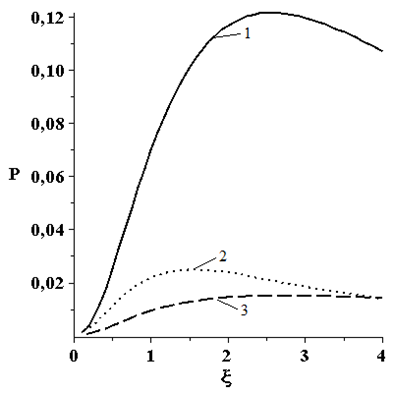
в)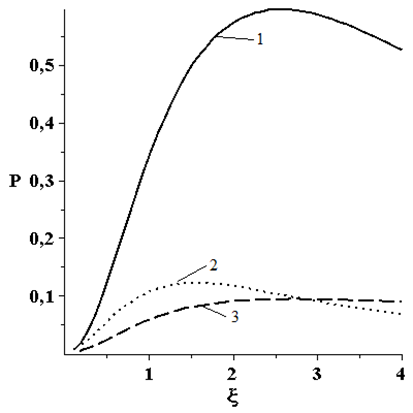 г)
г)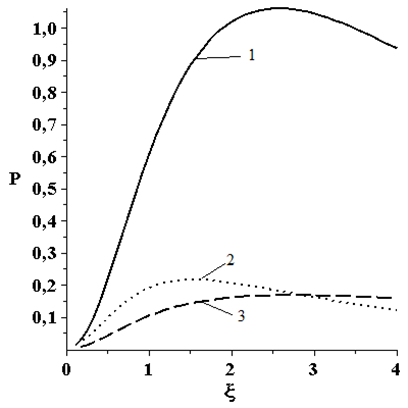
Рисунок 2 – График зависимости параметра критической нагрузки от параметра формы ξ при: а) равномерно распределенной нагрузке; б) сосредоточенной нагрузке, в) нагрузке равномерно распределенной по окружности радиусом b, г) нагрузке равномерно распределенной по кольцу, с внешним радиусом - d и внутренним – b
(значения параметра критической нагрузки даны в безразмерных величинах)
Из графиков следует вывод о том, что при параметре формы ξ=2,5, ξ=1,5 и ξ=2,7, для жесткого защемления, скользящей заделки и шарнирно-подвижного опирания соответственно, оболочка воспринимает максимальную критическую нагрузку.
Использование данной методики дает возможность определять рациональные формы пологих оболочек на круглом плане при различных видах нагружения и способах опирания, что способствует ресурсо- и энергоэффективности оболочечных конструкций, а также позволяет увеличить их эксплуатационную надежность.
References
Ступишин Л.Ю. Приближенный способ определения оптимальной формы пологих геометрически нелинейных оболочек вращения при условии устойчивости [Текст]: Л.Ю. Ступишин // Известия высших учебных заведений. Строительство и архитектура.- 1989.- №9.- С. 28-32
Ступишин Л.Ю. Приближенный способ определения оптимальной формы пологих оболочек на прямоугольном плане [Текст]: Л.Ю. Ступишин // Известия высших учебных заведений. Строительство и архитектура.- 1991.- №4.- С. 37-40
Ступишин Л.Ю. Исследование напряженно-деформированного состояния пологих геометрически нелинейных оболочек на круглом плане переменной формы при различных видах нагружения. [Текст]: Л.Ю. Ступишин, А.Г. Колесников, Озерова Т.А. // Промышленное и гражданское строительство: ежемесячный научно-технический и производственный журнал, 2013 г.-№5.- С.11-12
