РАСЧЕТ ПОНДЕРОМОТОРНЫХ ФАКТОРОВ ПРИ ЭЛЕКТРОПЛАСТИЧНОСТИ МОНОКРИСТАЛЛА СУРЬМЫ

Прокопович Е.В.¹, Капора С.В.², Савенко В.С.³

^1,2Магистрант; ³доктор технических наук, профессор,  МГПУ им. И. П. Шамякина,

РАСЧЕТ ПОНДЕРОМОТОРНЫХ ФАКТОРОВ ПРИ ЭЛЕКТРОПЛАСТИЧНОСТИ МОНОКРИСТАЛЛА СУРЬМЫ

Аннотация

В статье произведены расчёты собственного магнитного поля тока образца сурьмы.

Ключевые слова: электропластическая деформация, пинч-эффект, собственное магнитное поле.

Prokopovych E.V.¹, Kapora S.V.², Savenko V.S.³

^1,2 MA student; ³Doctor of Technical Sciences, Professor, Chief of Physics Department Mozyr State Pedagogical University Name I.P. Shamyakin,.

CALCULATION OF FACTORS IN PONDEROMOTIVE ELEKTROPLASTICHNOSTI MONOCRYSTAL SB.

Abstract

In this paper the calculations of the intrinsic magnetic field of the current sample of antimony.

Keywords: Electroplastic strain, pinch effect, its own magnetic field.

Импульс электрического тока (1,5 10³ А/м²) пропущенный через кристалл во время деформации вызывает вторичные пинч- и скин-эффекты, а также термическое разупрочнение решетки. Оценим вклад этих факторов в явление электропластичности при двойниковании кристаллов сурьмы. [1]

На поверхности образца собственное магнитное поле тока принимает максимальное значение 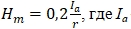– амплитудное значение силы тока в проводнике. 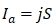, где S – площадь поперечного сечения проводника.

На образца Sb при плотности тока j = 1,5 × 10³А/мм² и радиусе сечения проводника r = 2 мм, собственное магнитное поле тока, возникающее на поверхности проводника.

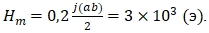
При r = 5 мм максимальном значении 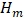 принимает значение

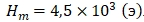
Таким образом, можно сделать вывод, что чем больше радиус образца, тем соответственно больше пинч-эффект.

Рассмотрим механическое давление на поверхности образца. Оно составляет: 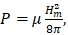 где Р – механическое давление (Па), μ – магнитная постоянная равная 1,257 × 10^-6 Н/А².

 

Из последнего выражения следует, что при одной и той же плотности тока, например j = 1,5 × 10³А/мм², пондеромоторное действие будет выражено тем больше, чем больше радиус использованного образца.

Пинч-эффект является масштабным фактором и квадратично зависит от r и j. Для образцов малого радиуса он не должен наблюдаться.

Максимальная осевая сила F_z от пинч-эффекта равна 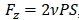, где F_z – максимальная осевая сила, ν – коэффициент Пуассона равный 0,27, Р – механическое давление, S – площадь сечения образца.

Тогда, для образца с r = 2 мм и Р = 0,45 Па. 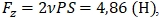, для образца с r = 5 мм и Р = 1,013 Па. .

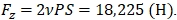Пинч-эффект тем больше, чем больше осевая сила образца.

Материал образца, также играет особую роль, чем меньше проводимость металла, тем больше скорость диффузии магнитного поля в образце, и соответственно пинч-эффект меньше.

Также величина пинч-эффекта зависит от круговой частоты: 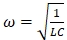 , где ω – круговая частота (Гц), L – индуктивность равная 10^-7 (Гн), С – ёмкость равная 10^-3(Ф). Получаем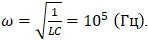

Чем больше частота ω, тем более ярко выражен пинч-эффект. Для того чтобы иметь высокие значения импульса тока необходимо использовать конденсаторы большей ёмкости С, при этом увеличения частоты  приводит к уменьшению индуктивности цепи L.

Добротность контура Q, определяемая выражением 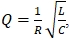, где R – полное активное сопротивление цепи (Ом).

Добротность контура должна быть небольшой, например при 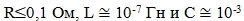 Ф составлять величину Q ≤ 0,1. [2]

Длительность импульса должна быть минимальна

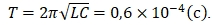
Рассчитаем толщину скин-слоя для образца

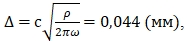
где Δ – толщина скин-слоя, с – электродинамическая постоянная равная 3 × 10¹⁰ см/с, ρ – удельное электросопротивление, для сурьмы равно 43,045 × 10^-6 Ом × см.

Для достижения максимума пинч-эффекта необходимо выбирать такую частоту импульсов тока, при которой магнитное поле не успевает существенно проникать через поверхность образца. Можно считать, что в процессе деформации кристаллов за счет пинч-эффекта магнитное поле диффундирует  в кристалл, причем скорость диффузии зависит от проводимости металла и от частоты тока.

При одной и той же геометрии образцов пинч-эффект выражен сильнее на материале, обладающем высокой электропроводностью.

Таким образом, импульсный ток оказывает на деформируемый металл помимо собственно электронно-пластического действия, пондеромоторное действие, обусловленное сжатием образцов собственным магнитным полем и возбуждением в них упругих колебаний с частотой следования импульсного тока.