ФИЗИЧЕСКОЕ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ПРОВОДЯЩЕМ ПОЛУПРОСТРАНСТВЕ

Михеев В.А.¹, Пилипенко В.А.², Асмандияров И.Р.³

¹Кандидат физико-математических наук, доцент; ² кандидат физико-математических наук, доцент; ³аспирант, Тюменский государственный университет.

ФИЗИЧЕСКОЕ И МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В ПРОВОДЯЩЕМ ПОЛУПРОСТРАНСТВЕ

Аннотация

В работе реализовано математическое и физическое моделирование электромагнитного поля, генерируемого несимметричным линейным диполем в проводящем полупространстве.

Получены математические соотношения, и выполнены расчеты распределения потенциалов по длинному плечу диполя и на границе раздела проводящая среда – воздух. Измерения, выполненные с применением установки изготовленной авторами, показали качественное согласие математической и физической модели.

Ключевые слова: электромагнитное поле, разность потенциалов, диполь, моделирование, проводящее полупространство.

Mikheev V.A.¹, Pilipenko V.A.², Asmandiyarov I.R.³

¹PhD in Physics and mathematics, associate professor; ² PhD in Physics and mathematics, associate professor; ³Post graduate student, Tyumen State University.

PHYSICAL AND MATHEMATICAL MODELING OF ELECTROMAGNETIC FIELDS IN CONDUCTING HALF-SPACE

Abstract

In this work mathematical and physical modeling of the electromagnetic field generated by a linear asymmetric dipole in a conductive half-space was performed.

Mathematical relationships of a distribution of potentials on the long shoulder of the dipole and at the boundary between conductive media and air were obtained and investigated numerically. By using the experimental setup, which is made by the authors experimental data were obtained. A qualitative agreement between mathematical and physical models was shown.

Keywords: electromagnetic field, difference of potentials, dipole, simulation, conductive half-space.

Задача моделирования электромагнитных полей в проводящем полупространстве является предметом исследования многих авторов. В частности, аналогичные задачи рассматриваются в электроразведке полезных ископаемых. В последнее время такие задачи решаются чаще всего с помощью математических моделей[1,2]. Однако апробирование математических моделей на экспериментальных установках публикациям встречаются достаточно редко[3].

В настоящей работе создана математическая модель источника электромагнитного поля - несимметричного линейного диполя, помещенного в однородное проводящее полупространство.

В соответствии с теорией подобия разработана методика и изготовлены экспериментальные установки, моделирующие реальную проводящую среду.

Теоретические основы математического моделирования

Распределение потенциала и тока по диполю

Для упрощения рассмотрим поле постоянного тока, возбуждаемое вертикальным излучателем – несимметричным диполем длиной L и радиусом а, помещенным в полупространство с удельным сопротивлением

Ось z направлена вертикально вниз, нулевая отметка расположена на границе между диэлектрическим и проводящим полупространствами. Длинное плечо диполя L₁ отделено от короткого плеча диполя L₂ диэлектрической вставкой длины H. Между длинным и коротким плечами диполя включен источник тока с ЭДС ε и внутренним сопротивлением R_in (рис. 1).

Потенциал в любой точке излучателя удовлетворяет дифференциальному уравнению [4,5]:

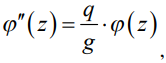                                                        (1)

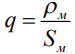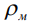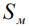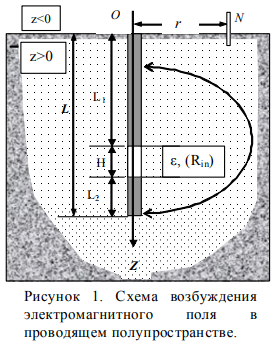
где  - линейное сопротивление проводника,  - удельное сопротивление металла,  - сечение проводника, 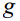 - сопротивление стеканию в пласт.

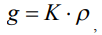                                                                         (2)

где 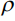 – удельное сопротивление среды,  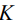– коэффициент, слабо зависящий от длины и радиуса колонны:

.

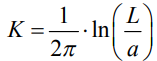Уравнение (1) следует из рассмотрения закона протекания тока по излучателю на бесконечно малом промежутке dz, который связан с разностью потенциалов dφ на концах этого промежутка соотношением:

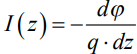                                                            (3)

Ток, стекающий в среду, с элемента излучателя длиной dz задается выражением:

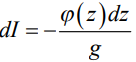 .                                                        (4)

Решение уравнения (1) для длинного плеча диполя L₁ (L₁ ≥ z ≥ 0):

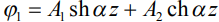,                                 (5)

для короткого плеча диполя L₂  (L ≥ z ≥ L₁+H):

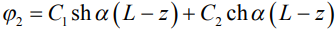,     (6)

                              (7)

Коэффициенты 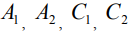 определяем из граничных условий - ток стекает с нижнего торца диполя и не течет через верхний торец диполя:

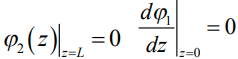                                (8)

Учтем также отсутствие тока через электрический разделитель (зазор) излучателя и непрерывность тока в источнике ЭДС:

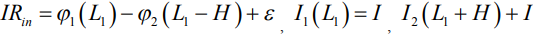.           (9)

Уравнения (8) и (9) определяют распределение потенциала и тока по длинному – 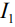 и короткому –  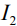плечам диполя и ток источника ЭДС –  .

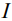Распределение потенциала по диполю будет иметь вид:

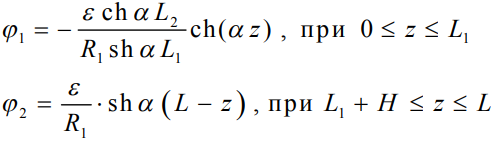                       (10)

где 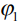 – потенциал на длинном плече диполя, а  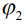– потенциал на коротком плече диполя. Коэффициент 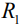определяется выражением:

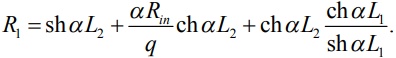                                                 (11)

Выражения для токов, получим из уравнения (3):

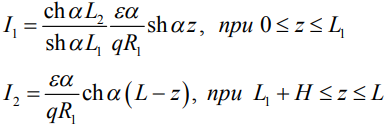                                                 (12)

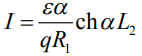.                                                                                                                    (13)

Распределение потенциала на границе раздела проводящая среда - воздух

Токи, стекающие с излучателя в окружающую проводящую среду, создают электрическое поле. Потенциал на границе раздела зависит от электрических свойств среды и удаления r от точки диполя с координатой z=0. В силу осевой симметрии, потенциал не будет зависеть от азимутального угла, а только от r и z.

Вне диполя потенциал удовлетворяет уравнению Лапласа:

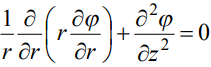.                                                                                               (14)

Потенциал поля, создаваемого элементарным током равен:

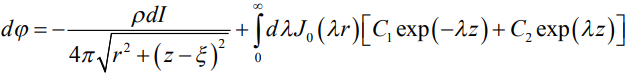,   (15)

где: 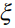 – координата элемента тока,  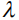– переменная интегрирования,  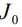– функция Бесселя нулевого порядка, 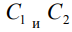постоянные интегрирования.

Производная от потенциала при z=0 равна нулю, т.к. нормальная компонента тока на поверхности раздела проводящая среда - воздух равна нулю. При условии 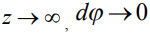  и, следовательно, 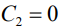. Учтем также связь:

.

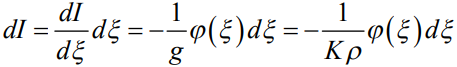Здесь воспользовались уравнением (4) для стекающего тока. Для упрощения применим известное соотношение .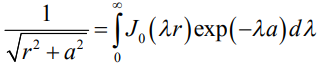

Окончательно выражение для 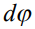 приобретает вид:

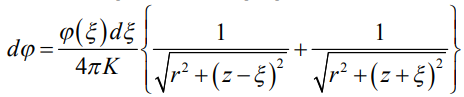                         (16)

После интегрирования (16) по всем элементарным источникам. Получим потенциал поля в любой точке (r,z) проводящего полупространства:

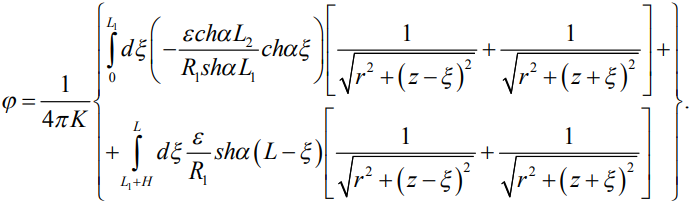           (17)

На границе раздела (z=0) на расстоянии r от диполя (17) имеет вид:

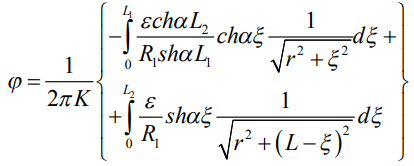                         (18)

Формула (18) применима для любых разносов r , кроме r =0.

Сравнение теоретической модели с экспериментом

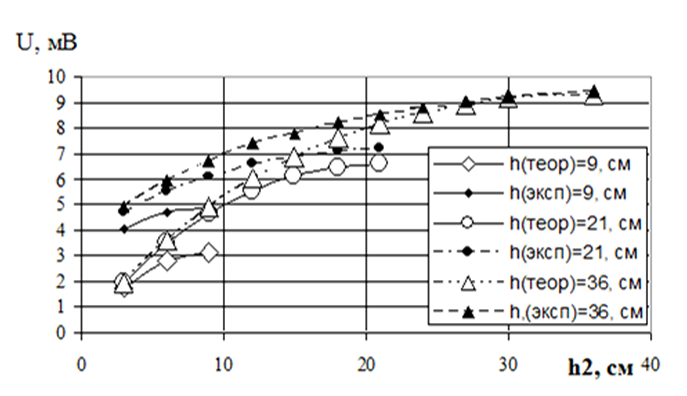
Рис.2. Разности потенциалов на длинном плече. Сравнение теории с экспериментом ЭДС 1,2 В. Экспериментальные кривые получены для переменного тока частотой 100 Гц, - теоретические кривые для постоянного тока.

С целью физического моделирования была создана экспериментальная установка, включающая в себя электролитическую ванну в форме куба с ребрами 1.5 м, заполненной водным раствором поваренной соли, источника ЭДС и приемно-регистрирующей системы. Применять источник постоянной ЭДС при физическом моделировании нецелесообразно, из-за непрерывного изменения свойств материала излучателя в результате электролиза. Поэтому в экспериментальной установке применялся генератор переменной ЭДС. Частоты выбирались исходя из теории подобия, изложенной например, в книге[3].

Результаты экспериментального исследования распределения потенциалов в сравнении с математической моделью приведены на рисунках 2 и 3.

Из рисунка 2 следует, что на малых расстояниях имеется заметное расхождение теории с экспериментом, теоретические кривые располагается ниже, чем экспериментальные. Теоретические кривые при экстраполяции, очевидно, сходятся к нулевой разности потенциалов. Экспериментальные кривые при экстраполяции также сходятся в некоторой точке, которая соответствует не нулевой разности потенциалов. Этот факт можно объяснить влиянием сопротивления подводящих проводов.

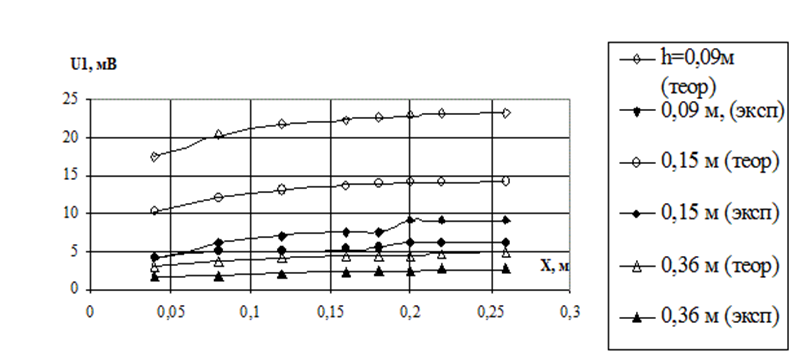
Рис.3. Графики разностей потенциалов между диполем и зондом на поверхности электролита для трех глубин погружения диполя. f=150 кГц.

Поскольку сопротивление подводящих проводов мало, его влияние на больших расстояниях от электрического разделителя уменьшается, что приводит к лучшему согласию с экспериментом. Существенной частотной зависимости распределение потенциалов по излучателю не наблюдается.

Распределение потенциалов на границе раздела проводящая среда – воздух имеет существенную частотную зависимость. Наиболее близки к расчетным экспериментальные графики, полученные при частотах поля порядка 150 кГц, что находится в согласии с формулами, следующими из теории подобия [3].

Согласно приведенным графикам на рисунке 3 , для каждой глубины графики имеют схожую форму, при заметном отличии абсолютных значений вычисленных и экспериментальных результатов. Теоретическое значение для любой глубины превышает экспериментальное, при этом различие возрастает с уменьшением глубины.

Расхождение теории с экспериментом в данном случае связано, по-видимому, с неполным соответствием математической и физической моделей и требует дополнительных исследований.