АНАЛИЗ В РАМКАХ ЛОКАЛЬНО-НЕРАВНОВЕСНОЙ ТЕОРИИ МАССОПЕРЕНОСА В ГЕТЕРОГЕННЫХ СИСТЕМАХ ПРИ ВОЗДЕЙСТВИИ КОНЦЕНТРИРОВАННЫМИ ПОТОКАМИ ЭНЕРГИИ

Волков В.А.¹, Вершинин Г.А.²

¹Аспирант; ²кандидат физико-математических наук, доцент, Омский государственный университет им. Ф.М. Достоевского

АНАЛИЗ В РАМКАХ ЛОКАЛЬНО-НЕРАВНОВЕСНОЙ ТЕОРИИ МАССОПЕРЕНОСА В ГЕТЕРОГЕННЫХ СИСТЕМАХ ПРИ ВОЗДЕЙСТВИИ КОНЦЕНТРИРОВАННЫМИ ПОТОКАМИ ЭНЕРГИИ

Аннотация

В рамках локально-неравновесной теории анализируется  неизотермический массоперенос примесных атомов в гетерогенных системах при воздействии концентрированными потоками энергии (КПЭ). Показано, что для времен наблюдения, не превышающих время релаксации диффузионного потока к своему локально равновесному значению, волновой механизм формирования концентрационных профилей является преобладающим по сравнению с диффузионным. Приводится сравнение модельных результатов с экспериментальными данными.

Ключевые слова: концентрированные потоки энергии, массоперенос, локально-неравновесная теория, моделирование.

Volkov V.A.¹, Vershinin G.A.²

¹Postgraduate student; ²PhD in Physics and mathematics, assosiate professor, Dostoevsky Omsk State University

LOCAL NON-EQUILIBRIUM THEORY ANALYSIS  OF THE MASS TRANSFER IN HETEROGENEOUS SYSTEMS UNDER CONCENTRATED ENERGY FLUX IRRADIATION

Abstract

A space-time nonlocal mass transfer of the impurity particles from the surface to the bulk of a metallic systems under the influence of the high power particles beams or the laser irradiation is analyzed. The impurity concentration profiles have been obtained on the basis of the numerical solution of the integro-differential equation for the diffusion flux. It has been shown that for the time of observation smaller than the relaxation time of the diffusion flux to its local equilibrium value, the wave mechanism of the mass transfer dominates over diffusion one. A comparison of model calculations with some of the experimental data is presented.  

Keywords: concentrated energy flows, mass transfer, locally non-equilibrium theory, modeling.

При воздействии концентрированными потоками энергии  (сильноточными импульсными электронными и ионными пучками, лазерным облучением нано - или пикосекундной длительности) в облучаемых системах генерируются сильно неравновесные поля температур и механических напряжений, которые приводят к усиленному массопереносу примесных атомов и дефектов вглубь материала, а в сплавах - дополнительно к перераспределению его компонентов. Наблюдаемые [1-3] концентрационные профили примесных атомов при высокоскоростных процессах и в малых пространственных объемах демонстрируют немонотонное поведение по глубине, характеризуемое появлением локальных максимумов на различных участках. Рассмотрение диффузионных процессов в твердой фазе в зоне воздействия КПЭ привело ряд авторов к выводу о малости диффузионного вклада в перераспределение легирующих элементов и о не диффузионной природе механизмов массопереноса [4-6]. Выяснение механизма массопереноса в металлах и сплавах в условиях импульсной обработки является важной и сложной задачей. Ее решение может способствовать более глубокому пониманию физики явления и его целенаправленному использованию для промышленной практики, т.е. представляет несомненный научный и практический интерес.

Одной из вероятных причин такой аномальной миграции атомов примеси могут быть локально-неравновесные процессы переноса. В связи с этим важным является построение эффективной и в тоже время простой теоретической модели, которая бы позволяла описывать процессы переноса в локально-неравновесных условиях. Цель данной работы состоит в теоретическом анализе в рамках локально-неравновесных теорий некоторых экспериментальных результатов по массопереносу при облучении образцов импульсными потоками энергии.

Математическая модель

Используемый в данной работе математический аппарат локально–неравновесной теории массопереноса относительно подробно описан в работах [4-6]. Там же представлены модельные расчеты концентрационных профилей примесных атомов в зависимости от набора различных параметров теории. В данной работе сопоставим предсказания модели с экспериментальными данными. Поэтому ниже приводятся только те математические выражения, которые лежат в основе моделирования.

При определенных предположениях в одномерном приближении будем рассматривать физическую систему, в которой исследуемый образец занимает полупространство 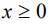. В начальный момент времени в его приповерхностном слое распределены по определенному закону примесные частицы, которые под воздействием облучения перераспределяются по глубине образца. Нагрев вещества в результате облучения учитывается наличием теплового источника 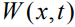, действующего в приповерхностном слое. Нас интересуют распределения примеси, формирующиеся в образце на временах, меньших или сравнимых со временем установления в системе локального равновесия. Для простоты на данном этапе анализа теплофизические характеристики среды принимаются постоянными.

Поскольку релаксация теплового потока к своему локально-равновесному значению происходит значительно быстрее, чем релаксация диффузионного потока [5,7], то будем считать, что тепловой поток определяется своим локально-равновесным значением (законом Фурье) и температура среды может описываться в приближении локального равновесия. В то же время диффузионный поток в среде в течение действия импульса эволюционирует к равновесному значению. Именно такой случай рассматривается далее [5,6].

С учетом пространственно-временной нелокальности в рамках расширенной необратимой термодинамики [7] уравнение переноса для диффузионного потока 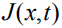 примесных атомов в гетерогенной системе с учетом термодиффузионных эффектов в одномерном приближении имеет вид [4-6]:

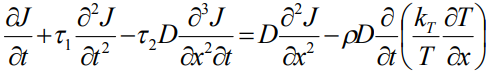,                                      (1)

где 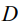 - коэффициент диффузи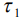и,  и 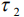 - времена релаксации плотности потока и градиента концентрации, соответственно, 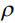- плотность среды,  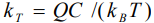- термодиффузионное отношение,  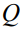- теплота переноса примеси,  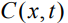- концентрация примеси,  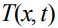- температурное поле и  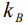- постоянная Больцмана. Переходя к безразмерным переменным (и оставляя для них прежние обозначения) 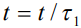,  где 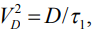 и используя закон сохранения массы в виде

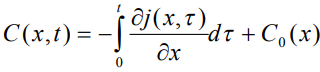                                                                                                 (2)

с начальной примесной концентрацией 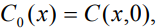 для безразмерного диффузионного потока  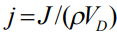получаем [5,6] замкнутое интегро-дифференциальное уравнение

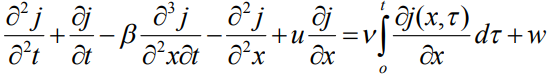                                 (3)

с дополнительными функциями

.

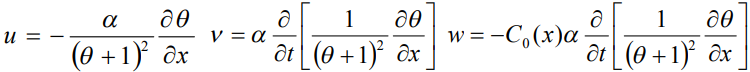Граничные и начальные условия для уравнения (3), выражающие отсутствие потока на границе и в начальный момент времени, имеют вид

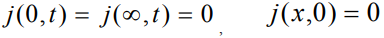.                                                                            (4)

В уравнении (3) величина 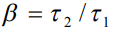 определяется отношением времен релаксаций,  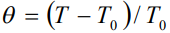- приведенная температура, 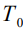-  равновесная температура среды в начальный момент времени,  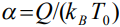- константа. При β=0 (т.е. 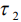= 0) уравнение (1) является гиперболическим и описывает волновой механизм массопереноса.

Для определения приведенной температуры воспользуемся локальным уравнением теплопроводности (в безразмерных координатах)

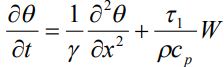,                                                                                                                      (5)

где 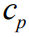 - теплоемкость,  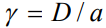и 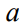 - коэффициент температуропроводности. Соответствующие начальные и граничные условия для этого уравнения выбраны в виде

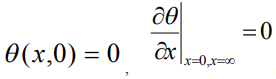.                                                                                                       (6)

Решение краевой задачи (5) - (6) дается выражением [8]:

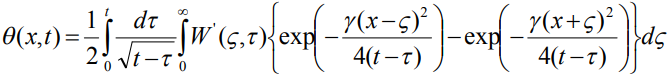,     (7)

где 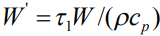 - безразмерный тепловой источник. Для определения поля температур по формуле (7) функция тепловых источников для лазерного воздействия выбиралась в форме

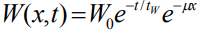,                                                                                                                            (8)

а для электронных и ионных пучков аппроксимировали в виде

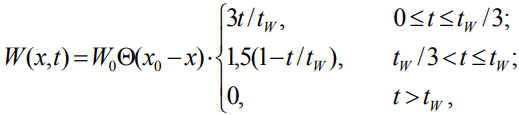                                      (9)

где Θ(x) – известная тета-функция, а параметры 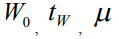 и  x₀  определяются экспериментальными условиями облучения.

Результаты моделирования

На основе найденных температурных полей строилось методом конечных разностей численное решение уравнения для диффузионного потока и далее, используя закон сохранения массы (2), - концентрационные профили. При вычислении использовались следующие фиксированные значения параметров: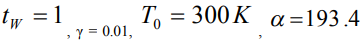. Для электронного пучка 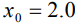, для ионного - 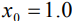, а для лазерного - .

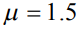На  рисунке 1  представлено  сравнение  модельных  результатов  с

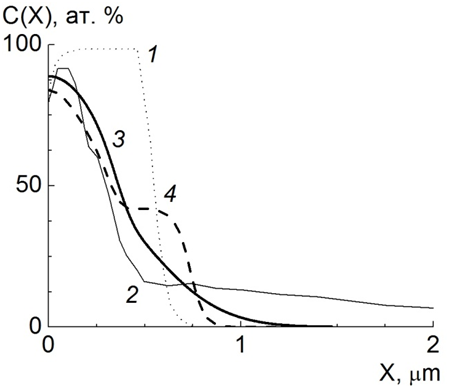
Рис.1 - Сравнение модельных и экспериментальных [1] концентрационных профилей молибдена в образце системы Mo/TiNi

экспериментальными данными.

В работе [1], в которой двухслойный образецс молибденовой пленкой толщиной 400 нм (кривая 1) на подложке из титано-никелевого сплава облучался импульсным электронным пучком с различными плотностями энергии. Исследовалось, в частности, перемешивание атомов пленки и подложки. Кривая 2 представляет сформировавшийся профиль атомов Мо после воздействия импульсным электронным пучком с плотностью энергии 15 Дж/см² (что соответствует значению безразмерного параметра 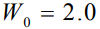). Модельные кривые 3 и 4 рассчитаны для времени наблюдения  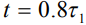с параметрами  β=0.1  и  β=0, соответственно. В данном случае расчеты с пространственно-временной нелокальностью (кривая 3) лучше согласуются с экспериментом.

На рисунке 2 экспериментальный [2] концентрационный профиль азота

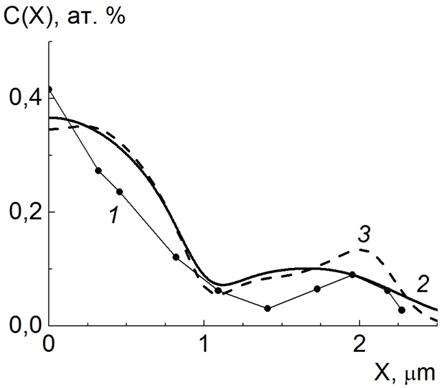
Рис.2 - Концентрационные профили атомов азота в стальном образце после воздействия на систему пленка-подложка одним импульсом мощного ионного пучка

 (кривая 1), проникшего из пленки нитрида бора в сталь-3 после облучения одним импульсом мощного ионного пучка состава 70%С⁺+30%Н⁺ с длительностью импульса 80 нс, плотностью тока 100 А/см² и энергии 1.6 Дж/см², сравнивается с модельными. Теоретические кривые 2 и 3 отвечают значениям β=0.1 и β=0, соответственно, времени наблюдения 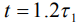, параметру  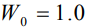и качественно правильно отражают изменение по глубине экспериментального профиля. Однако волновой механизм формирования концентрационных профилей (кривая 3) в данном случае  предсказывает лучшее согласие с экспериментом.

Сравнение модельного концентрационного профиля с экспериментальным [3] после лазерного облучения приводится на рис.3. 

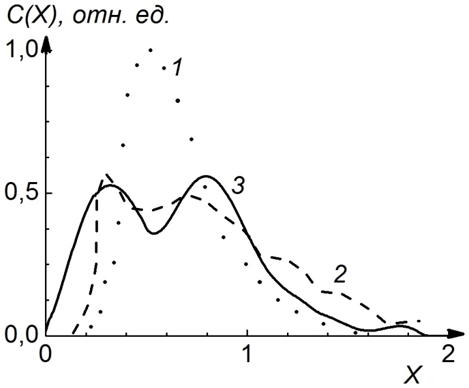
Рис.3 - Концентрационные профиля лантана в никеле

Кривая 1 представляет распределение атомов La, предварительно имплантированных в Ni с энергией 250 кэВ и дозой 1·10¹⁶ см^-2; кривая 2 – распределение атомов лантана после лазерного облучения с плотностью энергии 2.5 Дж/см² и длительностью импульса 16 нс. Исходный профиль расщепился на два пика. Модельная кривая 3 соответствует времени наблюдения 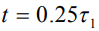, значению  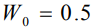без учета 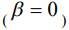пространственной нелокальности. Детальный анализ результатов моделирования [6] показывает, что при относительно малых временах наблюдения исходный пик расщепляется на два максимума (кривая 2), левый из них перемещается к поверхности, а правый -  вглубь образца. Аналогичная ситуация наблюдается экспериментально при некоторых режимах облучения импульсными сильноточными электронными пучками [9]. Если считать, что времена диффузионной релаксации в металлах составляют 10^-8 – 10^-6 с, то концентрационный профиль лантана в никеле после воздействия лазерным пучком с указанными параметрами сформирован, по-видимому, на малых временах за счет волнового механизма переноса, возникающего при релаксации системы к состоянию локального равновесия.

Таким образом, в рамках представленной модели локально-неравновесного массопереноса, индуцированного высокоинтенсивными внешними воздействиями, предсказываются концентрационные поля в гетерогенной системе, существенно отличающиеся от предсказаний локально-равновесной теории. Учет пространственной нелокальности приводит к сглаживанию волнового фронта и степень его влияния оказывается существенной при временах наблюдения, меньших и сравнимых с временем релаксации к равновесию диффузионного потока.