КИНЕТИКА ПРОЦЕССА ТЕРМООКИСЛИТЕЛЬНОЙ ДЕСТРУКЦИИ ПОЛИМЕРОВ: ПОЛУЧЕНИЕ АНАЛИТИЧЕСКОЙ ЗАВИСИМОСТИ
Тихомиров С.Г.1, Хаустов И.А.2, Попов А.П.3
1Профессор, доктор технических наук, 2доцент, кандидат технических наук, 3аспирант, Воронежский государственный университет инженерных технологий
КИНЕТИКА ПРОЦЕССА ТЕРМООКИСЛИТЕЛЬНОЙ ДЕСТРУКЦИИ ПОЛИМЕРОВ: ПОЛУЧЕНИЕ АНАЛИТИЧЕСКОЙ ЗАВИСИМОСТИ
Аннотация
В статье рассмотрено получение аналитической формы решения сиcтемы дифференциальных уравнений кинетики процесса термоокислительной деструкции полимеров в растворе. Приведено сравнение полученных результатов с экспериментальными данными.
Ключевые слова: математическое моделирование, термоокислительная деструкция.
Tikhomirov S.G.1, Khaustov I.A.2, Popov A.P.3
1Doctor Sc, Professor, 2PhD (eng), Associate Professor, 3postgraduate student, Voronezh State University of Engineering Technologies
KINETICS OF THERMAL-OXIDATIVE DESTRUCTION OF POLYMERS: OBTAINING ANALYTICAL ADDICTION
Abstract
The article considers the receipt of the analytical form solutions of differential equations of kinetics of thermo-oxidative destruction of polymers in solution. A comparison of the results with experimental data is shows.
Keywords: mathematical modeling, thermal-oxidative destruction.
Кинетика процесса термоокислительной деструкции полимера в растворе в соответствии с принятой кинетической схемой и принятых допущений [1] в общем виде описывается системой уравнений:
В уравнениях (1-4) I, D, P
– концентрация инициирующего компонента деструктора и полимера соответственно, моль/л; k2
– константа скорости образования деструктора, мин-1; k
– константа скорости деструкции, мин-1·л/моль.
Зависимость исчерпывания инициатора от времени получим интегрированием уравнения (1), с учетом начальных условий
Поскольку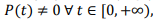 
то введя замену 
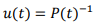, получим линейное дифференциальное уравнение общее решение которого имеет вид
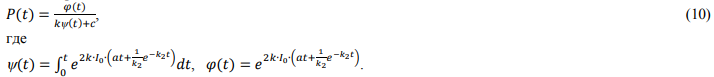
Поскольку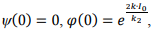 
то частное решение (9) запишется
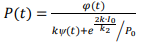(11)
Таким образом, выражения (5), (11) и (7) – являются частным решением исходной системы уравнений.
Выражения (5), (10) и (7) описывают кинетику изменения концентраций инициатора, полимера и деструктора в объеме реакционной массы в ходе реакции в изотермическом режиме, при условии, что процесс реализован в реакторе периодического действия с интенсивным перемешиванием и постоянным барботированием атмосферным воздухом.
Не смотря на то, что зависимость (11) получена в аналитическом виде, расчет кинетики производится с использованием численных методов решения, поскольку для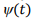 
не существует первообразной, представленной в аналитическом виде. Исходя из этого, используется один из методов численного нахождения значения определенного интеграла.
На рисунке 1 проиллюстрирован пример расчета кинетики деструкции полимера. Константы скоростей деструкции и образования деструктора были получены по результатам параметрической идентификации (11), используя интегроквадратичный критерий отклонения. В результате получены следующие оценки констант k=7,5 мин-1·л/моль, k2=7,5·10-4 мин-1. Следует отметить, что полученное значение константы скорости образования деструктора совпадает с оценками, полученными по материалам исследований, опубликованных в [2], где рассматривалась кинетическая модель изменения фракционного состава полимера в процессе деструкции при условии непрерывного барботажа реакционной массы атмосферным воздухом.
Экспериментальные данные получены с использованием метода гель-проникающей хроматографии растворов полимера, подвергающегося термоокислительной деструкции во времени. В качестве опытного материала взят каучук СКД-НД, растворенный в толуоле. Деструкцию проводили в присутствии инициатора - с массовой долей полимера в растворе – 10% и концентрацией инициатора 1,68·10-2 моль/л при температуре 60 °С.
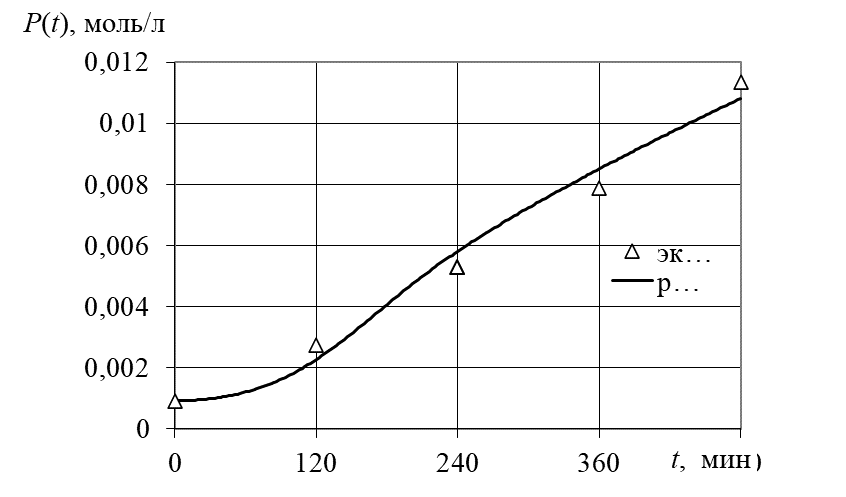
Рис. 1. Изменение концентрации полимера в процессе деструкции
Как видно из рисунка расчетные данные хорошо согласуются с данными экспериментальных исследований. Средняя относительная приведенная погрешность соответствия экспериментальным данным составляет не более 4, 2 %
Список литературы
Моделирование кинетики деструкции промышленных полимеров в растворе / В.К. Битюков, С.Г. Тихомиров, И.А. Хаустов, А.П. Попов // Материалы XXVI международной научной конференции ММТТ-26. – Нижний Новгород.: гос. техн. ун-т, 2013. – Т.3. – С.73 -76.
Усовершенствование математической модели процесса термоокислительной деструкции полимеров в растворе / С. Г. Тихомиров С. Г., И.А. Хаустов, А.А. Хвостов., А.П. Попов, Т.Н. Шеховцова // Материалы международной научно-практической конференции «Проблемы и инновационные решения в химической технологии». – ВГУИТ, 2013.