ОЦЕНКА ВЛИЯНИЯ ОРГАНИЧЕСКИХ ВЕЩЕСТВ ДОЖДЕВОГО СТОКА НА КАЧЕСТВО ВОДЫ МОРСКИХ АКВАТОРИЙ

Земляная Н.В.¹, Федоренко С. В.²,

¹Доктор технических наук, профессор; ²аспирант, Дальневосточный федеральный университет

ОЦЕНКА ВЛИЯНИЯ ОРГАНИЧЕСКИХ ВЕЩЕСТВ ДОЖДЕВОГО СТОКА НА КАЧЕСТВО ВОДЫ МОРСКИХ АКВАТОРИЙ

Аннотация

Для моделирования распространения органических загрязнений использовался модифицированный метод блуждающих частиц. Численный эксперимент использовался для получения уравнений регрессии, которые позволили оценить вклад дождевого стока в формирование поля концентраций полного биохимического потребления кислорода_.

Ключевые слова: имитационное моделирование, биохимическое потребление кислорода, регрессионный анализ.

Zemlyanaya N.V.¹, Fedorenkon S.V.²

¹Doctor of technical Sciences, professor, ²postgraduate student

Far Eastern Federal University

Estimation of influence of organic substances of a rain drain on quality of water of sea water areas

Abstract

The modified method of random walking particles has been used for simulation of organic pollution distribution. Numerical experiment was used for reception of the regress equations which have allowed to estimate the contribution of a rain drain to formation of a concentration field of the full biochemical oxygen demand.

Keywords: imitating simulation, biochemical oxygen demand, regression analysis.

Российское экологическое и санитарное законодательств по охране водных объектов от загрязнения предъявляет достаточно жесткие требования к составу любых сточных, в том числе дождевых вод. В черте населенного пункта, расположенного на морском побережье, любые сточные вода должны очищаться по всем ингредиентам до предельно-допустимых концентраций (ПДК) морской воды. В Приморском крае все реки и заливы являются водоемами и водотоками рыбохозяйственного значения, для которых ПДК имеют весьма низкие значения.

Дождевые сточные воды, являющиеся одним из доминирующих источников загрязнения, могут быть сброшены в водоем в черте города с концентрацией, например, по нефтепродуктам – 0,05 мг/л, СПАВ – 0,1 мг/л, БПК₂₀ -3 мг/л. Достижение таких концентраций на современных очистных сооружениях является достаточно дорогим процессом как со строительной, так и с эксплуатационной точек зрения. Если очистные сооружения городских сточных вод, как правило, выносят за пределы городской застройки, то дождевые сточные воды сбрасываются по бассейнам стока в пределах населенного пункта, за редким исключением, без какой-либо очистки.

Цель предлагаемой работы – определить влияние органических веществ дождевого стока на изменение экологического состояния морских акваторий.

За формирование поля концентраций загрязняющих веществ несут ответственность адвекция (перенос с течениями), турбулентная диффузия,  процессы деструкции и трансформации загрязняющих веществ.

В мелких акваториях суммарные течения определяют остаточные и ветровые течения. Роль приливно-отливных колебаний незначительна.

Для расчета ветровых течений в акватории использовалось проинтегрированные по глубине уравнения движения и неразрывности Н.Е. Вольцингера  и Р.В. Пясковского. Для глубин больших 3-10 м  нелинейные члены уравнений движения имеют больший порядок малости по отношению к нестационарным членам, поэтому для расчета течений принимались линеаризованные уравнения мелкой воды.

Задача решалась методом конечных разностей. Численная аппроксимация уравнения осуществлялась по явной схеме, разработанной В.А. Ганзеном.

Для моделирования процессов диффузии загрязняющих веществ используется модифицированный метод блуждающих частиц, использующий стохастические представления метода Монте Карло [1, 2]. Двумерная задача имитационного моделирования решалась для мелкого моря в координатах Лагранжа. К очевидным достоинствам имитационного моделирования следует отнести возможности блочного построения модели и комплексного учета многочисленных факторов, определяющих качество среды; возможность синтезировать модели, отражающие пространственно- временную изменчивость природных параметров и стохастический характер многих элементарных явлений.

В методе случайных блужданий при последовательном расчете перемещения частиц формируется кусочно-ломаная аппроксимация их траектории. Пространственное распределение конечных точек траектории достаточно большого ансамбля частиц, каждой из которых приписывается определенная масса, пропорционально вероятности попадания частиц в ту или иную точку области, а, следовательно, и концентрации загрязняющих веществ в этой точке. Понятие «условная частица» включает в себя такие свойства примеси, как пассивность и постоянный закон трансформации во время счета. Эти условия предполагают, что при моделировании все частицы примеси равноправны.

Турбулентное рассеивание примеси моделировалось с помощью случайных чисел, распределенных по нормальному закону с математическим ожиданием m = 0 и среднеквадратичным отклонением σ. Поступление примеси от непрерывно действующего источника i по загрязнению j считалось дискретным процессом поступления частиц маркеров мощностью

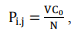                                                       (1)

где P_i,j, кг/с, - мощность выброса загрязняющих веществ, приходящегося на один маркер; V, м³/с – объем выброса от источника; С₀, кг/ м³,- концентрация примеси в источнике; N - число маркеров на один  источник.

        Координаты i - маркера в момент времени n+1 находились из системы рекурентных соотношений 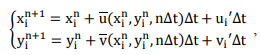[2]

                                   (2)

где 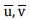- средние скорости течения; u’, v’- пульсационные составляющие скорости; ∆t -  шаг по времени.

Особенностью алгоритма численной реализации задачи было условие, заключающееся в том, что шаг по времени и вес маркера на каждом шаге принимались переменными. Для каждой координаты вычислялось время, необходимое маркеру для прохождения половины шага сетки h_x и h_y, и из этих значений выбиралось наименьшее.

Вес маркера для неконсервативной примеси на данном шаге n находился по зависимости

M=Pn∆t .                                                        (3)

Вес маркера распределялся по узлам координатной сетки. Масса загрязнения в узлах расчетной сетки Ω накапливалась, выносилась или подвергалась деструкции по мере роста времени счета и рассчитывалась в каждой точке сетки по формуле

 

 

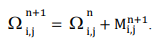                                                   (4)

 

Концентрация веществ, содержащихся в толще воды, находилась из соотношения

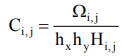                                                       (5)

В расчет вводились приливно-отливные полусуточные течения, аппроксимируемые тригонометрической функцией.

Основным достоинством предложенного в данной работе подхода была возможность моделирования пространственно-временной изменчивости поля ветровых течений. Поле ветровых течений в задаче было переменным в зависимости от характерных для каждого месяца скоростей и направлений ветра [2, 3]. Прогнозирование выполнялось при действии источников в течение теплого периода года (8 месяцев).

Синтезированная модельная задача была использована для реализации численного эксперимента при сбросе городских и дождевых сточных вод г. Владивостока в Амурский залив Японского моря (Рис.1).

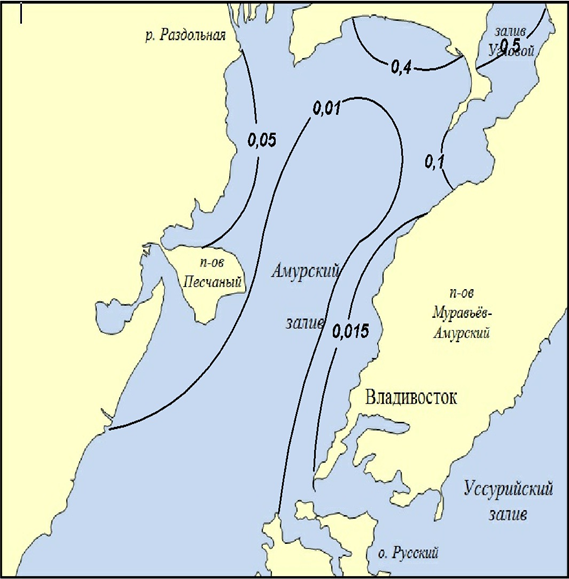
Рис.1 – Расположение источников сброса городских сточных вод; 1- район п-ва Де- Фриз; 2 – район Второй речки

 - изолинии концентраций по БПК₂₀ (сброс только дождевого стока)

Дождевые воды сбрасывались в ячейки сеточной аппроксимации рассредоточено в зависимости от площади стока и характеристики поверхности, примыкающей к береговой черте.

Концентрации сбрасываемых дождевых вод варьировались в пределах от минимальной до максимальной, характерных для реальной дождевой воды, сбрасываемой без очистки. Концентрации городских сточных вод варьировались в пределах, характерных для реальных стоков, прошедших биологическую очистку.

По генеральному плану развития г. Владивостока в Амурский залив предполагается сделать два выпуска городских сточных вод после полной биологической очистки. План предполагал расширение очистных сооружений на полуострове Де Фриз до 40 тыс. куб м в сутки и строительство очистных сооружений Второй Речки мощностью 160 тыс. куб. м в сутки на первую очередь.

Расчеты выполнялись для БПК₂₀ (биохимическое потребление кислорода за 20 дней, неконсервативный показатель) и взвешенных веществ (консервативный показатель, седиментация и агломерация не учитывались).

Имитационная модель, построенная по принципам, рассмотренным выше, дает возможность оценить качество воды в акватории при тех или иных условиях выпуска. Используя результаты моделирования, и перебирая тот или иной набор параметров сброса загрязнения, можно получить регрессионные зависимости для каждого ингредиента при любом количестве источников загрязнения.

Расчеты, проведенные для полной биологической очистки для двух источников (очистные сооружения Де Фриза завода и Второй речки), при БПК₂₀ сточной жидкости 15 мг/л и взвешенных веществах 15 мг/л, показали, что выпуски в районах Де Фриза и Второй Речки приводят к накоплению консервативных веществ в районах сброса, в северной части Амурского залива и в заливе Угловой (Рис.1). Это означает, что по консервативным веществам имеет место отсутствие равновесного состояния и все консервативные поллютанты, кроме взвешенных веществ, в этих районах могут быть сброшены с концентрацией, не превышающей ПДК, а взвешенные вещества с концентрацией, равной фоновой концентрации в заливе.

Для решения задачи по i тому веществу формируются функционалы, представляющие концентрации каждого вещества i, для каждой области повышенных концентраций k (kÎK) от набора источников n (nÎN).

В рассматриваемом случае имеется два места повышенных концентраций (K = 2) и два выпуска (N= 2), примеси присвоим номер "1", а области сброса - индекс «0».

Уравнение регрессии для БПК₂₀ при отсутствии дождевого стока, полученное в результате расчетов, в теплый период года имеет вид для первой области загрязнения (район Де Фриза)

Ф_ik =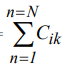 = Ф₁₁= С₁₁₁+ С₁₁₂ = 0,04С₁₀₁+0,0014              (6)

для второй (район Второй Речки)

  Ф₁₂ = С₁₂₁ + С₁₂₂  = 0,0324С₁₀₂+  0,0026 ,                              (7)

где С₁₀₁ и С₁₀₂ – концентрации по БПК₂₀ в источниках загрязнения 1 и 2.

В правой части уравнений (6) отсутствует член, зависящий от С₁₀₂, а в уравнении (7) от С₁₀₁, т.е. отсутствуют члены С₁₁₂ и С₁₂₂. Это означает, что источники сброса на Де Фризе и Второй Речке в заданном диапазоне исходных концентраций не оказывают взаимного влияния.

Будем считать дождевой сток третьим источником. Для оценки влияния на качество воды в водоеме и на формирование требований к водопользователям этого источника, были проведены численные эксперименты по определению БПК₂₀ в заливе при сбросе дождевых сточных вод. Результаты численного эксперимента показали, что дождевой сток формирует максимальное поле концентраций в ячейках с координатами x = 24; y = 24 и x = 11; y = 25, для которых примем k = 3 и k = 4 соответственно. Уравнение регрессии, учитывающее влияние дождевого стока для этих точек имеет вид

  C₁₃₃ = C₁₄₃ = 0,0012C₁₀₃ - 0,0016,                                      (8)

где С₁₀₃ – концентрация дождевого стока в источниках сброса.

На район акватории, примыкающей к полуострову Де Фриз, влияние загрязнения дождевого стока численный расчет не показал. Для района Второй Речки (К = 2) влияние дождевого стока описывается уравнением

С₁₂₃ = 0,0002С₁₀₃   ,                                                (9)

и функция Ф с учетом дождевого стока приобретает вид

Φ₁₂ = 0,0324С₁₀₂ + 0,0002С₁₀₃ + 0,0026.                        (10)

Уравнения (6-10), являются линейными, поэтому сопоставление коэффициентов регрессии дает полезную информацию на первом шаге анализа. Уравнение (10) не имеет экстремума, следовательно, допустимая к сбросу концентрация примеси определяется ограничением по ПДК.

В уравнении (10) основное влияние на качество воды оказывает сброс Второй Речки, но коэффициент регрессии перед первым членом в 162 раза больше, чем перед вторым.

Влияние второго члена находится в пределах доверительного интервала и можно утверждать, что по БПК₂₀ Амурский залив справляется с загрязнением от дождевого стока. В том случае, если бы третий источник по своей значимости был бы сопоставим со вторым, появлялась бы необходимость принятия дополнительного условия для решения задачи. В качестве такого условия могло быть технико- экономическое обоснование. В простейшем случае формирование экономической функции и ее минимизация давали бы необходимое дополнительное условие для решения задачи. Для источников примерно равной мощности в качестве дополнительного условия целесообразно принимать одинаковую степень очистки сточных вод.

Оценка влияния сброса взвешенных веществ не потребовала учета загрязнения, поступающего с дождевыми стоками, так как после расчета полей загрязняющих веществ от стационарных коммунальных выпусков стало очевидным, что сбрасывать сточные воды можно только с концентрацией взвешенных веществ, равной ПДК. Такую концентрацию можно обеспечить, подвергая дождевые сточные воды, например, полной биологической очистке. Полная биологическая очистка по экономическим показателям является слишком дорогой, особенно для региона, имеющего крайне неравномерный характер дождевого стока, поэтому более целесообразным является путь, по которому идет цивилизованное общество - организация городских территорий, исключающих загрязнение дождевого стока. Реально это означает, что в г. Владивостоке должны быть приняты неординарные меры градостроительного, правового и организационного характера.

Литература

1. Галкин Л.М. Решение диффузионных задач методом Монте-Карло. - М.: Наука, 1975. - 96 с.

2. Земляная Н.В., Ляхов В.Н. Долгосрочный прогноз качества воды в морских акваториях // Водные ресурсы. - 2003. – Т 30, № 4,. – С. 485- 492.

3. Nina V. Zemlyanaya, Vladimir N. Lyakhov. Influence simulation of solid ice on pollution distribution in marine environment // The Proceedings of the Tenth (2012) ISOPE Offshore Mechanics Symposium PACOMS –Vladivostok, 2012. - C. 186-190.