РАСЧЕТ СВОБОДНЫХ КОЛЕБАНИЙ КОРОБЧАТЫХ ПРОЛЕТНЫХ СТРОЕНИЙ РЕГУЛЯРНОЙ СТРУКТУРЫ

Соколов О.Л.¹, Ильичев Е.А.²

¹Доктор технических наук, профессор, ²кандидат технических наук, доцент, Вологодский государственный технический университет

РАСЧЕТ СВОБОДНЫХ КОЛЕБАНИЙ КОРОБЧАТЫХ ПРОЛЕТНЫХ СТРОЕНИЙ РЕГУЛЯРНОЙ СТРУКТУРЫ

Аннотация

В статье рассмотрен алгоритм расчета свободных колебаний коробчатых пролетных строений с использованием вариационной теории призматических оболочек средней длины В.З. Власова в сочетании с предлагаемым авторами решением задачи статической аппроксимации функций перемещений для конструкции, обладающей регулярной структурой.

Ключевые слова: свободные колебания, коробчатое пролетное строение, призматическая оболочка, статическая аппроксимация.

Sokolov O.L.¹, Ilichev E.A.²

Doctor of technical Sciences, Professor, ²PhD in technical Sciences, associate Professor, Vologda state technical university

CALCULATION OF FREE OSCILLATIONS OF BOX SPANS REGULAR STRUCTURE

Abstract

In the article the algorithm of calculation of free vibrations of box bridge spans using the V.Z. Vlasov variation theory of prismatic shells of average length in combination with the proposed by the authors of the solution of the static approximation of functions of displacement for design, has a regular structure.

Keywords: free vibrations, box bridge span, prismatic shell, static approximation.

Применение к расчету коробчатых пролетных строений (рис.1) технической теории свободных колебаний призматических оболочек многоконтурного сечения [1], разработанной на основе вариационной теории В.З. Власова [2] в сочетании со статической аппроксимацией функций перемещений [3], сводит задачу к решению системы вариационных уравнений динамического равновесия (1) дискретно-континуальной расчетной схемы, к которой приводится реальная конструкция (рис.2).

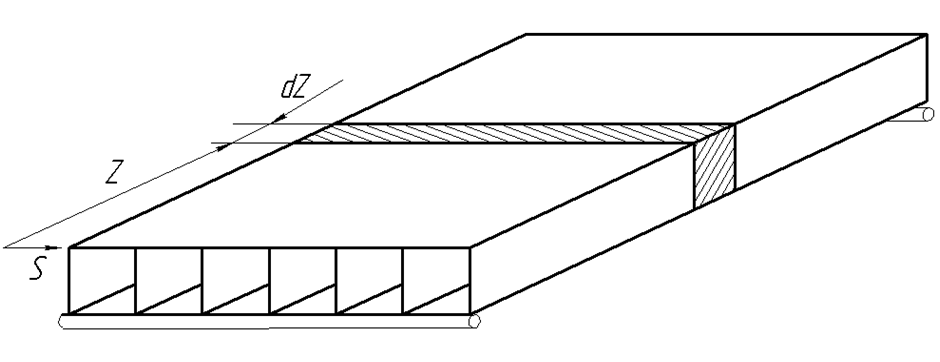
Рис.1

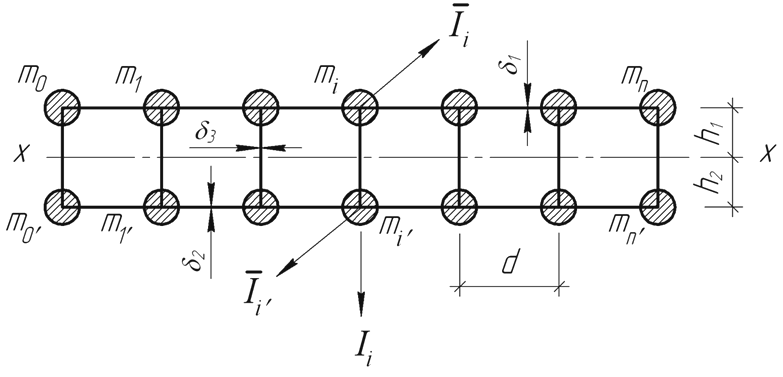
Рис.2

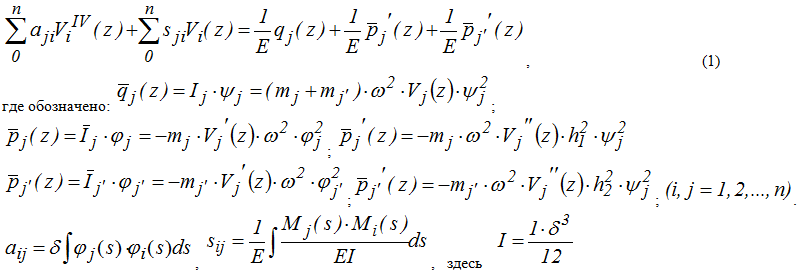
Коэффициенты и слагаемые правой части системы дифференциальных уравнений, а также компоненты частотного уравнения, полученного из решения системы (1), определяются базисными аппроксимирующими функциями перемещени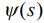й  и 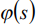. В связи с этим наиболее трудоемкая часть расчета связана со статической аппроксимацией этих функций, которые являются результатом решения вспомогательной задачи изгиба элементарной рамы-полоски от последовательного нагружения узлов сосредоточенной единичной силой.

В предлагаемом подходе к расчету свободных колебаний коробчатых пролетных строений многоконтурного сечения, обладающих регулярным строением (все ячейки имеют одинаковые размеры, толщины элементов не меняются), применяется более простой путь решения вспомогательной задачи, связанный с использованием факта регулярности структуры [3]. В этом случае составляются уравнения перемещений узлов рамы в развернутой форме, для решения которых используется математический аппарат уравнений в конечных разностях. В результате базисные функции перемещений вычисляются по замкнутым аналитическим формулам. Спектр частот свободных колебаний определяется из уравнения частот [1], а главные формы колебаний из решения системы уравнений (1).

На основе алгоритма решения разработан программный комплекс, который позволяет исследовать колебания коробчатых пролетных строений регулярной структуры (класса призматических оболочек средней длины) с любым количеством контуров в поперечном сечении, в том числе с учетом различной толщины поясов и веса дорожной одежды.

Изложенный в настоящей статье алгоритм апробирован на тестовом примере, и его результаты совпали с полученными в [1].