ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА НАНОСТРУКТУР В МОДЕЛИ ХАББАРДА

Силантьев А.В.

Старший преподаватель, Марийский государственный университет

ВЫЧИСЛЕНИЕ ЭНЕРГЕТИЧЕСКОГО СПЕКТРА НАНОСТРУКТУР В МОДЕЛИ ХАББАРДА

Аннотация

В работе представлено краткое описание приближения статических флуктуаций, которое используется при вычислении функций Грина в модели Хаббарда. Вычислены функции Грина в приближении статических флуктуаций для гексагона и пентагона.

Ключевые слова: модель Хаббарда, функции Грина, энергетический спектр, наноструктуры, гексагон, пентагон.

Silant’ev A.V., e-mail : kvvant@rambler.ru

Senior lecturer, Mary State University

CALCULATION ENERGY SPECTRUM OF NANOSYSTEMS WITHIN HUBBARD MODEL

Abstract

Short description the approximation of statical fluctuations, which adapt to calculation Green functions within Hubbard model, are given. Green functions pentagon and hexagon within Hubbard model are calculated by the approximation of statical fluctuations.

Keywords: Hubbard model, Green functions, energy spectrum, nanosystems, hexagon, pentagon.

В настоящее время большое число теоретических исследований посвящено изучению наноструктур и их структурных элементов. Для описания свойств наноструктур широко используется модель Хаббарда [1], которая применяется для теоретического описания сильно коррелируемых электронных систем [2]. При вычислении физических характеристик наноструктур в рамках модели Хаббарда используются различные приближенные методы. Нами разработано для модели Хаббарда приближение статических флуктуаций (ПСФ) [3,4], которое было предложено в работе [5] при исследовании модели Гейзенберга. В первой части данной работы кратко описано ПСФ для модели Хаббарда, а затем вычислены антикоммутаторные функции Грина и получен энергетический спектр для гексагона и пентагона, которые являются структурными элементами фуллеренов и углеродных нанотрубок [6].

       В рамках модели Хаббарда [1] наноструктуры описываются гамильтонианом вида:

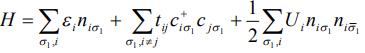                                    (1)

где 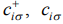 - операторы рождения и уничтожения электронов со спином  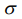на узле i;  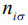- оператор числа частиц со спином  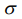на узле i; 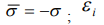- энергия одноэлектронного атомного состояния на узле i;  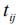 - интеграл переноса, описывающий перескоки электронов с узла i на узел j;  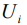- энергия кулоновского отталкивания двух электронов, находящихся на i-ом узле.

Запишем уравнение движения для оператора 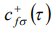, заданного в представлении Гейзенберга,

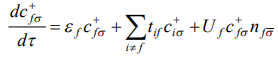                                                            (2)

где 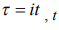 - время.

Решение уравнения (2) будем искать, используя ПСФ [4]. Следуя этому методу, оператор числа электронов 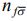 на узле f со спином  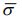 запишем в виде

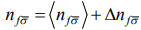                                                                (3)

где 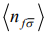 - среднее число электронов на узле f со спином  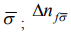- оператор флуктуации числа электронов на узле f со спином  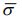, при чем предполагается, что оператор  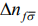не зависит от времени.

Продифференцируем по времени соотношение (3):

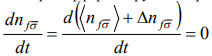                                                                                (4)

Таким образом, в ПСФ оператор 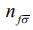 является интегралом движения. Как известно, для фермиевских операторов имеет место следующее соотношение

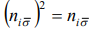                                                                                                               (5)

Умножая (2) на оператор 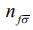 и учитывая соотношение (4) и (5) получим

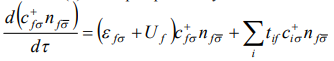                                           (6)

Аналогичным образом можно получить уравнения движения и для операторов 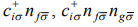,…. В результате можно получить замкнутую систему уравнений, решив которую можно найти операторы рождения.

Наиболее простым вариантом ПСФ является случай, когда оператор числа электронов не зависит от номера узла 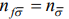. В этом случае для того чтобы получить замкнутую систему дифференциальных уравнений достаточно записать уравнения (2) и (6) для всех узлов наносистемы:

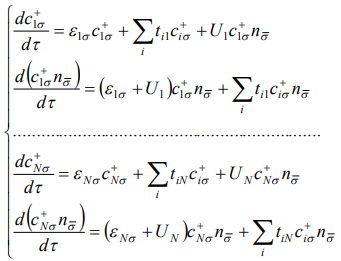                                           (7)

где N – число узлов наносистемы.

Можно показать, что решение системы из 2N дифференциальных уравнений первого порядка (7) сводится к решению системы из N дифференциальных уравнений первого порядка.

Вычислив операторы рождения можно найти антикоммутаторные функции Грина для каждого узла наносистемы. В случае, когда оператор числа электронов не зависит от номера узла 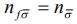, антикоммутаторные функции Грина имеют следующий вид:

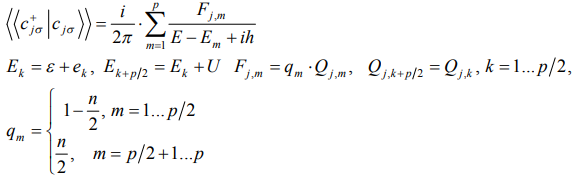         (8)

где 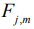 – спектральная плотность энергетического состояния 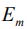, p – число энергетических состояний системы.

Зная функцию Грина можно найти энергетический спектр E_m наносистемы, спектральную плотность энергетических состояний F_j,m, степень вырождения i-го энергетического уровня g_i, а также можно определить целый ряд физических величин, характеризующих физические и химические свойства наносистемы, например, электроотрицательность по Малликену 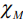, химический потенциал 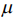, энергию ионизации 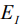, энергию сродства 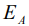, глобальную химическую жесткость  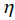, глобальную химическую мягкость  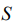и глобальную электрофильность :

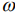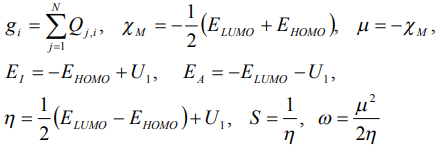                                                (9)

где 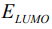 - энергия самой нижней незанятой молекулярной орбитали, а  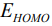- энергия самой верхней занятой молекулярной орбитали,  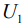- энергия, на которую смещаются  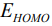и 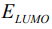 при удалении и добавлении одного электрона, N – число узлов наносистемы.

Вычислим функцию Грина для гексагона. Для этого запишем систему уравнений (6) для всех узлов гексагона

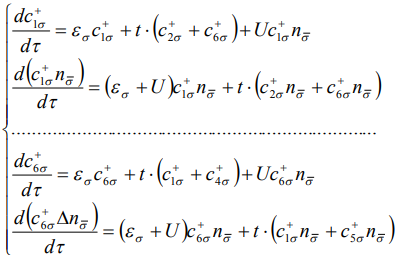                                                        (10)

Система уравнений (10) является замкнутой и имеет точное аналитическое решение. Поскольку решение является громоздким, то мы его здесь не приводим.

Для того чтобы найти спектр элементарных возбуждений в системе прежде всего вычислим фурье-образ антикоммутаторных функций Грина:

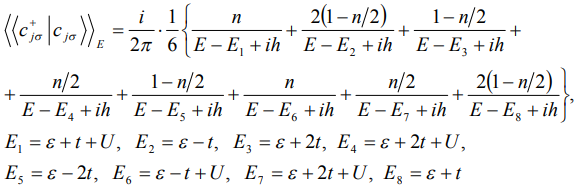        (11)

Приведем еще результаты вычислений для пентагона. Фурье-образ антикоммутаторных функций Грина для пентагона имеет следующий вид

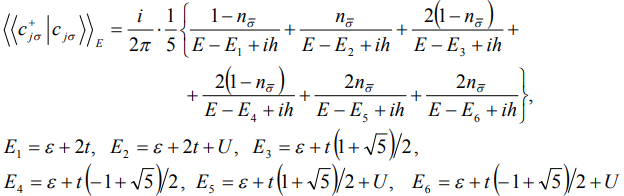         (12)

Энергетический спектр гексагона и пентагона определяется полюсами функций Грина (11) и (12).

Таким образом, предложенный в работах [3,4] метод вычисления антикоммутаторных функций Грина и корреляционных функций позволяет определять энергетический спектр наносистем в рамках модели Хаббарда, а также вычислять целый ряд физических характеристик этих систем. Отметим, что для фуллеренов С₂₀ и С₆₀ функции Грина в аналитическом виде получены в работах [7,8], соответственно.