Реализация обобщенной библиотеки для матричных вычислений на графическом процессоре для методов решения СЛАУ

Матричная алгебра неотъемлемо связана со многими прикладными областями современного технического мира, в частности, к задачам вычислительной линейной алгебры приводят вопросы, возникающие при компьютерном моделировании физических процессов, машинном обучение, обработке данных. Например, в рамках физических задач часто возникает потребность в численном решении уравнений в частных производных, для которых разработаны различные разностные схемы

Центральный процессор (CPU) хорошо справляется с обработкой матриц, но невысокого порядка. Как правило, на персональном компьютере пределом оптимальной работы матричных последовательных алгоритмов являются матрицы размера не более чем 1000 на 1000 элементов, этот предел объясняется тем, что большинство матричных операций имеют сложность более чем 

Одним из путей решения ограниченности применения матриц высокого порядка являются параллельные вычисления на графическом процессоре (GPU). Графический процессор, изначально спроектированный для работы с графикой, оказался серьезным соперником для центрального процессора в области научных расчетов.

Однако на данный момент не существует полноценных библиотек, не ориентированных на конкретную область, которые бы предоставляли многочисленный функционал для программирования матричных алгоритмов на графическом процессоре. Также нет библиотек, которые предоставляют возможность гибридной обработки матриц как на центральном, так и на графическом процессоре.

В рамках данной работы мы хотим представить подход к организации библиотеки для работы с матрицами без выделенной прикладной области, для GPU и CPU на языках программирования С/C++ и CUDA C

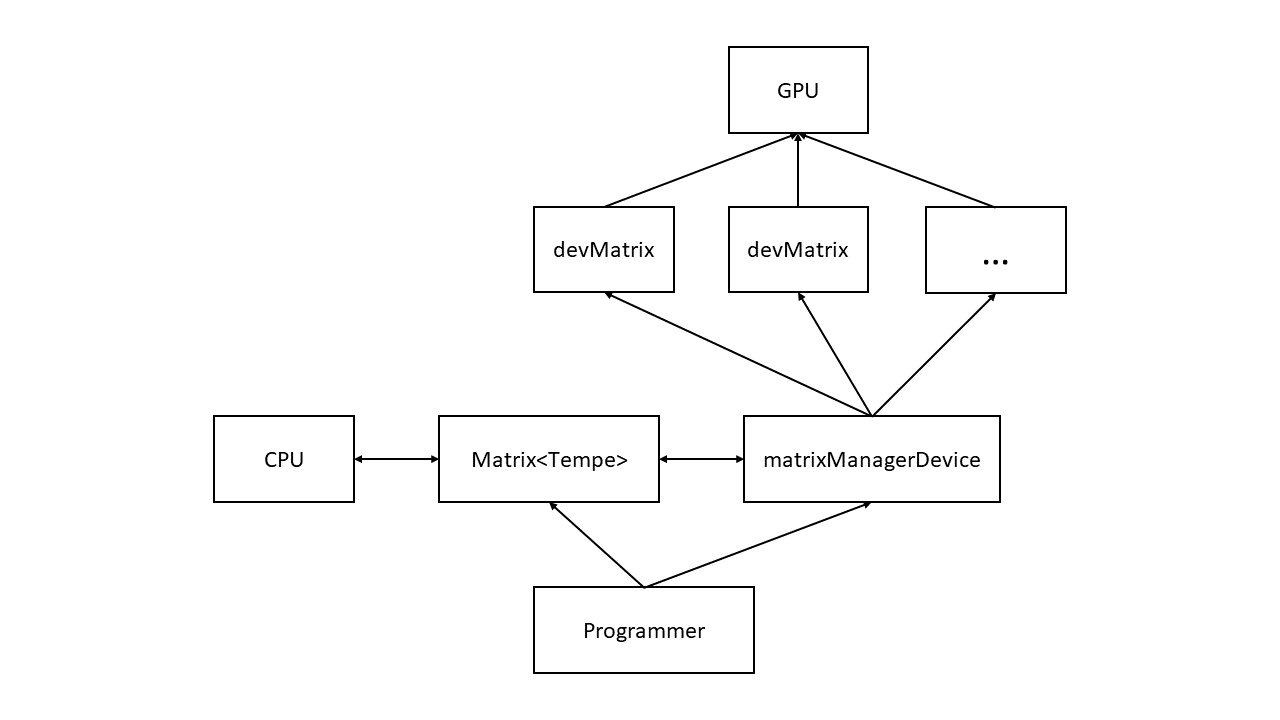
Рисунок 1 - Блок схема библиотеки

DOI:10.60797/IRJ.2025.160s.35.1

Библиотека формально состоит из двух частей (см. рис. 1). Первая — шаблонный класс Matrix для CPU, вторая — совокупность классов matrixManagerDevice, smartMatrix, devMatrix и devSparseMatrix.

Matrix<T> — шаблонный класс, представляющий CPU часть библиотеки. В широком смысле предполагается, что данный класс можно использовать не только как двумерный или одномерный контейнер чисел, но и как многомерный контейнер некоторых объектов. Многомерность достигается, как и в случае класса vector из STL C++, путем вложенности шаблонов. Например, шаблон Matrix<Matrix<double>> является представлением объекта 4-го ранга, в качестве базового типа выбран вещественный тип двойной точности. Безопасность гарантируется путем установки базовых требований к классу шаблона Matrix, в частности, сам класс Matrix удовлетворяет поставленным требованиям.

В рамках реализации Matrix, шаблоны также позволяют обрабатывать матрицы с объектами пользовательских типов, например с расширенными числовыми типами с плавающей запятой, комплексными числами и рациональными дробями. Последние в ряде случаев позволяют решать СЛАУ точными методами без потери знаков.

Иллюстрацией применения шаблонного класса Matrix является матричная свертка (конволюция), определяемая как:

где 

Операция свертки может быть представлена как умножение двух матриц 

где * — операция свертки.

Для того чтобы реализовать механизм прямого распространения в СНС, понадобится только определить специализацию оператора * для шаблона Matrix<T>, который выступает в роли изображения, и вызвать оператор * для шаблона Matrix<Matrix<T>>.

Представленный пример демонстрирует способность шаблонов к специализации кода общего назначения. Таким образом, мы хотим акцентировать внимание на том, что класс Matrix и система классов для расчетов на GPU предоставляют обширный функционал вне зависимости от прикладной области разработчика.

В ходе тестирования «автономной» реализации

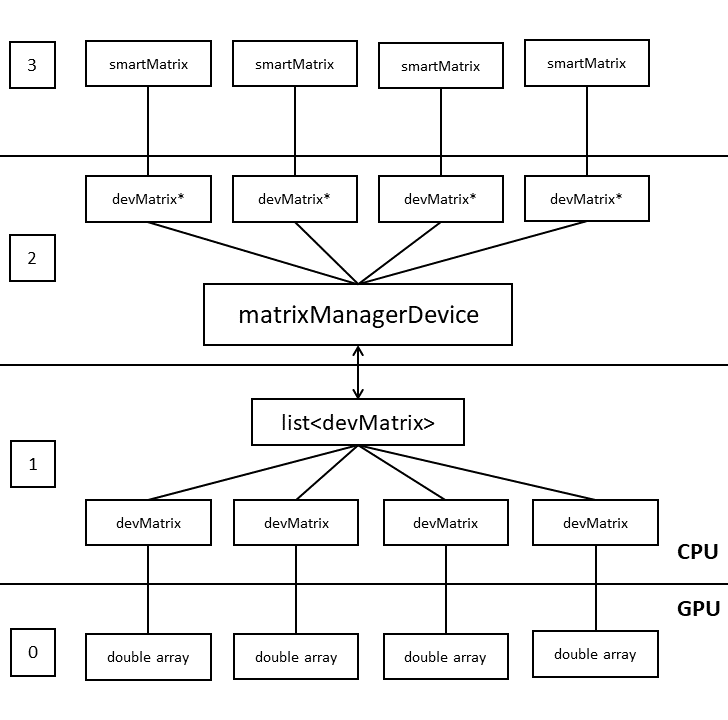
Рисунок 2 - Блок схема GPU части библиотеки

DOI:10.60797/IRJ.2025.160s.35.2

Класс matrixManagerDevice берет на себя ответственность за управление памятью. В его полях объявлен двухсвязный список объектов типа devMatrix, в свою очередь эти объекты хранят данные о матрицах, расположенных на видеокарте.

Объекты класса devMatrix имеют два состояния: первое отвечает логике активного объекта, который на данный момент участвует в вычислениях, второе состояние, напротив, соответствует «скрытой» матрице, которая готова для взаимодействия, но в данный момент в вычислениях не участвует. В случае инициализации нового объекта верхнего уровня архитектуры «скрытая» матрица проходит процедуру переинициализации и подстраивается под объект верхнего уровня.

Таким образом, в итоговой библиотеке для программиста доступно два уровня архитектуры. Первый уровень требует от программиста, понимания организации внутренней структуры библиотеки и подразумевает ручное управлением состоянием матриц, как следствие, памятью. Он предназначен для реализации высокопроизводительных алгоритмов. На его базе построены различные методы решения СЛАУ.

Второй уровень архитектуры или же высокий уровень абстракции реализован через вспомогательный класс smartMatrix, отвечающий концепции умных указателей. Класс smartMatrix обеспечивает связность библиотеки и простой синтаксис. Данный уровень предназначен для формирования математических моделей и структурных алгоритмов.

Повторное тестирование уже с применением системы классов под управлением matrixManagerDevice, показало, что резкое изменение в производительности больше не возникает, также наблюдается общий прирост скорости вычислений (см. рис. 3).

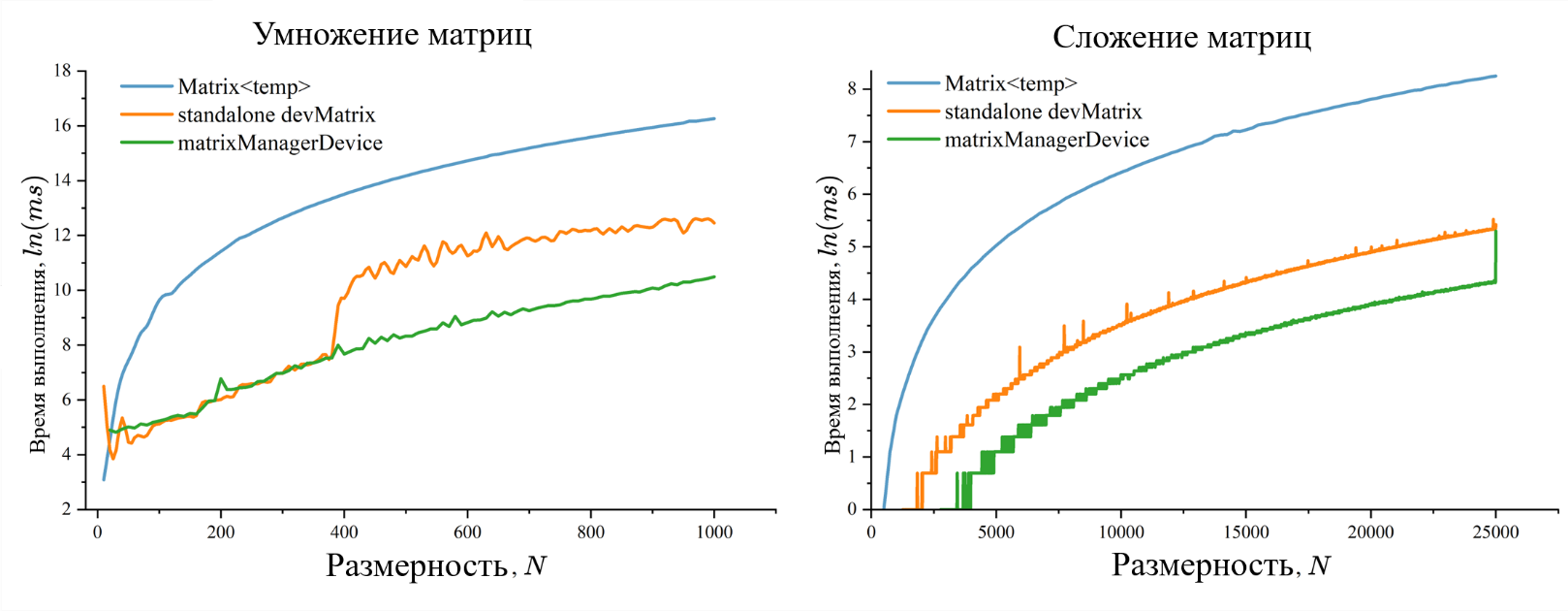
Рисунок 3 - Зависимость между временем работы алгоритма и размерностей матриц операндов

DOI:10.60797/IRJ.2025.160s.35.3

Стоит отметить, что график зависимости времени вычислений от размерности задачи в области малых размерностей имеет ступенчатый вид, связано это с перераспределением ресурсов на блоках сетки.

Описанная в предыдущем параграфе концепция matrixManagerDevice базируется на монопольном управлении ресурсами видеокарты (устройства) одним классом. Это неявно подразумевает, что класс matrixManagerDevice должен соответствовать паттерну проектирования Singleton. В действительности оказывается, что использование паттерна Singleton — это надежное решение, которое обеспечивает корректный учет памяти и эффективную загрузку GPU

При компиляции кода на языке программирования C++ компилятор преобразует шаблонный код в отдельные экземпляры шаблона, использующие различные типы. Экземпляры шаблона не взаимосвязаны между собой и воспринимаются как уникальные классы. По этой причине, если изменить реализацию статической функции, которая обеспечивает выдачу ссылки на объект matrixManagerDevice, на шаблонную с одним параметром — беззнаковое целое число, соответствующее номеру устройства, получится механизм разделения классов matrixManagerDevice, отвечающих разным устройствам, на уровне компиляции. В качестве промежуточного звена или транспортера данных выступает шаблонный класс Matrix<T>.

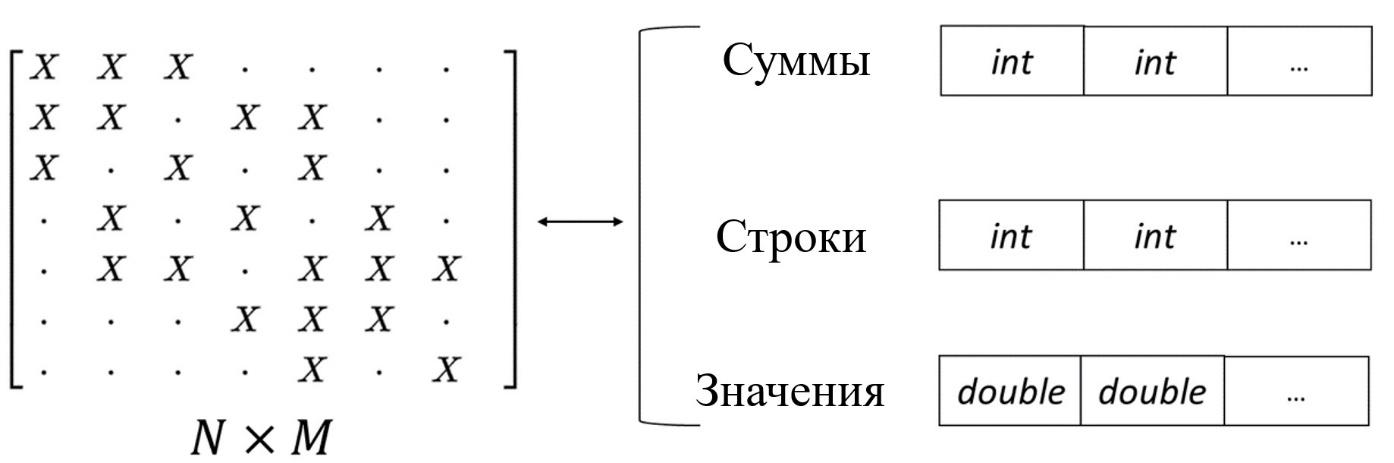
Рисунок 4 - Формат CSR

DOI:10.60797/IRJ.2025.160s.35.4

В качестве формата хранения разреженных матриц выбран CSR (сжатая разреженная строка)

[6]

. Формат CSR предполагает сопоставлять разреженной матрице три одномерных массива — сумм числа элементов строк, индексы столбцов и значения ненулевых элементов (см. рис. 4). 

Разреженные  матрицы реализованы как подчиненный matrixManagerDevice класс devSparseMatrix. Однако в реализации отсутствует концепция «скрытых» матриц, связано это с тем, что даже в рамках одной задачи размерности массивов Cumulates, Columns и Values для разных матриц могут сильно отличаться.

Применение разреженных матриц несут за собой как однозначно положительные моменты, так и отрицательные. К положительным моментам относятся: сокращение требований к глобальной памяти, уменьшается необходимый объем для хранения матриц (4). Например, матрица размера миллион на миллион с 10 ненулевыми элементами в строке в плотном формате занимает около 7.3 терабайта, тогда как в формате CSR 118.26 мегабайта. Также, что немаловажно, уменьшается число запросов к глобальной памяти устройства, что увеличивает скорость умножения матриц, как следствие скорость решения СЛАУ.

К недостаткам стоит отнести скорость построения матриц. Формат CSR подразумевает пересчет сумм числа ненулевых элементов для построения строк. Таким образом реализовать алгоритмы построения произвольных разреженных матриц с помощью функциональных объектов можно только в последовательном исполнении. Чтобы использовать GPU, необходимо для каждой математической модели строить уникальные алгоритмы, опираясь на особенности матриц.

Частично компенсирует описанный выше недостаток сохранение разреженных матриц в бинарные файлы. Чтение данных занимает сравнительно меньше времени.

В качестве инструментария библиотеки реализованы следующие алгоритмы решения систем линейных уравнений:

1) метод Крамера (CPU + GPU);

2) метод на основе LU-разложения (CPU + GPU, SparseMatrix)

3) метод покоординатного спуска (GPU);

4) метод градиентного спуска (CPU + GPU);

5) метод сопряженных градиентов (CPU + GPU, SparseMatrix)

6) стабилизированный метод бисопряженных градиентов (CPU + GPU, SparseMatrix)

В данной работе внимание акцентируется на методах 3-6, т. е. методах основанных на идеи минимизации функционала:

Где 

Одним из традиционных направлений применения методов решения СЛАУ, основанных на минимизации функционала 

Рассмотрим однородное двумерное параболическое уравнение: 

В случае неявной разностной схемы, иттерационная формула будет иметь вид:

где 

Основная матрица системы положительно определена и имеет пяти-диагональный вид (трех-диагональный для одномерного случая и семи-диагональный для трехмерного). Размеры подматриц 

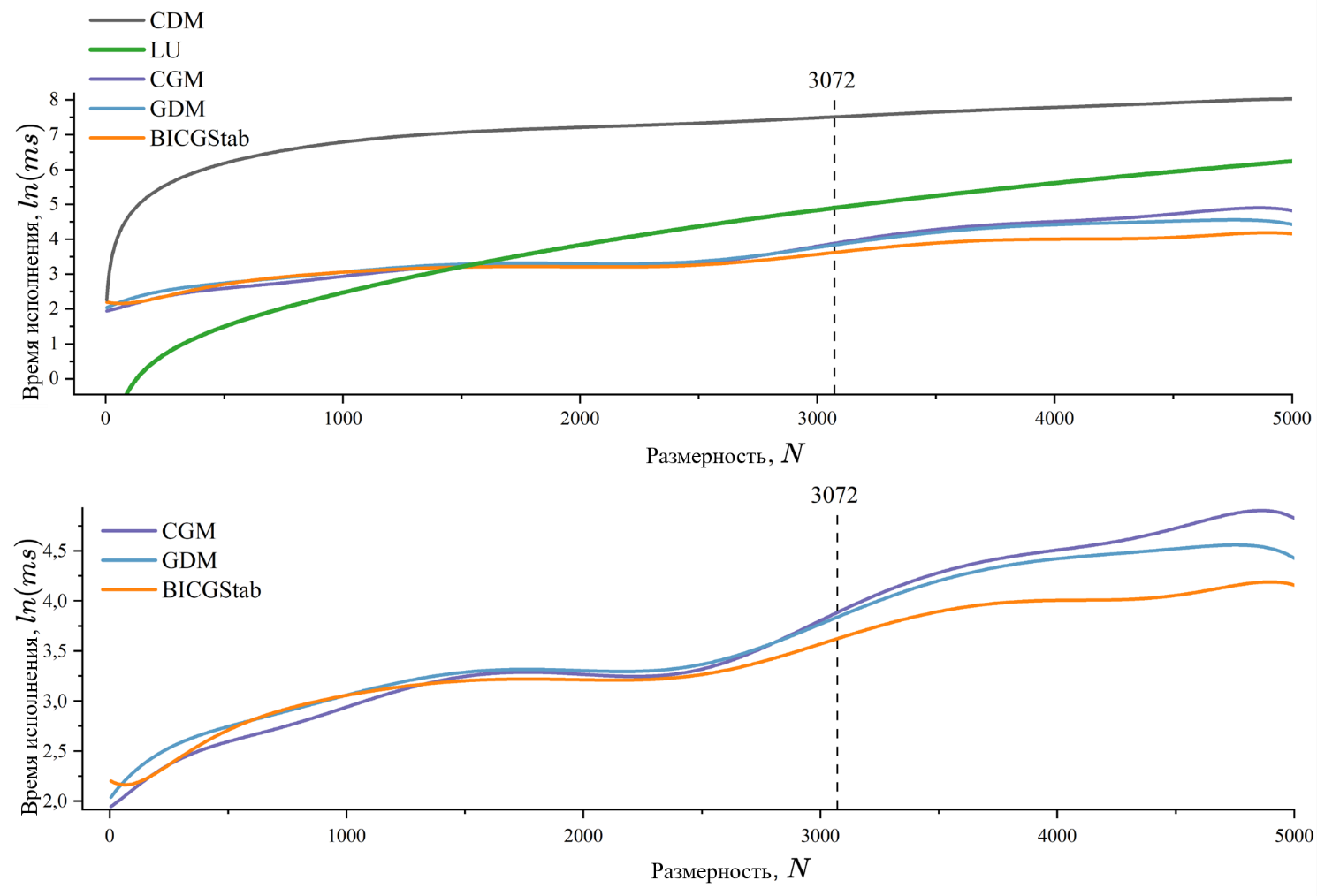
Рисунок 5 - Зависимость между временем работы алгоритмов решения и размерности задачи

DOI:10.60797/IRJ.2025.160s.35.5

В процессе решения параболического уравнения

[13]

неявной разностной схемой, проводилось тестирование производительности библиотеки (см. рис. 5).

В рамках задачи о решении параболического уравнения, самым производительным методом решения СЛАУ неявной разностной схемы является стабилизированный метод бисоппряженных градиентов, схожий качественный уровень производительности имеют методы градиентного спуска и сопряженных градиентов. Метод основанный на LU-разложении основной матрицы системы согласуется с оценочной сложностью 

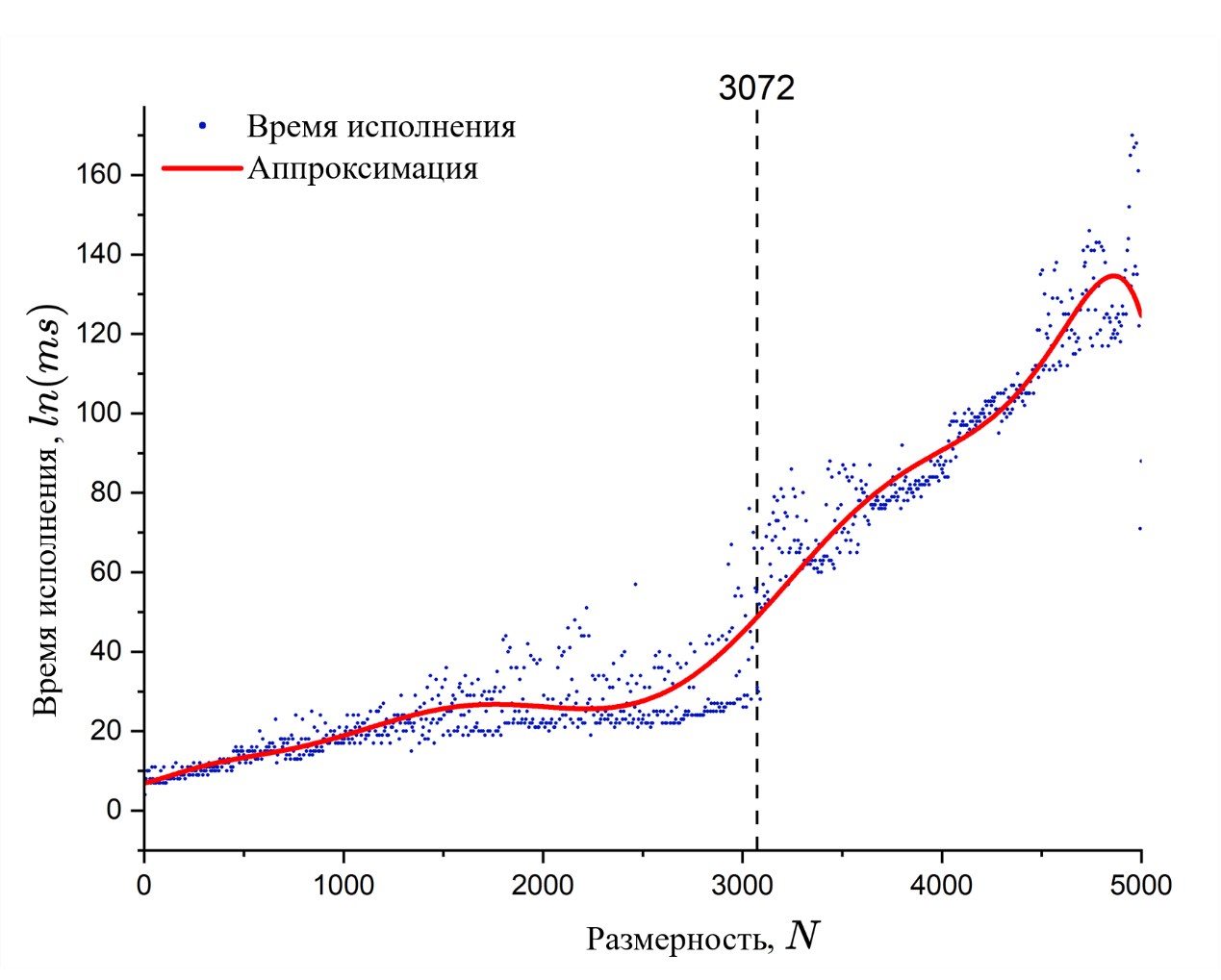
Рисунок 6 - Зависимость между временем работы алгоритма CGM и размерности задачи

DOI:10.60797/IRJ.2025.160s.35.6

Рассмотрим более подробно результат тестирования метода сопряженных градиентов (см. рис. 6).

При тестировании было замечено, что на размерности 3072 = 3 ∙ 1024 происходит значительный скачок времени решения СЛАУ методами, основанными на минимизации функционала (5). Скачок возникает из-за совокупности факторов, которые относятся как к аппаратной, так и программной части. В первую очередь на размерностях кратных 1024 происходит переопределение числа блоков, запускаемых на устройстве, в таких алгоритмах, как умножение матриц

Предлагаем рассмотреть противоположную ситуацию, т.е. решения систем с плотной матрицей (см. рис. 7).

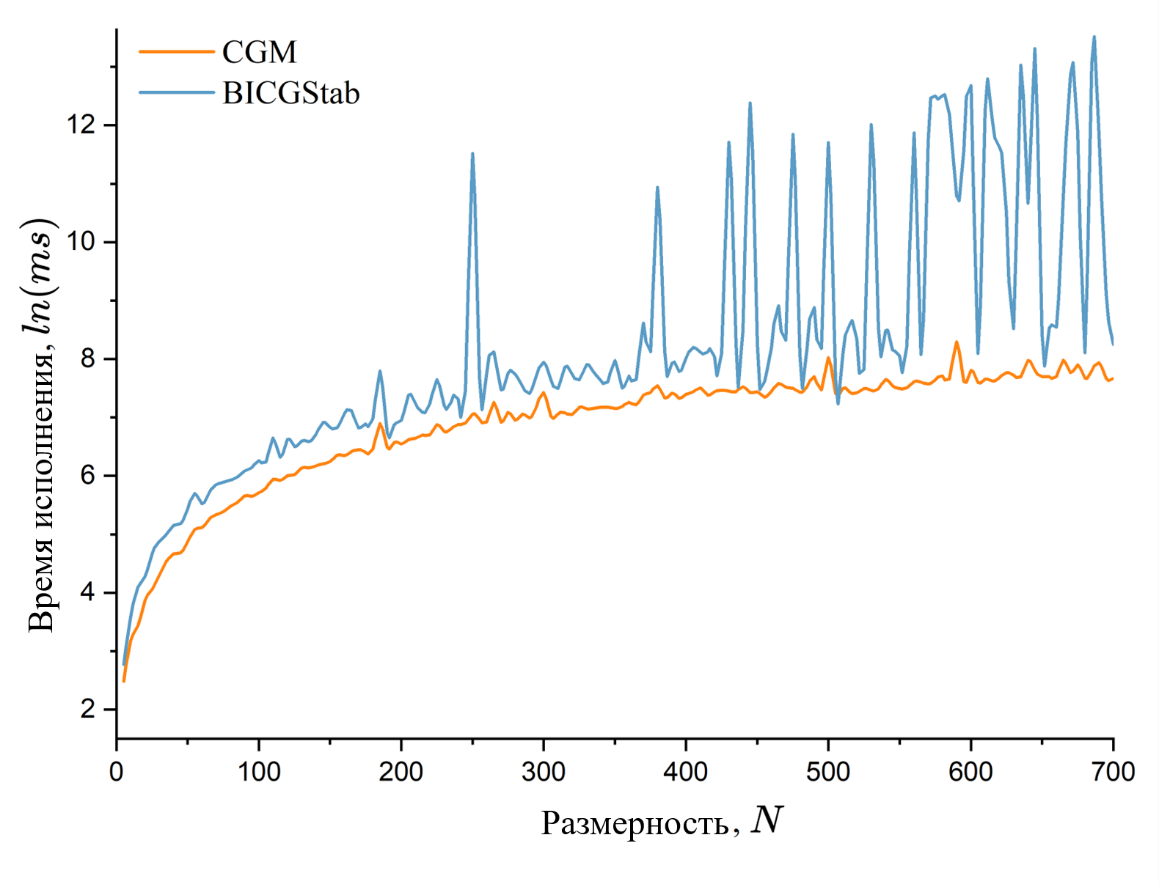
Рисунок 7 - Зависимость между временем работы алгоритмов минимизации и размерностью задачи

DOI:10.60797/IRJ.2025.160s.35.7

Наблюдается качественно схожая картина со случаем разреженных матриц (см. рис. 5), отличие заключается в порядке времени расчета. Для плотных матриц 500 × 500 время расчета находится в диапазоне 1.5-2 секунды, в зависимости от метода и критерия остановки, для разреженных матриц диапазон 14–20 мс.

Теоретически метод сопряженных градиентов ассимптотически работает за 

В данной работе описана реализация библиотеки для матричной алгебры, оптимизированной в контексте памяти для решения итерационных задач на графическом процессоре с использованием технологии CUDA. Проведенные тесты показали общее повышение производительности расчетов. Были предложены инструменты для взаимодействия центрального процессора с графическим, а также для программирования матричной алгебры на нескольких GPU.

Кроме того, в работе проведено сравнение различных методов решения систем линейных алгебраических уравнений (СЛАУ), включая методы, основанные на оптимизации. По результатам сравнительных тестов установлено, что методы минимизации применимы только к разреженным матрицам, так как на плотных матрицах из-за вычислительных ошибок они ведут себя неустойчиво. Это открывает перспективы для дальнейших исследований и оптимизаций в области вычислительной линейной алгебры, особенно в контексте использования гибридных систем CPU-GPU и разработки более устойчивых алгоритмов для работы с плотными матрицами.