Разработка эффективной модели потребления электроэнергии электромобилями

В связи с расширением автопарка электромобилей в мире и в Российской Федерации, в частности, для решения задачи по эффективному расположению электрозаправочных станций в мегаполисах, требуются современные системные подходы. Целью данной работы является исследование воздействия электромобилей на энергосистему г. Санкт-Петербурга.

Посредством программного комплекса «MATLAB» моделируется упрощённая система улично-дорожной сети города, что позволяет произвести расчеты энергопотребления в динамике роста количества электромашин.

Построение модели перемещений электроавтомобиля по городу выполним с помощью теории графов, раздела дискретной математики, который изучает графы. Граф – это множество точек (вершин, узлов), которые соединены множеством линий (ребер, дуг). Сам граф обозначим буквой G, а множества узлов и ребер между ними, как V и Е

Рассмотрим основные типы графов: ориентированный, неориентированный и взвешенный. В ориентированном графе ребрам присвоено направление, в графе без ориентации – ребра не имеют направления, во взвешенном – каждому ребру соответствует некоторое значение, называемое весом. 

Главными преимуществами теории графов являются наглядность (отображение в матричной форме) и удобство поиска минимального пути между двумя вершинами графа. Простейший граф из 6 вершин показан на рисунке 1.

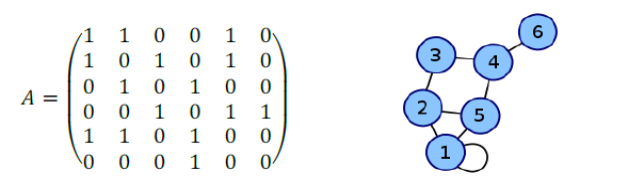
Рисунок 1 - Представление простейшего графа

DOI:10.60797/IRJ.2024.148.51.1

Разберем некоторые определения в теории графов. На рисунке 1 графи представлен в виде матрицы смежности. Это квадратная матрица, в которой значение элемента матрицы 𝑎𝑖,𝑗 равно числу ребер, выходящих из вершины графа i в вершину j. Матрица смежности простого графа определяется как бинарная матрица, содержащая нули на главной диагонали. Также возможно представление в виде матрицы инцидентности. Матрица инцидентности – это матрица, размера n x m, где n – число вершин V, m – число ребер E, элементы которой принимают значения: 𝑏𝑖,𝑗 = 1, если 𝑣𝑗 и 𝑒𝑗 соединены между собой, и 𝑏𝑖,𝑗 = 0, если между 𝑣𝑗 и 𝑒𝑗 отсутствует связь. В дополнение вводится понятие матрицы весов. Это квадратная матрица, в которой элемент ребра 𝑤𝑖,𝑗 равен весу ребра (𝑣𝑖, 𝑒𝑗). Таким образом, для теории графов вводится широкий математический аппарат, который позволяет переводить графы в числовой вид для дальнейшего вычисления. 

Для дальнейших расчетов возьмем карту автодорог г. Санкт-Петербург, которую представим в виде неориентированного графа. Вершинами графа будут пересечения и изгибы дорог, а весами ребер графа – длины соответствующих прямых дорог. Карта реальных дорог и соответствующий ей граф представлены на рисунке 2.

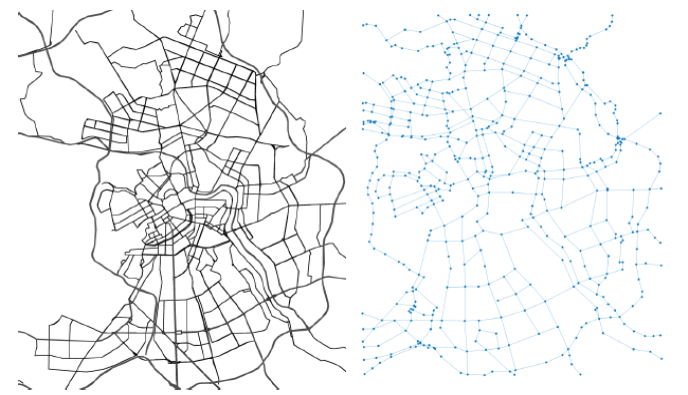
Рисунок 2 - Карта реальных дорог Санкт-Петербурга и соответствующий ей граф

DOI:10.60797/IRJ.2024.148.51.2

Граф, соответствующий г. Санкт-Петербург, включает в себя 550 вершин и практически все важнейшие связующие дороги. Перемещение электроавтомобиля по улицам опишем с помощью алгоритма нахождения кратчайшего пути. Для моделирования перемещения электромобиля в программной среде «MATLAB» воспользуемся алгоритмом Дейкстры.

Впервые алгоритм был представлен нидерландским ученым Эдсгером Дейкстрой в 1959 году

1. Инициализация. Исходный узел, от которого будет происходить поиск минимальных расстояний – начальный узел. А узел, до которого необходимо найти дистанцию – Y.

2. Все узлы обозначим как «непосещенные». Составим набор из таких узлов и назовем его U.

3. Присвоим временное значение расстояния каждому узлу. Для начального узла оно будет равным 0, для всех остальных – бесконечности. Установим начальный узел в качестве текущего.

4. Произведем оценку всех «непосещенных» соседей для текущего узла и вычислим их временно расстояние до него. Проанализируем вычисленное предварительное расстояние и текущее присвоенное значение, выберем наименьшее.

5. После посещения всех соседних вершин текущего узла, отмечаем его как «посещенный» и исключаем из набора U.

6. Алгоритм останавливается в тот момент, когда Y обозначается «посещенным» или минимальное временное расстояние между узлами в наборе U принимает значение бесконечности. Для первой ситуации это означает, что расстояние между двумя вершинами вычислено, и оно является конечным. Во второй ситуации – не обнаружена связь между исходным узлом и остальными узлами в наборе U.

7. В обратной ситуации выбираем следующий узел с минимальным временным расстоянием в качестве текущего и производим повтор этапа 3. 

В нашем случае алгоритм моделирует перемещение электромобиля по самой короткой дистанции. Например, от дома до офиса для группы «Рабочий» или от текущего расположения до ближайшей ЭЗС. Модель дорог г. Санкт-Петербург подходит для данного алгоритма, так как вес ребра определяется расстоянием соответствующих спрямленных участков дорог между вершинами графа.

Иллюстрация упрощенного описания алгоритма работы разработанной модели представлена в виде блок – схемы на рисунке 3.

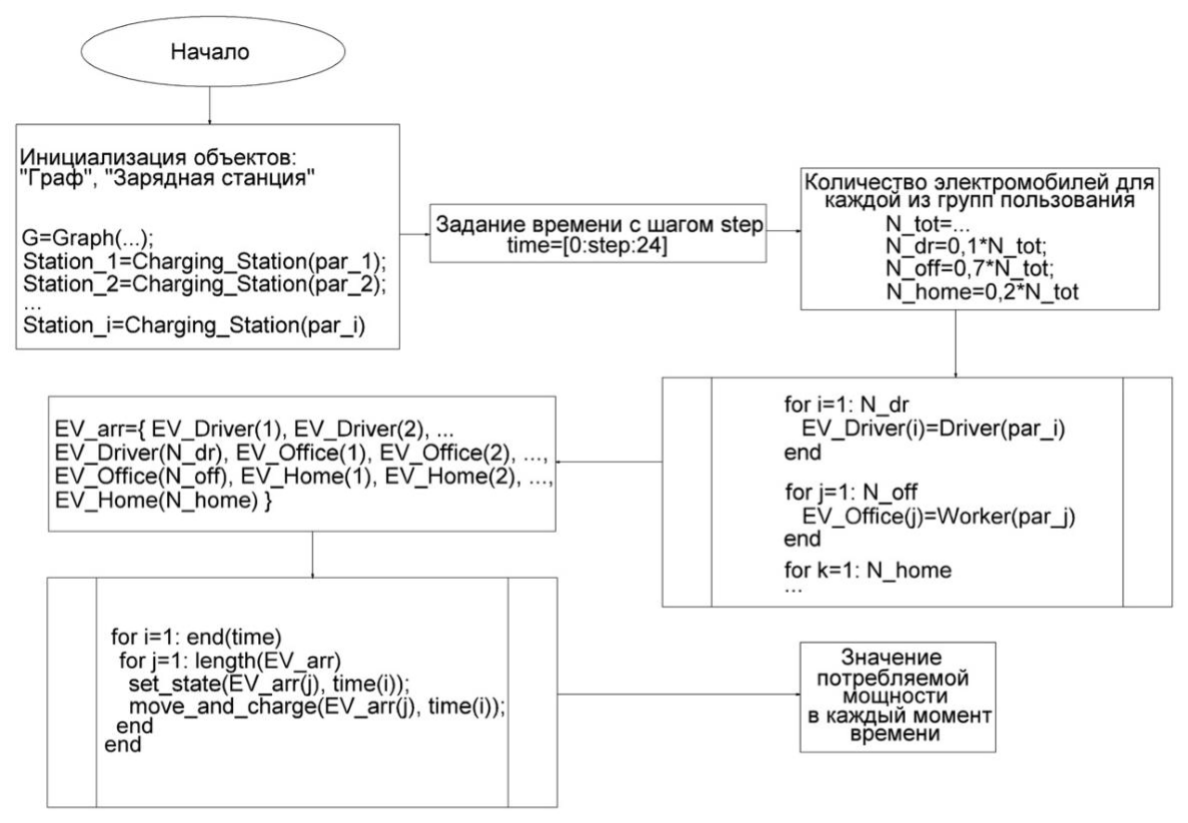
Рисунок 3 - Блок – схема разработанной модели

DOI:10.60797/IRJ.2024.148.51.3

Первые шаги модели – загрузка графа и введение объектов класса «Зарядная станция» в нужном количестве. Создается вектор времени с дискретным шагом 0,002 ч. Далее, согласно долям между подгруппами модели, вычисляется общее число электрокаров и число пользователей для каждой подгруппы.

Основной цикл – это вычисление координат и текущей скорости электрокара в каждый дискретный момент времени и вычисление величины SoC (с англ. – «state of charge» – «состояние заряда») для всех объектов класса «Электромобиль» в массиве. Происходит последовательный вызов методов данного класса: метода «set_state» для вычисления состояния электрокара в данный момент времени и метода «move_and_charge». Свойство «state» класса, которое описывает состояние электромобиля, представляется в виде строкового литерала, принимающего значения «office», «home» и «driving_home» для класса «Worker», моделирующего поведение реального работника. 

Потребляемая мощность из сети вычисляется как производная от SoC по времени, выражается в кВт∙ч.

Произведем калибровку модели, взяв за исходный граф систему дорог г. Санкт-Петербург. В начале процесса значения SoC выставляются случайным образом при помощи равномерного распределения от 0% до 100%. Для того чтобы уточнить моделирование, необходимо рассчитать характерные значения SoC для всех групп и подгрупп в начальный момент времени. Первый шаг – это выполнение пробного расчета для получения значений SoC в конце суток. Посчитанные значения принимаются как новые начальные, и расчет повторяется снова. После нескольких итераций получатся характерные значения SoC для начала расчета в каждой группе. В дополнение необходимо следовать довольно обширной выборке для получения более достоверных результатов. Таким образом, был проведен расчет, в котором количество пользователей электрокаров составило 5000.

Количество интервалов перемещения совпадает с заданным для данной модели. Форма распределения остается неизменной несмотря на то, что трафик снижает скорость в определенное время суток. Осуществим оценку потребляемой мощности в течение суток. Вычисленное значение потребляемой мощности, зависящее от времени суток, представлено на рисунке 4.

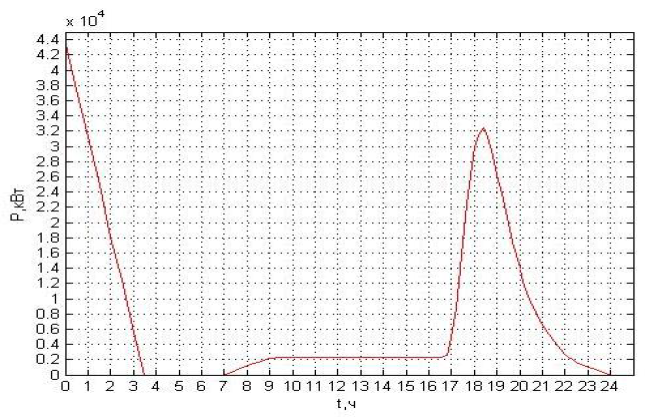
Рисунок 4 - Потребляемая мощность для N=5000

DOI:10.60797/IRJ.2024.148.51.4

В интервале от 0 до 3 часов происходит ночная зарядка дома. Из-за того, что первоначальные значения уровня заряда батареи описывались равномерным распределением, происходит постепенный «выход» из сети аккумуляторов, у которых в исходном варианте был большой уровень заряда. На интервале с 7 до 9 работники выезжают на свои рабочие места, и, так как зарядка не осуществляется, то потребление мощности из сети отсутствует. С прибытия на работу и отъезда с нее учитывается, что некоторая часть работников заряжает свои электрокары от бытовых розеток, из-за чего наблюдается постоянная величина на данном интервале. На интервале от 18 до 21 появляется «пик» нагрузки, так как произошло возвращение домой и последующая подзарядка. Полученные значения SoC в 24 часа принимаем вместо исходных и производим новый расчет. После нескольких таких итераций получим потребление мощности в течение суток, который приведен на рисунке 5.

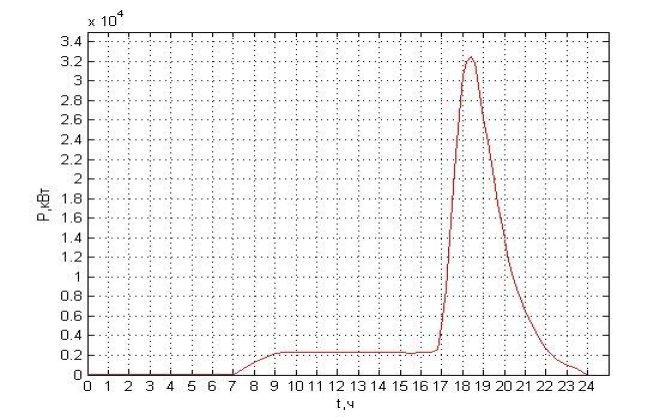
Рисунок 5 - Потребляемая мощность для N=5000 после калибровки

DOI:10.60797/IRJ.2024.148.51.5

Из рисунка 5 видно, что промежуток от 0 до 4 часов характеризуется отсутствием потребления мощности, так как батарея зарядилась до максимума на интервале от 17 до 24. Следуя из всего вышеперечисленного, заметно, что группа «Рабочий» не отличается полной разрядкой аккумулятора, так как суммарно в дороге она проводит около 2 часов, и что зарядка производится в основном от бытовых розеток. Введем допущение о том, что величина SoC для данной группы в начале расчета равна 100%, то есть полностью заряженной батарее. 

По официальной статистике ПАО «Россети Ленэнерго» в г. Санкт-Петербург и Ленинградской области сегодня работает 53 зарядные станции, 40 из которых осуществляют быструю зарядку, а 13 – медленную

Произведем вычисление потребления активной мощности г. Санкт-Петербург по приведенным выше данным. Количество электрокаров примем равным 420 шт., а число ЭЗС – 53 шт.; разместим их в соответствующие узлы графа. Получившийся нагрузка, приведена на рисунке 6.

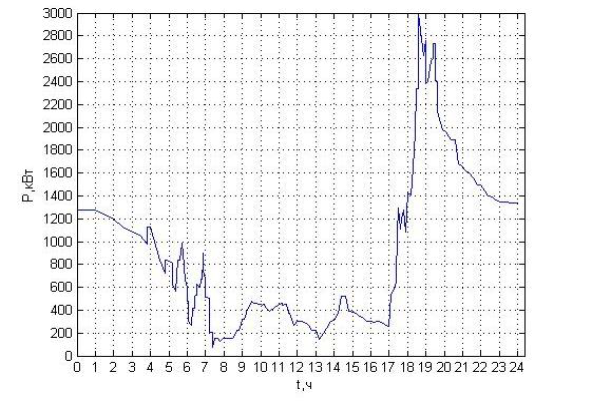
Рисунок 6 - Вычисленная потребляемая энергия для текущего числа пользователей

DOI:10.60797/IRJ.2024.148.51.6

Из графика видно, что в часы максимума нагрузки потребление равно 3000 кВт и 75 кВт в часы минимума. Оценим влияние числа электромобилей на базовый суточный график нагрузки, как среднее изменение нагрузки в каждой точки графика, используя формулу 1.

(1)

где 𝑁 – количество точек данного графика;

𝑃общ,𝑖 – общая нагрузка в i-ой точке;

𝑃баз,𝑖 – базовая нагрузка в том же месте.

 Произведя расчет по формуле 1, получаем ∆ для 417 пользователей:

Эта величина получилась довольно небольшой. График загрузки ЭЗС приведен на рисунке 7.

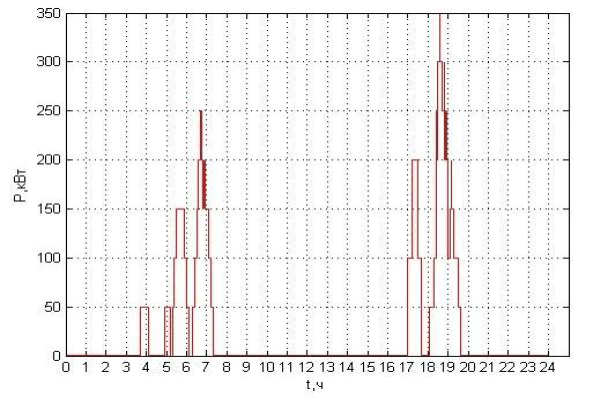
Рисунок 7 - График загрузки ЭЗС

DOI:10.60797/IRJ.2024.148.51.7

Проанализируем величину интеграла под графиком данной функции. Из расчетов в «MATLAB» она получилась равной 606,4939 кВт∙ ч. Исходя из числа ЭЗС в текущий момент – 53, числа свободных зарядных устройств – 3 и средней выдаваемой мощности – 50 кВт, получим величину загрузки ЭЗС в течение суток при 420 пользователях:

Полученное число демонстрирует, что текущее количество электрокаров в г. Санкт-Петербург не влияет существенно на график нагрузки. Отметим, что при нынешнем уровне генерации и потребления число электромобилей должно быть на порядок выше, чтобы оказывать влияние на суточный график нагрузки. Спрогнозируем, какое влияние будет оказывать увеличение количества электрокаров. Примем количества пользователей 5000,10000,15000,20000, но оставим пропускную способность сети такой же, так как данные для нее конечны. Прогноз влияния роста парка электромобилей представлен на рисунке 8.

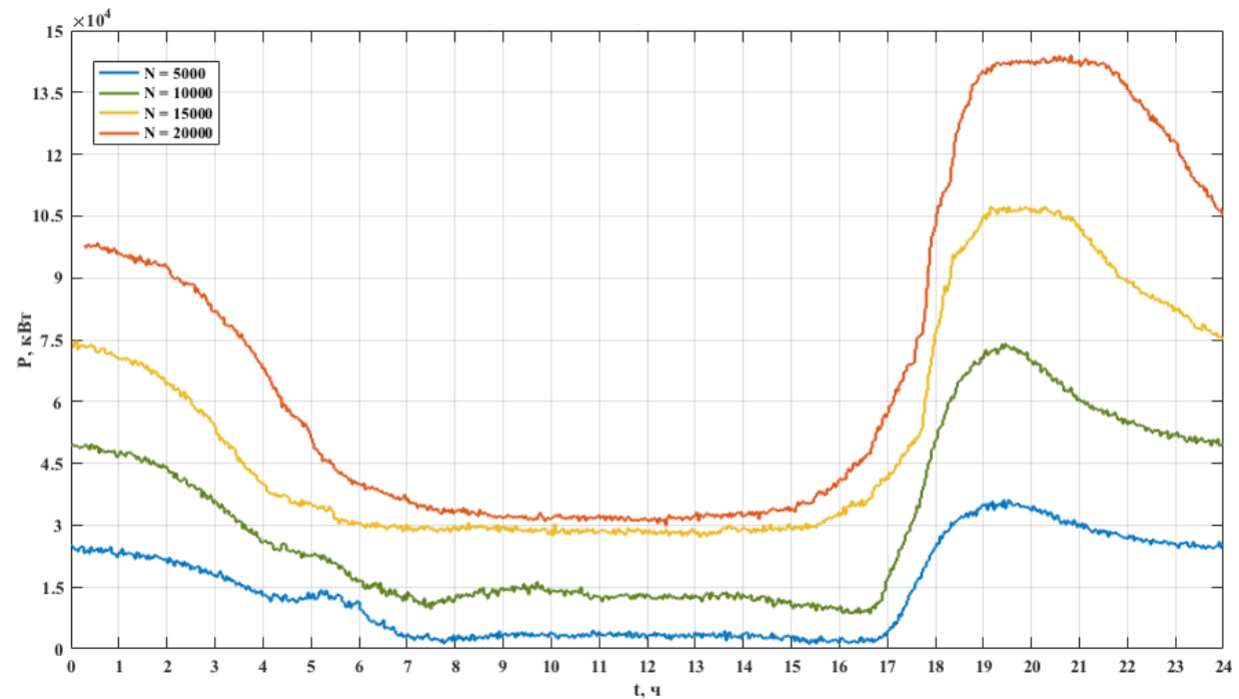
Рисунок 8 - Потребление активной мощности электрокарами с увеличением их количества

DOI:10.60797/IRJ.2024.148.51.8

Произведем оценку влияния для каждого числа пользователей:

На рисунке 9 приведен полученный график нагрузки с учетом влияния электрокаров.

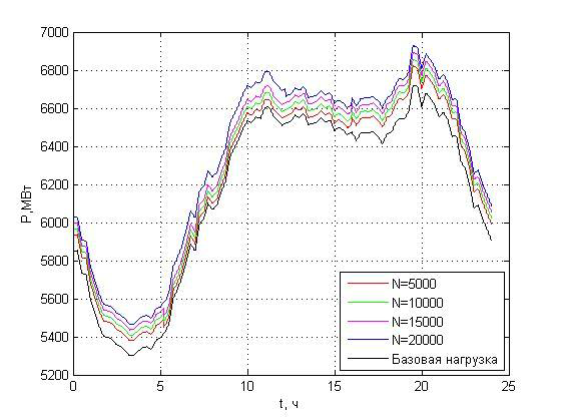
Рисунок 9 - График нагрузки с учетом влияния электрокаров

DOI:10.60797/IRJ.2024.148.51.9

Из полученного графика можно отметить значительное увеличение потребления в часы с 17 до 22 и небольшое сглаживание в часы с 1 до 5. Увеличение нагрузки ведет к увеличению расхода резервной мощности. Резервная мощность является важной составляющей управления потоками мощности в энергосистемы и состоит из нескольких элементов:

· Оперативного резерва, который необходим в случае отказа энергетического оборудования, чтобы скомпенсировать аварийное снижение мощности электростанций.

· Ремонтного резерва, который возмещает мощность оборудования, выведенного в плановый ремонт.

· Стратегического резерва, который компенсирует нарушение баланса мощности при энергетическом строительстве.

То есть расход резерва мощности приводит к уменьшению надежности энергосистемы. Необходимо отметить и нулевой резерв мощность. Баланс между потребляемой мощностью и генерируемой создается при определенной частоте данной сети. Поддержание частоты котируется повышенными требованиями, так как из-за достаточно больших отклонений может случиться выход оборудования из строя, снижение КПД двигателей, сбой технологического процесса и дальнейшую порчу конечного продукта. Для избегания всего вышеперечисленного необходимо регулировать резервную мощность и поддерживать ее на оптимальном уровне. В нашем случае нагрузка от электромобилей снижает имеющуюся резервную мощность, за счет увеличения нагрузки в пиковые часы. Однако ранее было отмечено, что мощность, потребляемая электрокарами, немного сглаживает утренний провал на графике нагрузки. Все это указывает на необходимость стимулирования пользователей производить зарядку в утренние часы для сглаживания графика нагрузки и ограничения потребления электроэнергии в часы пиков.

В данной работе был осуществлен тест модели на реальной энергосистеме города. По итогу вычислений, текущее количество электромобилей влияет на суточный график нагрузки незначительно, величина влияния равна 0,045%. При увеличении числа пользователей до 20000 данный показатель стал равен 2,142%, что уже оказывает существенное влияние.

В результате созданная модель дает возможность производить оценку потребляемой электрокарами мощности во времени и применять различные технологии по сглаживанию суточного графика нагрузки, что, в свою очередь, приводит к высокому практическому результату при проектировании системы ЭЗС.