О физической природе волн де Бройля
О физической природе волн де Бройля
Аннотация
В статье изложен новый подход к пониманию физической природы волн де Бройля и определены практические следствия такого подхода. Рассмотрено противоречие между совпадением скорости частиц – фотонов с фазовой скоростью сопоставляемых им электромагнитных волн и несовпадением скоростей поступательного движения «обыкновенных» свободных частиц (электронов, протонов и т.п.) с фазовой скоростью сопоставляемых им волн де Бройля. Обосновано значение коэффициента h/2, связывающего частоту волн де Бройля с кинетической энергией свободных частиц, рассматриваемых без их энергии покоя. Показано, что вследствие принятия коэффициента h/2, поступательные скорости движения таких частиц совпадают с фазовой скоростью сопоставляемых им волн де Бройля. Выдвинута гипотеза о том, что физическая природа волн де Бройля обусловлена воздействием только кинетической энергии свободных частиц (без учёта их энергии покоя) на структуру физического вакуума. Предложена релятивистская формула для нахождения длины волны свободной частицы с учётом только кинетической энергии и предложен метод экспериментальной проверки этой формулы в ядерной физике. В случае экспериментального подтверждения правильности названой формулы она может оказать влияние на исследования в области ядерной физики и электронной микроскопии.
1. Введение
Как известно, в 1924 году Л. де Бройль выдвинул гипотезу о всеобщности корпускулярно-волнового дуализма материи. Согласно де Бройлю, каждой частице, независимо от её природы, следует поставить в соответствие волну, длина которой связана с импульсом частицы
соотношением
(где
— постоянная Планка). По этой гипотезе не только фотоны, но и все «обыкновенные частицы» (электроны, протоны и др.) обладают волновыми свойствами , . В настоящее время корпускулярно-волновой дуализм материи является физической основой квантовой механики, согласно которой, формулы, связывающие корпускулярные и волновые свойства фотонов и «обыкновенных частиц» (электронов, протонов и др.), совершенно тождественны.
Несмотря на тождественность формул, связывающих корпускулярные и волновые свойства фотонов и «обыкновенных частиц», фазовая скорость волн де Бройля для электронов, протонов и других частиц, рассматриваемых как свободные частицы без учёта энергии покоя частицы (где,
– масса покоя частицы,
– скорость света в вакууме), ровно в два раза меньше скорости самой частицы , а с учётом энергии покоя свободной частицы её фазовая скорость превышает скорость света в вакууме , , и значительно отличается от скорости самой частицы, в то время как у фотона его скорость как частицы совпадает с фазовой скоростью электромагнитной волны, связанной с фотоном как частицей. Такая странность в отличии фазовой скорости волн де Бройля «обыкновенных» частиц от скорости самих частиц и совпадение фазовой скорости электромагнитной волны фотона со скоростью фотона как частицы, в принципе, противоречит и тождественности корпускулярных и волновых свойств всех видов материи и требует детального рассмотрения и объяснения, поэтому рассмотрим этот вопрос более подробно.
С момента теоретического обоснования Луи де Бройлем в его докторской диссертации возможности существования связанных с веществом волновых процессов физическая природа волн де Бройля остаётся не выясненной , , , их нельзя отнести ни к механическим, ни к электромагнитным волнам. Волны де Бройля не переносят энергии и не требуют среды для своего распространения . Cогласно статистической интерпретации квантовой механики, волны де Бройля имеют особый физический смысл «волн вероятности» , но именно такая интерпретация стала главным затруднением теории «волны – пилота» де Бройля, так как движением частицы управляла волна, имеющая символическое представление вероятности в пространстве и времени . В общей дискуссии после всех докладов на Пятом Сольвеевском конгрессе выступил Эйнштейн. Он одобрил попытку де Бройля приписать корпускуле некоторое место в волне. «Процесс эволюции корпускул следует описывать не только исключительно волной Шрёдингера, но, в то же самое время, локализовать частицу в процессе распространения волны. Я думаю, что де Бройль прав, ведя поиск в этом направлении» .
Однако невозможно локализовать частицу в сопутствующей ей волне, если фазовая скорость волны не совпадает с поступательной скоростью частицы, поэтому Л. де Бройль придавал большое значение установлению определённого соотношения между распространением волны, природа которой не ясна, и движением частицы. На этом пути де Бройль получил, по его словам, самое важное следствие, касающееся соотношения между скоростью частицы и скоростью связанной с ней волны. Это следствие есть равенство скоростей группы волн и частицы, оно было получено де Бройлем при рассмотрении волновых пакетов, которые образуются в пространстве при распространении фазовых волн . Однако и эта концепция де Бройля столкнулась с большими трудностями, так как в дальнейшем выяснилось, что волнам де Бройля присуща очень сильная дисперсия . Дисперсия приводит к тому, что группы волн де Бройля (волновые пакеты) расплываются со временем. Это не позволяет представлять частицы в виде групп волн де Бройля . Волновые пакеты вещества неограниченно распространяются и в течение небольшого промежутка времени способны занять очень большое пространство (до миллиардов километров) .
В современной научной литературе соотношению фазовой скорости волн де Бройля и скорости частицы в физическом пространстве или не уделяется достаточного внимания вследствие абстрактности современных интерпретаций квантовой механики, в которых исчезает и само представление о реальном физическом пространстве , или принимается точка зрения де Бройля, заключающаяся в том, что волны материи не абстрактны и существуют в реальном физическом пространстве в отличие от абстрактного конфигурационного пространства 3N измерений , , , однако, согласно трём последним указанным работам, фазовая скорость волны де Бройля в реальном физическом пространстве не совпадает со скоростью частицы .
В связи с обсуждением вопроса о совпадении скорости частицы с фазовой скоростью сопоставляемой ей волны де Бройля следует отметить работы , , в которых обосновано совпадение фазовой скорости волны де Бройля и скорости частицы
в реальном физическом пространстве.
В настоящей статье «О физической природе волн де Бройля» равенство на основании нового подхода с использованием коэффициента
будет выведено из основной формулы квантовой теории, определяющей энергию фотона,
.
В дальнейшем равенство и коэффициент
будут использованы для получения новой релятивистской формулы для длины волны де Бройля и будет показана возможность использования этой формулы в ядерной физике и электронной микроскопии.
Целью данной работы является обоснование возможности понимания физической сущности волны де Бройля как распространяющегося в физическом вакууме локализованного возмущения, обусловленного кинетической (механической) энергией частицы. Под локализованным возмущением физического вакуума понимается область пространства вокруг движущейся частицы с изменёнными кинетической (механической) энергией частицы свойствами вакуума.
2. Корпускулярно – волновой дуализм материи при рассмотрении свободной частицы без учёта энергии покоя
В случае однородной и изотропной среды вдали от зарядов и токов, создающих электромагнитное поле, уравнения Максвелла приводят к волновым уравнениям описывающим, в частности, распространение плоских волн:
Здесь и
амплитуды колебаний напряжённостей электрического и магнитного полей . Существование двух независимых друг от друга уравнений позволяет рассматривать плоскую гармоническую волну с произвольной ориентацией вектора E электромагнитной волны в плоскости волнового фронта в виде суммы двух независимых плоских гармонических волн той же частоты, что и исходная, направления колебания векторов E и H взаимно перпендикулярны . Энергия электромагнитной волны делится поровну между её электрической и магнитной составляющей .
В согласии с и фотон традиционно сопоставляется с плоской монохроматической гармонической электромагнитной волной, однако плоскую электромагнитную монохроматическую гармоническую волну допустимо представить в виде суммы двух компонент независимых плоских монохроматических гармонических электрической и магнитной волн той же частоты, что и исходная (как было отмечено выше), поэтому фотону могут быть сопоставлены две плоские гармонические бескомпонентные (т.е. не имеющие составляющих) электрическая и магнитная волны.
Так как фотон допустимо сопоставить с двумя плоскими бескомпонентными волнами, энергии которых равны друг другу, то в рассматриваемом случае энергия каждой плоской электрической и магнитной волны равна половине энергии фотона, т.е.
где и
– энергия, сопоставляемых с фотоном, соответственно электрической и магнитной волн;
– линейная частота монохроматической электромагнитной волны;
– линейная частота электрической волны;
– линейная частота магнитной волны.
При этом должно выполняться равенство
Но выполнение равенств (1) и (2) возможно только в том случае, если коэффициент пропорциональности, связывающий частоту плоских электрической и магнитной волн с половиной энергии фотона равен , т.е.
Суммирование равенств (3) и (4) при условии выполнения равенства (2) даёт
где – энергия плоской монохроматической электромагнитной волны, сопоставляемой фотону.
При сопоставлении фотона с плоскими бескомпонентными электрической и магнитной волнами элементарным квантом действия оказывается величина (как это следует из соотношений (3) и (4)), а величина действия
, как следует из соотношения (5), является суммой элементарных действий
. Оказывается, что квант действия
, обнаруженный экспериментально, справедлив по отношению к фотону вследствие физической сущности электромагнитных волн, у которых частота колебаний монохроматической электромагнитной волны совпадает с частотой колебания составляющих её электрической и магнитной волн. Уравнения (3) и (4) физически справедливы, так как электрические и магнитные волны являются реальными физическими объектами – компонентами электромагнитной волны, и сопоставляются они с реальными физическими объектами – электрической и магнитной компонентами энергии фотона. Итак, совпадение частоты результирующей волны с частотами двух волн, являющихся компонентами результирующей волны, является необходимым условием появления постоянной
.
Так как в данном разделе статьи мы рассматриваем свободные частицы без учёта энергии покоя, то они имеют только кинетическую энергию и, следовательно, энергия таких свободных частиц не имеет компонент, в этом смысле они являются бескомпонентными частицами (в отличие от фотонов, которые имеют две компоненты энергии – электрическую и магнитную), поэтому свободным частицам в рассматриваемом случае должна быть и сопоставлена бескомпонентная плоская гармоническая волна, частота колебаний которой в согласии с соотношениями (3) и (4) связана с энергией волны (или с энергией сопоставляемой ей свободной частицы) коэффициентом . Возможно, что это один из основных законов природы.
Если рассматриваемой в данном разделе статьи свободной частице сопоставить плоскую бескомпонентную гармоническую волну, угловая и линейная
частоты которой связаны с энергией частицы
коэффициентами соответственно
и
, то соотношение
, , справедливое по отношению к фотону, для свободной частицы, имеющей только кинетическую энергию, следует записать в виде
Так как энергия свободной частицы в данном случае равна её кинетической энергии, то (6) при условии
запишем в виде
где – масса покоя свободной частицы;
– поступательная скорость движения свободной частицы в данной инерциальной системе отсчёта (ИСО).
Для удобства дальнейших рассуждений будем рассматривать движение свободной частицы в ИСО, связанной с физическим вакуумом. Мы рассматриваем физический вакуум, как реальную физическую среду, проявляющую своё существование в таких явлениях как, например, эффект Казимира и лэмбовский сдвиг атомных уровней. При этом физический вакуум не имеет массы покоя, т.е. является невещественной материальной средой (поскольку под веществом понимается материя, имеющая массу покоя). На возможность связи ИСО с невещественной структурой физического вакуума указывает также открытие космического микроволнового фонового излучения (КМФИ), однородно и изотропно заполняющего всё пространство Метагалактики и имеющего температуру 2,725К, что позволяет рассматривать КМФИ как фотонный газ . Результирующая векторная скорость фотонов относительно физического вакуума в этом случае равна нулю, т.е. фотонный газ, рассматриваемый как некоторая среда, покоится относительно невещественной структуры физического вакуума и поэтому как с КМФИ, так и с физическим вакуумом может быть связана ИСО . Фотоны не имеют массы покоя, как и физический вакуум, но фотонный газ имеет температуру отличную от абсолютного нуля и это обстоятельство позволяет экспериментально обнаружить движение инерциальных систем, в частности Солнечной системы, относительно фотонного газа и, следовательно, относительно структуры физического вакуума .
Вернёмся теперь к соотношению (7). Так как линейная частота волнового процесса равна отношению фазовой скорости волны
к длине волны
, то (7) запишем в виде
Из уравнения (8) при равенстве поступательной скорости частицы и фазовой скорости
бескомпонентной плоской волны, сопоставляемой рассматриваемой свободной частице, следует формула для длины сопоставляемой частице волны
Соотношение (9) представляет собой известную формулу де Бройля. Если в (8) вместо постоянной положить постоянную
, то для получения формулы де Бройля (9) необходимо будет принять, что
Именно такое значение указано в .
Таким образом, принятие значения постоянной позволяет избежать противоречия между совпадением фазовой скорости электромагнитной волны фотона со скоростью фотона как частицы и отличием ровно в два раза фазовой скорости волн де Бройля других частиц (электронов, протонов и др.), рассматриваемых как свободные частицы без учёта энергии покоя, от скорости самих частиц. Такое отличие в принципе противоречит и корпускулярно – волновому дуализму материи, предполагающему максимальную тождественность корпускулярных и волновых свойств всех видов материи.
Совпадение фазовой скорости волн де Бройля со скоростью поступательного движения частиц материи, обоснованное в данной статье, позволяет наполнить идею де Бройля о волне - пилоте новым содержанием. При принятии постоянной фазовая скорость волны де Бройля совпадает со скоростью поступательного движения самой частицы и вследствие этого отпадает необходимость представлять частицы в виде групп волн де Бройля. Появляется возможность рассматривать волну де Бройля как некоторое реальное локализованное возмущение в невещественной структуре физического вакуума, превышающее размеры частицы и сопровождающее её движение. Подобно этому и с фотоном, как частицей, связана некоторая локализованная электромагнитная волна, распространяющаяся со скоростью частицы – фотона, и представляющая собой определённое возмущение в невещественной структуре физического вакуума.
Используя уравнение (8), запишем в релятивистской форме значение кинетической энергии частицы для нахождения в этом случае длины волны де Бройля
при значении постоянной
и равенстве скорости
частицы фазовой скорости сопоставляемой ей волны
Из (11) при следует формула для
:
Формула (12) при переходит в формулу (9).
Возникает вопрос, какой смысл заключается в том, чтобы рассматривать корпускулярно – волновой дуализм свободной частицы без учёта её энергии покоя? Оказывается, что именно такой подход позволил Шрёдингеру получить нерелятивистское уравнение (впоследствии названное уравнением Шрёдингера), являющееся основным уравнением нерелятивистской квантовой механики, при этом, как известно, в уравнении Шрёдингера понятие энергии покоя не используется, а используются только понятия кинетической и потенциальной энергии. Частным случаем уравнения Шрёдингера является дифференциальное уравнение, которому должна удовлетворять
функция частицы, имеющей только кинетическую энергию.
Можно также показать, что для частицы, двигающейся по окружности с постоянной скоростью и имеющей только кинетическую энергию поступательного движения (т.е. без учёта энергии покоя частицы) из соотношений (6), (7) и (8) следует второй постулат Бора (правило квантования орбит). Действительно, учитывая, что запишем уравнение (8), следующее из (6) и (7), в виде
Поскольку частица движется по окружности, то отношение определяет время, за которое частица пройдёт расстояние вдоль её траектории равное
. Известно , что при движении частицы по замкнутой траектории действие находится за время одного периода колебания, поэтому отношение
в (13) равно периоду одного полного колебания частицы при величине действия
. Так как, согласно представлениям, изложенным в данной статье, величина действия
может принимать только значения кратные
(квантование действия), то умножим обе части уравнения (13) на целое число
В (14) действию , согласно , соответствует период колебания частицы
, где
– длина окружности траектории частицы.
Поэтому представим (14) в виде
В (15) и (16) – радиус окружности траектории частицы при каком-либо значении числа
.
Соотношение (16) в применении к атому водорода модели Бора позволяет получить правильные значения энергии уровней электронов без использования понятия энергии покоя частицы. В атоме Бора электрон не является свободной частицей, но его полная энергия, равная сумме кинетической энергии электрона и потенциальной энергии электростатического поля ядра атома, по модулю равна кинетической энергии электрона при его движении вокруг ядра и по своей природе она есть бескомпонентная энергия электростатического поля ядра атома, поэтому ей может быть сопоставлена плоская бескомпонентная волна де Бройля с коэффициентом пропорциональности между частотой волны и полной энергией электрона равным .
Следует отметить, что устойчивость квантованных круговых орбит в приведённом выше способе получения правила квантования орбит является следствием квантования действия и не является следствием образования в плоскости орбиты электрона на его траектории стоячих волн де Бройля, поэтому даже если волна де Бройля является одиночной круговые квантованные орбиты частицы будут устойчивыми.
Также в только с учётом кинетической энергии электрона (без учёта энергии покоя) получены значения энергетических уровней круговых орбит электронов в магнитном поле, хорошо согласующиеся с экспериментальными данными.
3. Корпускулярно – волновой дуализм материи при рассмотрении свободной частицы с учётом энергии покоя
Запишем в релятивистской форме соотношение, определяющее корпускулярно-волновой дуализм материи для энергии согласно , в виде , понимая под энергией
полную энергию частицы
:
где – скорость поступательного движения частицы в ИСО, связанной с физическим вакуумом.
Так как
то (17) запишем в виде
Известно, что фазовая скорость волны де Бройля при движении частицы в вакууме определяется соотношением
где – релятивистский импульс частицы.
После подстановки (20) в (19) получим
Из (21) найдём длину волны де Бройля в рассматриваемом случае
Важно отметить, что формула (22) получена с использованием релятивистского понятия полной энергии , в которую входит и энергия покоя частицы
, т.е.
Очевидно, что при формула (22), так же как и формула (12), переходит в формулу де Бройля (9).
В современной квантовой физике часто используется релятивистская формула
Формулы (22) и (24) могут быть преобразованы одна в другую и поэтому дают одну и ту же длину волны частицы.
Следует отметить, что при разложении члена в знаменателе формулы (12) в ряд Тейлора(точнее, в ряд Маклорена) и учёте только двух первых членов ряда формула (12) переходит в формулу (22), поэтому формула (22) является приближённой по отношению к формуле (12).
Рассмотрим теперь уравнение (19). При уравнение (19), следующее из (17), преобразуется к виду
Но при формулы (20) и (22) не имеют математического, а, следовательно, и физического смысла (так как деление на нуль в математике запрещено), поэтому при
и уравнение (25) не имеет физического смысла. Кроме того, в настоящее время отсутствуют и экспериментальные доказательства существования у частиц волновых свойств в случае их покоя в системе отсчёта, связанной с планетой Земля. Таким образом, из уравнений (19) и (25) следует, что, несмотря на учёт в уравнении (21) энергии покоя частицы, волновые свойства появляются у частиц только с началом их движения в ИСО.
Необходимо также отметить, что при выводе формулы (22) используется значение фазовой скорости сопоставляемой частице волны, превышающее скорость света в вакууме
, т.е. очевидным образом скорость частицы
не совпадает со скоростью
. Неравенство
сохраняется и даже значительно усиливается, согласно формуле (20), при
. При учёте энергии покоя частицы в соотношении
, определяющем корпускулярно-волновой дуализм материи для энергии согласно , , приходится принять такое странное физическое явление, как фазовая скорость частицы
, существование которой не имеет смысла при покое частицы в ИСО (согласно соотношениям (20), (22) и (25)), но при появлении у частицы бесконечно малой скорости поступательного движения в ИСО скорость
мгновенно становится больше скорости света в вакууме
и поэтому является принципиально ненаблюдаемой физической величиной.
Представление о том, что при уравнения (17) и (19) переходят в уравнение (8), не соответствует действительности. При
полная энергия частицы
в уравнениях (17) и (19) преобразуется к виду
Из (26) очевидным образом следует, что при
не переходит в
, поэтому и фазовая скорость
волн де Бройля по-прежнему определяется соотношением (20). Действительно, запишем соотношение (20) и преобразуем его для случая
:
Таким образом, формула (20) не переходит при в формулу (10). Эти формулы существуют независимо друг от друга и противоречат друг другу. При этом линейная частота волн де Бройля
при
, согласно формуле (10), определяется выражением
а, согласно формуле (20), также при
Противоречие между формулами (28) и (29) при одном и том же условии очевидно.
Следует отметить, что в данном разделе статьи мы используем постоянную , а не постоянную
, для того, чтобы показать существующее в современной квантовой физике теоретическое противоречие, возникающее при скоростях свободных частиц
, между значениями фазовых скоростей
и частот
волн де Бройля свободных частиц в случае учёта их энергии покоя
и в случае, когда их энергия покоя не учитывается. Ещё раз подчеркнём, что, согласно современной научной литературе, фазовая скорость
волн де Бройля при рассмотрении свободной частицы, двигающейся со скоростью
, без учёта её энергии покоя и значении постоянной
определяется по формуле (10) , а при учёте энергии покоя свободной частицы по формуле (20) , но ведь одна и та же свободная частица не может одновременно иметь две совершенно разные фазовые скорости волн де Бройля и две совершенно разные частоты. Следовательно, исходя из основных положений, изложенных выше в данной статье, выход из возникшего противоречия заключается в том, чтобы принять, что волны де Бройля обусловлены не полной энергией частицы
, а только кинетической энергией
при значении связывающего коэффициента между
и
равном
(или при значении связывающего коэффициента между
и
равном
).
4. Возможная физическая сущность волн де Бройля
Итак, использование в соотношении , определяющем, согласно , , корпускулярно-волновой дуализм материи для энергии, полной энергии свободной частицы
(уравнение (17)) или только её кинетической энергии
(уравнения (7), (8)) при значении постоянной
(или
, при записи соотношения
в виде
), приводит к взаимоисключающим значениям фазовых скоростей
и частот
волн де Бройля при
, однако при этом значения длин волн де Бройля
при использовании физических величин
, согласно формуле (22), или
, согласно формуле (9), при
практически совпадают. Правильный ответ на вопрос о том, какую физическую величину
или
и какой связывающий коэффициент
или
в согласии с физической реальностью необходимо использовать в соотношении, определяющем корпускулярно-волновой дуализм материи для энергии, имеет большое значение для понимания физической природы волн де Бройля. При совпадении фазовой скорости волны де Бройля
со скоростью частицы
волну де Бройля допустимо представлять как локализованное возмущение в физическом вакууме, обусловленное кинетической энергией частицы
(согласно уравнению (8)), это возмущение распространяется со скоростью свободной частицы, также как локализованное возмущение, вызванное движением в физическом вакууме частицы – фотона, совпадает со скоростью созданного им электромагнитного возмущения в вакууме.
Иногда высказывается такая точка зрения, что волны де Бройля представляют собой возмущения в физическом вакууме, подобные волнам, возникающим на водной поверхности или в воздухе при движении в этих средах каких-либо тел или же предлагается понимать волны де Бройля как явление электродинамической генерации волн в материальной среде физического вакуума. Следует отметить, что названные гипотезы предполагают отдачу частицами своей кинетической энергии на генерацию волн даже при равномерном и прямолинейном движении частицы, например, нейтрона, что должно приводить к уменьшению кинетической энергии частицы (так как кинетическая энергия уносится волнами в пространство), и, следовательно, должно происходить уменьшение скорости частицы в противоречие закону инерции, утверждающему возможность бесконечно долгого равномерного и прямолинейного движения частицы вещества в пространстве, свободном от действия полей.
В данной статье волна де Бройля понимается, как локализованное возмущение в физическом вакууме, обусловленное её кинетической энергией. Если частица движется в потенциальном поле, тогда это возмущение в вакууме, обусловленное полной механической энергией частицы. Возмущение в вакууме, превышающее классические размеры частицы, не отрывается от частицы в виде волн в физическом вакууме, а принадлежит частице. Если исходить из представления о тождественности корпускулярных и волновых свойств «обыкновенных» частиц и фотонов и полагать, что фотон локализован на длине его волны , то можно допустить, что «обыкновенные» микрочастицы также локализованы на длине волны де Бройля, но поскольку одиночные фотоны обладают волновыми свойствами, то и одиночная волна де Бройля в изложенном в данной статье представлении должна обладать волновыми свойствами, что подтверждается экспериментально.
Поток частиц, расположенных последовательно друг за другом на расстоянии длины волны де Бройля (величина
, по-видимому, характеризует область распространения в направлении движения частицы физического вакуума, деформированного механической энергией частицы), создаёт волну де Бройля с максимумами и минимумами степени деформации структуры физического вакуума. Максимумы степени деформации структуры вакуума совпадают с местом нахождения частицы. Возможно, что именно такие волны и были обнаружены экспериментально в первых опытах по дифракции микрочастиц. В дальнейшем было доказано, что волновыми свойствами обладают и одиночные микрочастицы. Подобно этому и одиночные фотоны обладают волновыми свойствами, а поток частиц — фотонов допустимо понимать как электромагнитную волну , .
5. Приложение к ядерной физике и электронной микроскопии
В связи с возникшим вопросом о том, какую энергию или
и какой связывающий коэффициент
или
необходимо использовать в соотношении, определяющем корпускулярно-волновой дуализм «обыкновенных» свободных частиц (электронов, протонов, нейтронов и т.п.), автором приведён расчёт значений длин волн де Бройля
, выполненный по формуле (12) и по формуле (22), для различных скоростей
движения свободной частицы в данной ИСО. При выводе формулы (12) было использовано понятие только кинетической энергии свободной частицы
и значение связывающего коэффициента
, а при выводе формулы (22) использовалось понятие полной энергии свободной частицы
и значение связывающего коэффициента
. Результаты расчётов сведены в таблицу 1.
Таблица 1 - Сравнение длин волн де Бройля, определённых по формулам (12) и (22)
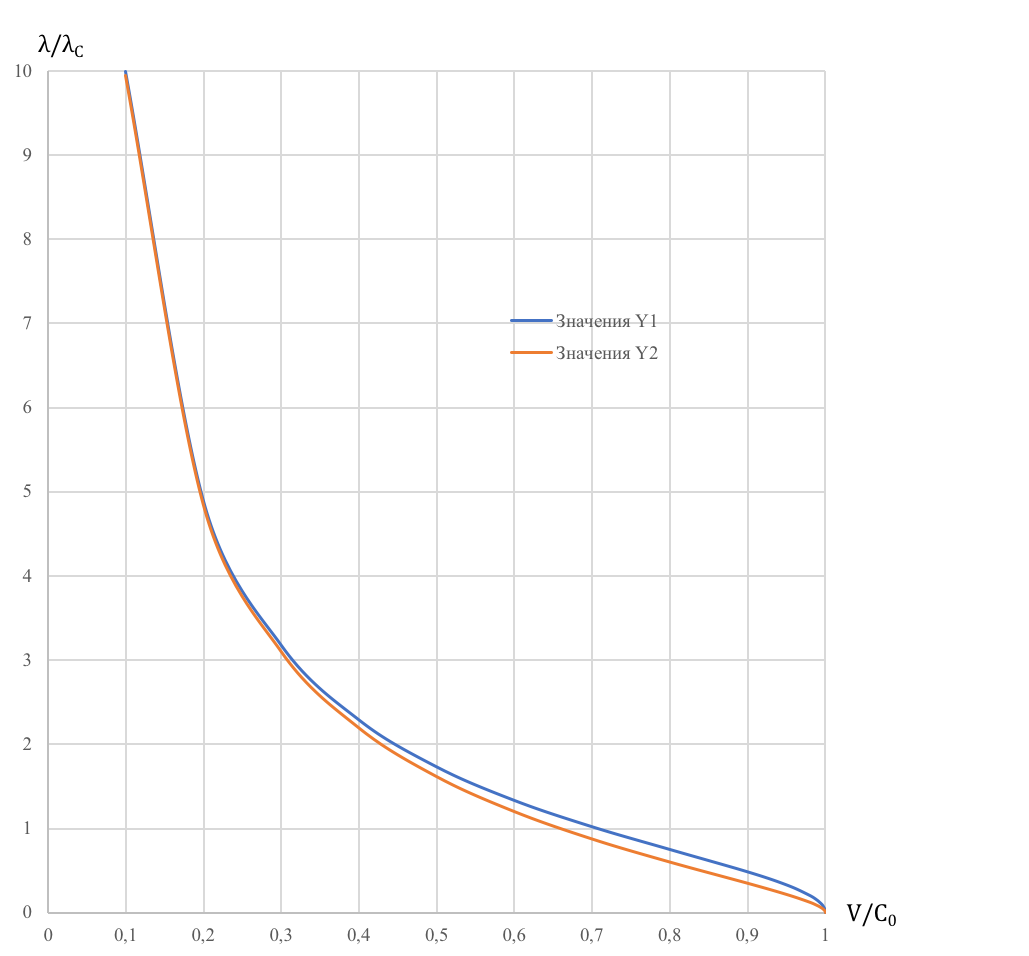
Рисунок 1 - Графики зависимости λ/λC от V/С0 для скоростей движения частицы от 0,1С0 до 0,999999С0
Примечание: λC – комптоновская длина волны частицы, V – скорость частицы, Y1 – значение отношения λ/λC согласно формуле (22), Y2 – значение отношения λ/λC согласно формуле (12)
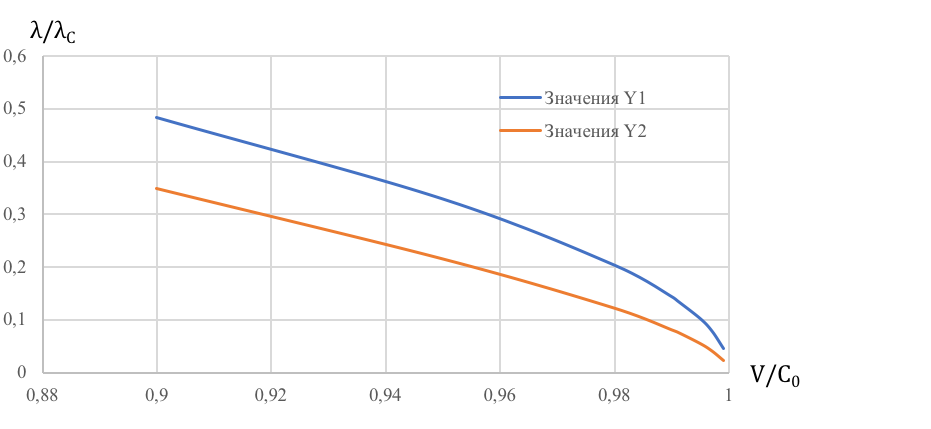
Рисунок 2 - Графики зависимости λ/λC от V/C0 для скоростей движения частицы от 0,9C0 до 0,999C0
Примечание: λC – комптоновская длина волны частицы, V – скорость частицы, Y1 – значение отношения λ/λC согласно формуле (22), Y2 – значение отношения λ/λC согласно формуле (12)
Из анализа данных таблицы 1 и графиков рис. 1 и рис. 2 следует, что, начиная со скорости частицы 0,1C0 и до скорости 0,9999C0, отношение длины волны де Бройля, определённое по формуле (12) к длине волны, определённой по формуле (22), постоянно уменьшается и при скорости 0,9999C0 оно становится очень близким к , при дальнейшем возрастании скорости частицы до её предельно возможного приближения к скорости света это отношение остаётся постоянным и приблизительно равным
. Действительно, при скорости частицы приблизительно равной скорости света
формула (12) может быть преобразована к виду:
Формула (22) при условии преобразуется к виду:
Из сравнения (30) и (31) следует, что при условии формула (12) всегда даёт для частицы в два раза меньшее значение длины волны де Бройля, чем формула (22). Как следует из таблицы 1, условие
выполняется начиная со скорости частицы 0,9999C0.
Заметное изменение отношения длины волны де Бройля, определённое по формуле (12), к длине волны, определённой по формуле (22), в интервале скоростей частиц от 0,5C0 до 0,9999C0 позволяет предложить метод возможного экспериментального подтверждения справедливости формулы (12). В этом случае отношение длины волны, например, к длине волны, например,
, определённых по формуле (12), равно 4,92, а отношение длины волны
к длине волны
, определённых по формуле (22), равно 3,7. Если при скоростях частиц (целесообразно использовать в этом случае протоны) полученных в ускорителе заряженных частиц и равных 0,8C0 и 0,98C0 (соответствующих согласно таблице 1 длинам волн
и
), удастся получить дифракционную картину упругого рассеяния протонов на ядрах с одним и тем же значением радиуса и затем измерить отношение синусов углов дифракционных минимумов, соответствующих скоростям протонов 0,8C0 и 0,98C0, то это отношение должно быть равным или 3,7 или 4,92.
Этот вывод следует из формулы:
где – угол расположения дифракционного минимума на дифракционной картине при каком-либо числе
;
– радиус ядра;
– длина волны де Бройля частицы.
Поэтому
где – синус угла
при скорости частиц 0,8C0;
– синус угла
при скорости частиц 0,98C0.
Значение соотношения близкое к 4,92 будет соответствовать справедливости формулы (12), а значение соотношения
близкое к 3,7 будет соответствовать справедливости формулы (22).
Таким образом, для экспериментальной проверки справедливости формулы (12) согласно предложенному методу достаточно измерить углы при скоростях частиц 0,8C0 и 0,98C0.
В случае экспериментального подтверждения правильности формулы (12) она может оказать значительное влияние на исследования в области ядерной физики и электронной микроскопии.
В современных высокоразрешающих электронных микроскопах ускоряющее электроны напряжение составляет 100 – 400 кВ . Для достижения скорости электронов, например, 0,8C0 значение ускоряющего напряжения в электронном микроскопе должно составлять около 340 кВ, поэтому получение околосветовых скоростей, указанных в таблице 1, в современных электронных микроскопах не представляет принципиальных технологических затруднений. При скорости электронов 0,8C0 длина волны де Бройля, рассчитанная по формуле (22) в 1,25 раза превышает длину волны де Бройля, рассчитанную по формуле (12). Такое отличие в длинах волн де Бройля, рассчитанных по формулам (22) и (12), является достаточно существенным, чтобы оказать влияние на оценку разрешающей способности электронного микроскопа, которая во многом определяется длиной волны потока электронов .
6. Основные результаты
Научная новизна статьи, согласно данным автора, заключается в следующем:
1. Обосновано значение коэффициента, связывающего частоту бескомпонентной монохроматической волны де Бройля с энергией сопоставляемой ей свободной частицы, имеющей только кинетическую энергию, равное . Исходя из значения связывающего коэффициента
обосновано равенство скорости
поступательного движения частицы, имеющей только кинетическую энергию, с фазовой скоростью
волны де Бройля, сопоставляемой данной частице (уравнение (8)). Равенство
ранее было получено в , , однако в настоящей статье указанное равенство при новом подходе с использованием коэффициента
выводится из основной формулы квантовой теории, определяющей энергию фотона,
2. На основании равенства сделано предположение о том, что появление волн де Бройля обусловлено воздействием кинетической энергии свободной частицы (без учёта её энергии покоя) на структуру физического вакуума. Для проверки этого предположения предложена новая релятивистская формула для нахождения длины волны частицы
только при учёте её кинетической энергии (формула (12)).
3. Предложен метод экспериментальной проверки формулы (12) в ядерной физике и показана возможность применения формулы (12) для повышения точности оценки разрешающей способности электронных микроскопов.
7. Заключение
В результате проведённого исследования выдвинута и обоснована гипотеза о том, что физическая природа волн де Бройля обусловлена воздействием кинетической энергии свободной частицы (или механической энергией частицы, двигающейся в потенциальном поле) на структуру физического вакуума. Показана возможность применения новой релятивистской формулы для нахождения длин волн де Бройля в ядерной физике и электронной микроскопии. Наиболее эффективно формула (12) может применяться, как показывают данные таблицы 1 и графики рис. 1 и рис. 2, при скоростях движения частиц от 0,3C0 и до предельно возможного приближения к скорости света.
