МОДЕЛЬ ФЛУКТУАЦИОННОЙ ИЗМЕНЧИВОСТИ НА ПРИМЕРЕ ЛИСТОВЫХ ПЛАСТИН ПШЕНИЦЫ
МОДЕЛЬ ФЛУКТУАЦИОННОЙ ИЗМЕНЧИВОСТИ НА ПРИМЕРЕ ЛИСТОВЫХ ПЛАСТИН ПШЕНИЦЫ
Аннотация
Листовые пластины пшеницы, как и всех злаковых, имеют продольное жилкование, которое создает трудность при изучении флуктуирующей асимметрии (ФА) гомологичных билатерально симметричных структур. Для определения ФА (ненаправленного отклонения от нуля разности между правой и левой структурой) и направленной асимметрии (НА, сдвиг в одну из сторон), был использован метод геометрической морфометрии. Достоинство этого метода в выравнивании координат меток и удалении компонента размера в выборке образцов листовых пластин.
По контуру листа выставлялось 100 меток, равномерно по 50 с каждой стороны и проведено определение величины ФА и НА. Присутствие и значимость направленной асимметрии находилось в двух факторном дисперсионном анализе с помощью фактора «сторона», а ФА – по взаимодействию факторов «лист» и «сторона». Величина флуктуирующей асимметрии определялась по разности дисперсии левых и правых меток. Направленная асимметрия находилась вычитанием среднего значения из разности |L – R|, где L и R – величина дисперсии левой и, соответственно, правой метки.
Было проведено сравнение асимметрии листовых пластин 4-х популяций, выращенных при различных дозах удобрения, от интенсивной дозы минеральных удобрений, до, высокоинтенсивной, включавшей органические (навоз КРС) и минеральные удобрения (аммофос). В качестве испытуемого материала было использовано два сорта пшеницы: один сорт озимой и один – яровой.
Значительное снижение стабильности развития (увеличение ФА) с повышением дозы удобрения получено в растениях озимой пшеницы. Яровая пшеница показала постепенное снижение ФА от первой к четвертой дозе удобрения. Оба вида асимметрии проявляли положительную корреляционную связь: озимая пшеница Spearman’s r = 0,61 и 0,64 – яровая.
Моделирование с помощью регрессионного анализа показало, что отклик (ФА) озимого сорта находился в экспоненциальной зависимости от обоих факторов: от дозы (χ2 = 264,5) и от направленной асимметрии (χ2 = 167,5; везде р << 0,05). Экспоненциальная модель объясняла 81,7% дисперсии остатков.
Для яровой пшеницы получена полиномиальную модель зависимость, которая объясняла 73% дисперсии остатков и показала значимость только фактора направленной асимметрии (χ2 = 14,1; р = 0,0002). В обеих моделях применялось экспоненциальное распределение Твиди. Критерий оценки значимости коэффициентов регрессии Вальда показал результаты подтверждающие результаты оценки критерием кси-квадрат (χ2). Таким образом, в листьях яровая пшеницы флуктуационная изменчивость снижалась по мере увеличения дозы удобрения и показала полиномиальную модель зависимости от направленной асимметрии, по которой повышение дозы снижало асимметричность, в противоположность озимой пшеницы, которая показала стойкое увеличение нестабильности развития и общей асимметрии с повышением дозы вносимого удобрения.
1. Введение
Флуктуационная изменчивость – это колебание величины морфологических, биохимических, а также других показателей около среднего значения, генетически обусловленного нормой реакции.
Существует несколько гипотез объясняющих природу флуктуационной изменчивости. В листовых пластинах, в том числе злаковых растений, ее определяют по величине флуктуирующей асимметрии (ФА) левых и правых гомологичных признаков, например по ширине листовой пластины или любых других счетных или мерных билатерально симметричных структур.
Под термином «стабильность развития» понимается биохимический статус организма с определенным уровнем ФА. Известно, что у древесных растений высокое отклонение величины ФА в сравнении с контролем означает снижение стабильности развития популяции , .
Направленная асимметрия – это направленный сдвиг разности между левыми и правыми величинами в одну из сторон, левую или правую, которая часто встречается в растениях из-за фототаксиса – синтеза клеток по направлению к источнику освещения и регулируется фитогормонами в меристеме. В отличие от ФА, направленная асимметрия наследуема и теснее связана с генотипом.
Для злаковых характерны оба вида асимметрии. Так в проведенных ранее исследованиях замечено, что в листьях пшеницы, ржи, ячменя и овса в 80% случаях встречались оба вида асимметрии в равном или неравном соотношении , . На долю того или иного вида асимметрии оказывали влияния климатические условия года, доза вносимого удобрения и способ обработки почвы .
Наиболее точно индекс ФА находят в смешанном 2-х факторном дисперсионном анализе (лист × сторона) с вычетом ошибки измерения, где фактор «лист» является рандомным фактором, а «сторона» – фиксированным.
Метод геометрической морфометрии позволяет с использованием программных средств (TPSDig2, MorphoJ) искусственно увеличить число признаков в виде равномерно расставляемых меток по краю правой и левой половины листа .
Консенусная фигура пластины строится с учётом расположения всех меток, дисперсии ХУ координат меток и обеспечивает определение ФА и НА по совокупности наносимых меток. Соотношение ФА/НА указывает на соотношение фенотипического и генотипического компонентов асимметрии, а доля ФА указывает на изменчивость стабильности развития .
Наиболее удобным для изучения фактором, влияющим на асимметрию билатеральных признаков злаковых, представляется доза удобрения, вносимого под зерновую культуру, т.к. питательные вещества стимулируют рост вегетативных и генеративных органов растения и повышают конечную биологическую продукцию зерна в колосе.
Целью работы было построить модель изменения стабильности развития в виде величины ФА в зависимости от направленной асимметрии и с учетом дозы вносимого удобрения. Для сравнения использовалось два распространенных сорта пшеницы, один сорт озимой и один – яровой.
2. Методы и принципы исследования
2.1. Места сбора
Флаговые листовые пластины пшеницы (Triticum aestivum L.,1753), прилегающие к колосу, собирались во второй половине июля 2019 г. (озимая, сорт Поэма) и в 2020 г. (яровая, сорт Грань) на территории Федерального Аграрного Научного центра (г. Суздаль, Владимирская обл.), где на серых лесных почвах Суздальского Ополья проводится многолетний адаптивно-ландшафтный эксперимент с разработанной системой севооборота и внесения удобрения.
Использовалось 4 дозы минерального удобрения нитроаммофоска (NPK). По принятой технологии были внесены следующие дозы:
1) интенсивная (N90P90K90);
2) высокоинтенсивная (N120P120K120);
3) интенсивная органоминеральная (60 т органического удобрения + N90P90K90);
4) высокоинтенсивная органоминеральная (80 т органического удобрения + N120P120K120).
Все дозы вносились непосредственно перед посевом.
Площадь участка составляла 35 м2 (5×7), а контролем служили полосы шириной 1 м, разделявшие делянки с различными дозами удобрения. Листовые пластины собирались рандомно, избегая края делянки 1 м шириной. Отбирались пластины с длиной 16-18 см, затем выбирались симметричные пластины без изгибов и поражения микроорганизмами.
Таким образом, с каждой делянки (всего четыре) было отобрано 25-30 пластин. Сначала они вымачивались сутки в бытовом 5%-м детергенте, затем высушивались и наклеивались на бумагу нижней стороной наверх и сканировались с помощью сканера Canon MF3010 (dpi 300) вместе с мерной линейкой, градуированной по ГОСТ. Изображения сохранялись в формате JPG.
2.2. Статистическая обработка и моделирование
Основные статистики выборок |L – R| определялись в программе STATISTICA10 (StatSoft Ink, 2011). Нанесение основных меток (true landmarks, программа TPSDig2) проводилось в точку основания пластины, лишенной лигулы (язычка) и на верхушку пластины (апекс). Вспомогательные метки (semilandmarks) наносились с равным интервалом по каждой стороне листа по 50 меток.
С помощью программы MorphoJ (Klingenberg, 2019) проводилось усреднение и выравнивание всех контуров листовых пластин, таким образом, создавалась консенсусная форма и по дисперсии координат меток (суммы квадратов координат Х и У) рассчитывалась дисперсия каждой правой и левой метки (программа TPSRelw). По разности дисперсии рассчитывалась флуктуирующая асимметрия. Значимость ФА тестировалась в 2-х факторном дисперсионном анализе по эффекту взаимодействия факторов «лист» и «сторона». Присутствие направленной асимметрии определялось по значимости эффекта фактора «сторона». Выборка, содержащая ФА не содержала примесь НА, т.к. из разности L – R по абсолютной величине вычиталось среднее значение. Полученное значение и служило величиной направленной асимметрии.
Для проверки на присутствие антисимметрии была проведена визуальная проверка на выбросы, а также находился коэффициент корреляции Спирмена на отрицательную связь между значениями левого и правого признаков в выборках.
Для построения модели ФА – НА – доза удобрения был использован метод регрессионного анализа. Он был удобен в том, что позволял оценить влияние двух факторов (НА и величины дозы удобрения) на результирующий отклик, в нашем случае индекс флуктуирующей асимметрии.
3. Основные результаты
3.1. Описательная статистика
Все выборки |L – R| (L – дисперсия левой метки; R – дисперсия правой метки) обладали непараметрическим распределением (К-С тест р < 0,05) из-за высокой дисперсии у верхушки и основания листа и в большинстве случае содержали примесь направленной асимметрии, но большую долю асимметрии занимала флуктуирующая асимметрия.
Не было получено отрицательной корреляции между L и R, т.е. антисимметрия отсутствовала. Предварительно был проведен факторный дисперсионный анализ по влиянию дозы и направленной асимметрии на ФА двух сортов пшеницы. Значимыми был фактор дозы (df = 3; F = 7,5; p << 0,05), который влиял на ФА в зависимости от сорта (df = 1; F = 5,24; p < 0,05). 4-я доза способствовала повышению индекса ФА озимой пшеницы. Этот сорт показал высокую корреляцию ФА/НА в сгруппированных данных (Рисунок 1).
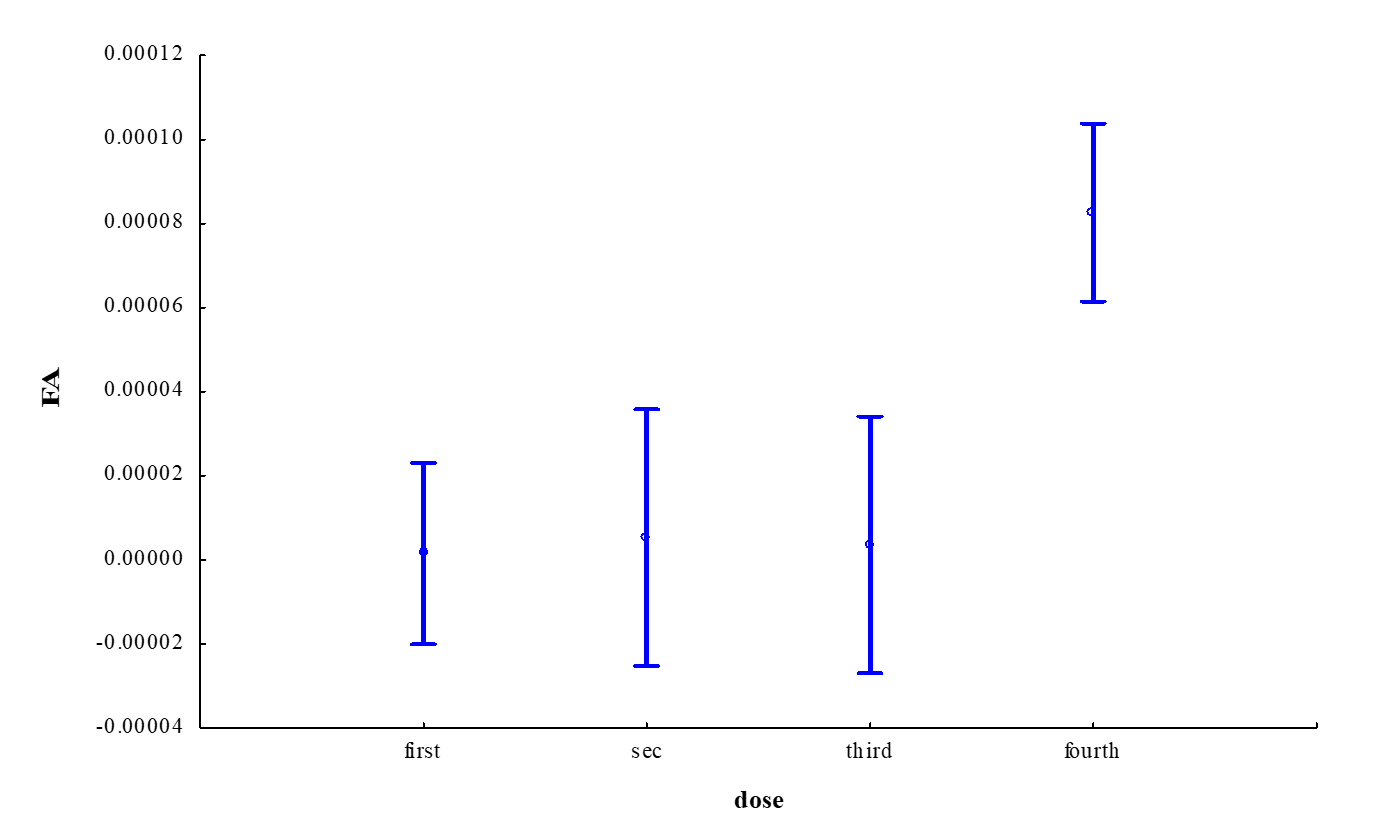
Рисунок 1 - Результаты однофакторного дисперсионного анализа по влиянию дозы удобрения на флуктуирующую асимметрию листьев озимой пшеницы (F(3; 148) = 12,16; p << 0,05)
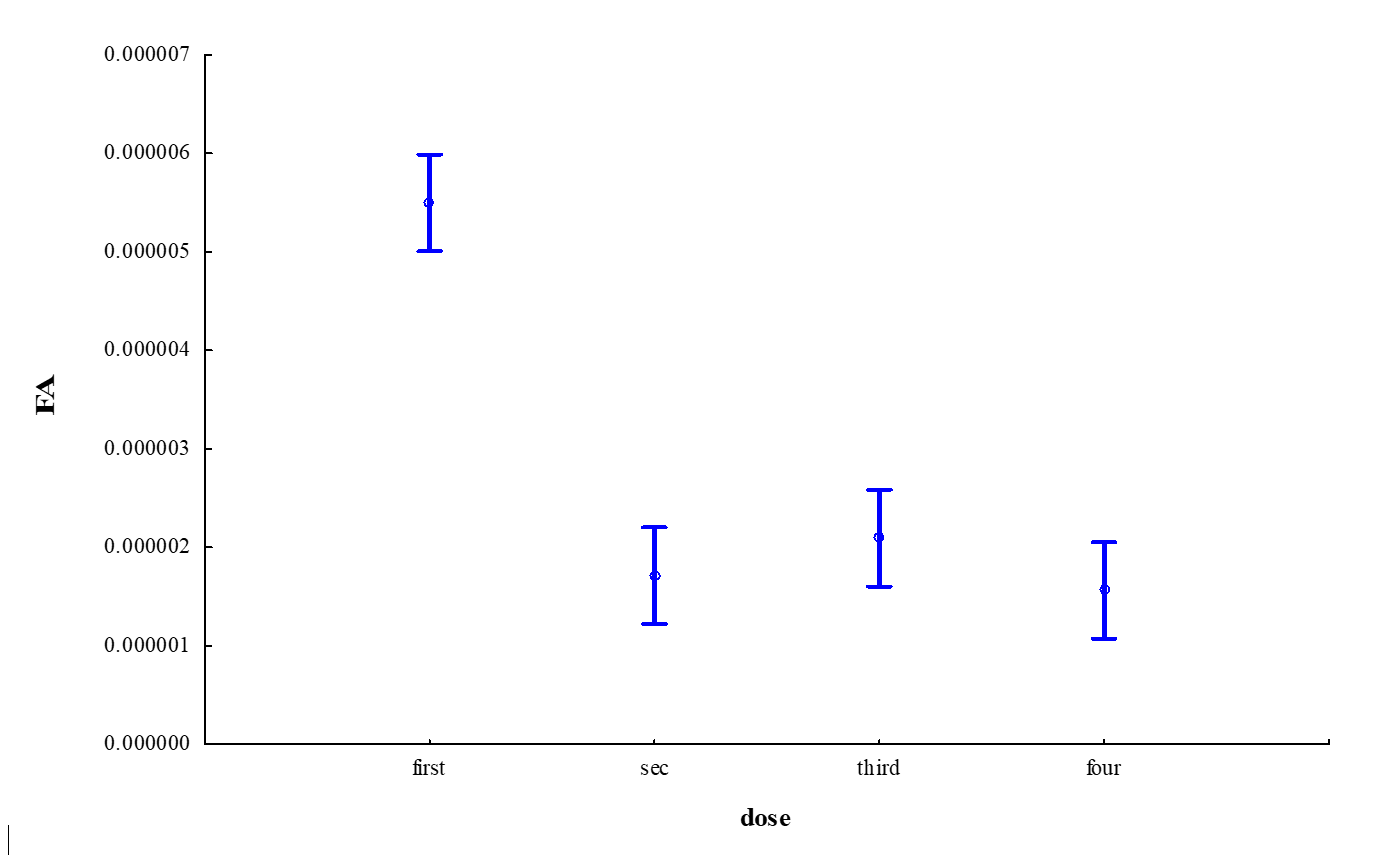
Рисунок 2 - Влияние дозы удобрения на флуктуирующую асимметрию листьев яровой пшеницы (F(3; 96) = 57; p << 0,05)
3.2. Моделирование
Озимая пшеница. В качестве категориальной переменной была выбрана доза вносимого удобрения (от 1-й до 4-й). Числовой переменной служили значения направленной асимметрии для каждой метки (всего 100 меток). Зависимой переменной служили значения ФА.
Был построен гнездовой план без взаимодействия эффектов, и использовалась опция «обобщенная линейная модель» (GLM, STATISTICA), позволяющая объединить различные модели распределения. Наиболее подходящая модель оказалась модель Твиди (TWEEDIE), относящаяся к экспоненциальному семейству моделей, связывающих дисперсию и среднее степенное. Была использована логарифмическая функция связи (link function). Регрессия ФА/НА показала близкие линии тренда, повышающиеся к 4-й дозе (ось ОХ; Рисунок 3).
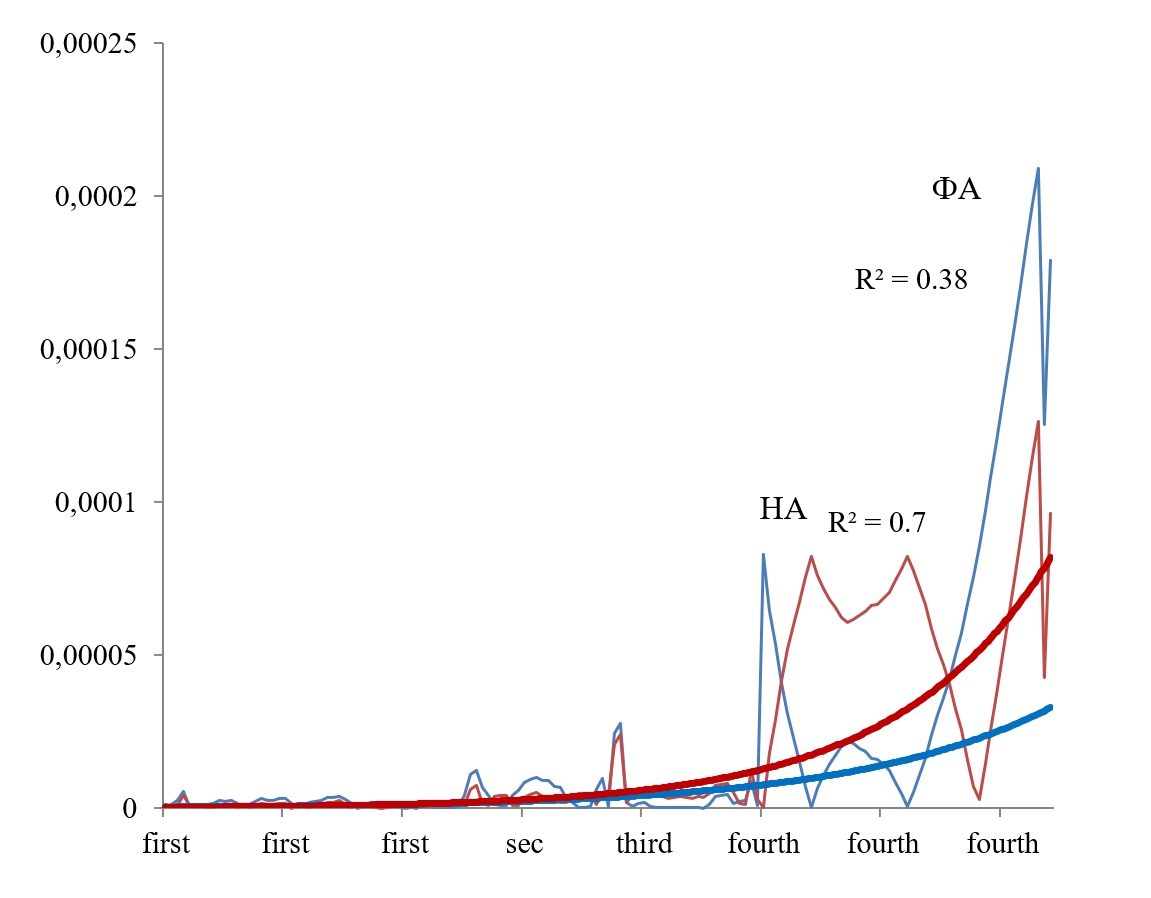
Рисунок 3 - Аппроксимационные линии тренда ФА (синяя линия) и НА (красная)
Примечание: Озимая пшеница, сорт Поэма, Excel
Яровая пшеница. Наиболее точная модель показала полиномиальное распределение оп фактору направленной асимметрии. Чем больше степень, тем выше была степень детерминации модели (на графике - пятая степень).
Полиномиальная регрессия статистически была значима только по R, но не по R2, например, фактор дозы был незначим (р > 0,05).
Общая регрессионная модель показывала высокую значимость R = 0,86. Был также применен тест Вальда (Wald) с нулевой гипотезой о равенстве нулю коэффициентов регрессии. Этот тест является асимптотическим, т.е. предназначенным для описания предельного поведения функций. Распределение Твиди показывало значимость только фактора направленной асимметрии – 15,7 р << 0,05), в целом модель была адекватной относительно направленной асимметрии (Рисунок 4).

Рисунок 4 - Аппроксимационные линии тренда ФА (синяя линия) и НА (красная)
Примечание: Яровая пшеница, сорт Грань, Excel
Другие виды распределения, например, логарифмическое нормальное, не подтверждали значимость коэффициентов регрессии, или подтверждали один из них, например по фактору дозы, на уровне 1-й, 2-й дозы.
Построенные линейные тренды свидетельствовали о различии двух сортов пшеницы в морфологии листовых пластин. У озимой пшеницы они были оформлены полностью как полноценный фотосинтезирующий орган растения, а время вегетации яровой было на два месяца короче, следовательно, ФА варьировала не так сильно, как в сорте озимой (Поэма).
4. Заключение
Стабильность развития была пониженной у озимой пшеницы (более высокая ФА) особенно, при четвертой высокоинтенсивной органоминеральной дозе. Мы считаем, что разные сроки вегетации (более короткая у яровой пшеницы) играют роль в стабильности развития. Отсюда – различные допустимые модели описывающие влияние генотипически зависимой направленной асимметрии и дозы удобрения на стабильность развития. Экспоненциальная модель была характерна для озимой. Полиномиальная, далекая от линейной – для яровой пшеницы. Авторы полагают, что моделирование стабильности развития представляет интерес при учете других факторов, климатических, а также факторов обработки почвы.
При разработке системы моделирования следует учитывать множество экспериментальных данных для получения системы, состоящей из набора модулей, например, использовать разработанные и описанные модели базовых процессов в специализированных программах .
Интерес представляет моделирование биометрических показателей в зависимости от сорта и влажности семян . При этом важно принимать во внимание модели флуктуаций не только асимметричности пластин, но и продуктивных показателей устойчивости агроэкосистем, как толерантности агроценоза к факторам среды .
