ON MODELING LONG-TERM MACROECONOMIC GROWTH
О МОДЕЛИРОВАНИИ ДОЛГОСРОЧНОГО МАКРОЭКОНОМИЧЕСКОГО РОСТА
Научная статья
Михайловская военная артиллерийская академия, Санкт-Петербург, Россия
* Корреспондирующий автор (azvyagintsev[at]mail.ru)
АннотацияСтатья посвящена вопросам моделирования краткосрочных циклов и долгосрочных трендов, наблюдаемых в экономике. Особое внимание уделяется проблеме стабилизации рыночных колебаний, при этом исследуется не природа краткосрочных волн, а возможность управления их динамикой. В статье представлена экономико-математическая модель в виде нелинейной дискретной системы третьего порядка, которая позволяет имитировать и анализировать возможные сценарии экономического развития с учетом циклических колебаний. При разработке этой модели были использованы математические методы современной теории управления хаосом. С помощью полученной модели на основе реальных статистических данных построен долгосрочный макроэкономический прогноз для Китая. Научная и практическая ценность этой модели заключается в том, что она дает возможность определять точные сроки и затраты, необходимые для стабилизации циклических процессов в экономике.
Ключевые слова: макроэкономический тренд, циклические колебания, математическое моделирование, стабилизация.
ON MODELING LONG-TERM MACROECONOMIC GROWTH
Research article
Zvyagintsev A.I.*
Mikhailovskaya Military Artillery Academy, St. Petersburg, Russia
* Corresponding author (azvyagintsev[at]mail.ru)
AbstractThe article discusses the modeling of short-term cycles and long-term trends observed in the economy. Particular attention is paid to the problem of stabilization of market fluctuations while investigating the possibility of controlling the dynamics of short-term waves instead of their nature . The article presents an economic and mathematical model in the form of a nonlinear discrete system of the third order, which allows simulating and analyzing possible scenarios of economic development taking into account cyclical fluctuations. When developing this model, the research implemented mathematical methods of modern chaos control theory were used. With the help of the obtained model, the study outlines a long-term macroeconomic forecast for China is on the basis of real statistical data. The scientific and practical value of this model lies in the fact that it makes it possible to determine the exact terms and costs necessary to stabilize cyclical processes in the economy.
Keywords: macroeconomic trend, cyclical fluctuations, mathematical modeling, stabilization.
Введение
В процессе экономического развития любой страны важное значение имеет анализ долгосрочных тенденций, а также управление краткосрочными колебаниями, поскольку такие флуктуации могут приводить к серьезным отклонениям от оптимального тренда, что негативно отражается на состоянии экономики. В данной работе рассматриваются задачи моделирования как долгосрочных трендов, так и краткосрочных циклов. Особое внимание уделяется проблеме стабилизации рыночных колебаний, при этом нас будет интересовать не природа краткосрочных волн, а управление их динамикой.
Усовершенствование известных и разработка новых методов прогнозирования в экономике по-прежнему сохраняют высокую актуальность. Вопросам математического моделирования глобальной, региональной и национальной динамики с учетом воздействия циклических колебаний посвящено огромное количество научных трудов. В работе [1] дан обширный обзор современных методов и моделей долгосрочного прогнозирования, указаны направления их усовершенствования, изложена методология циклического прогнозирования.
Методы и принципы исследования
В работах А.А. Акаева [2], [3, С.46] предложена экономико-математическая модель циклических колебаний деловой активности вокруг трендовой кривой макроэкономического роста
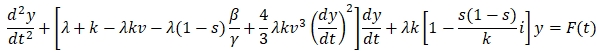 (1)
(1)
Здесь ![]() - текущий объем выпуска продукции (текущий уровень ВВП),
- текущий объем выпуска продукции (текущий уровень ВВП), ![]() - уровень выпуска, соответствующего трендовой траектории долгосрочного экономического роста. Нелинейное дифференциальное уравнение (1) содержит параметры: λ - скорость реакции запаздывания предложения от спроса, k - скорость реакции запаздывания фактических индуцированных капиталовложений от решения об инвестициях, v - мощность акселератора, s - коэффициент сбережений, β - эластичность выпуска по труду, γ - параметр Оукена, i - норма процента. Функция
- уровень выпуска, соответствующего трендовой траектории долгосрочного экономического роста. Нелинейное дифференциальное уравнение (1) содержит параметры: λ - скорость реакции запаздывания предложения от спроса, k - скорость реакции запаздывания фактических индуцированных капиталовложений от решения об инвестициях, v - мощность акселератора, s - коэффициент сбережений, β - эластичность выпуска по труду, γ - параметр Оукена, i - норма процента. Функция ![]() в правой части уравнения (1) характеризуется цикличностью и определяется формулой
в правой части уравнения (1) характеризуется цикличностью и определяется формулой
где ![]() - независимые автономные инвестиции,
- независимые автономные инвестиции, ![]() - трендовая траектория инвестиций. Таким образом, φ является квазипериодической функцией, колеблющейся вокруг трендовой составляющей.
- трендовая траектория инвестиций. Таким образом, φ является квазипериодической функцией, колеблющейся вокруг трендовой составляющей.
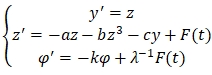 (3)
(3)
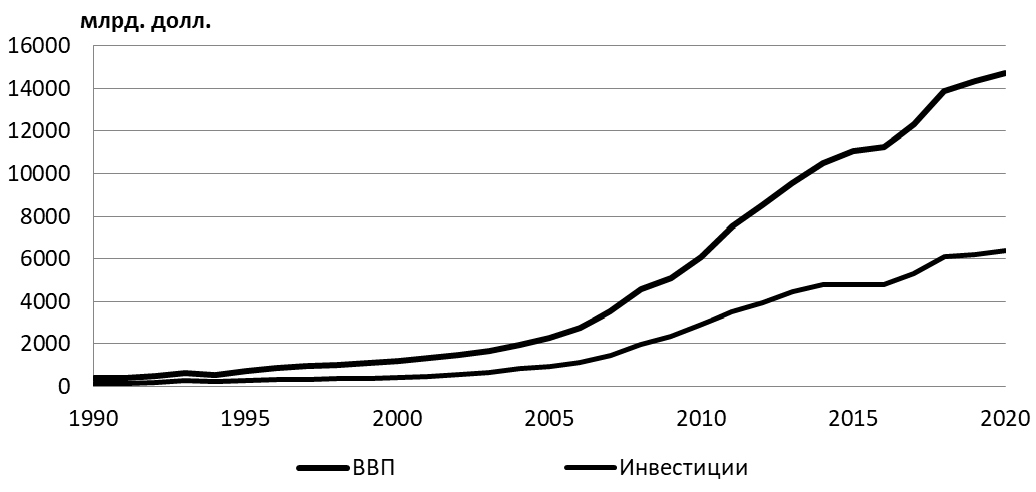
В качестве примера рассмотрим 30-летнюю выборку из статистических данных по ВВП и инвестициям для Китая [4], [5], экономика которого в настоящее время является авангардной на мировой арене.
Рис. 1 – ВВП и инвестиции Китая
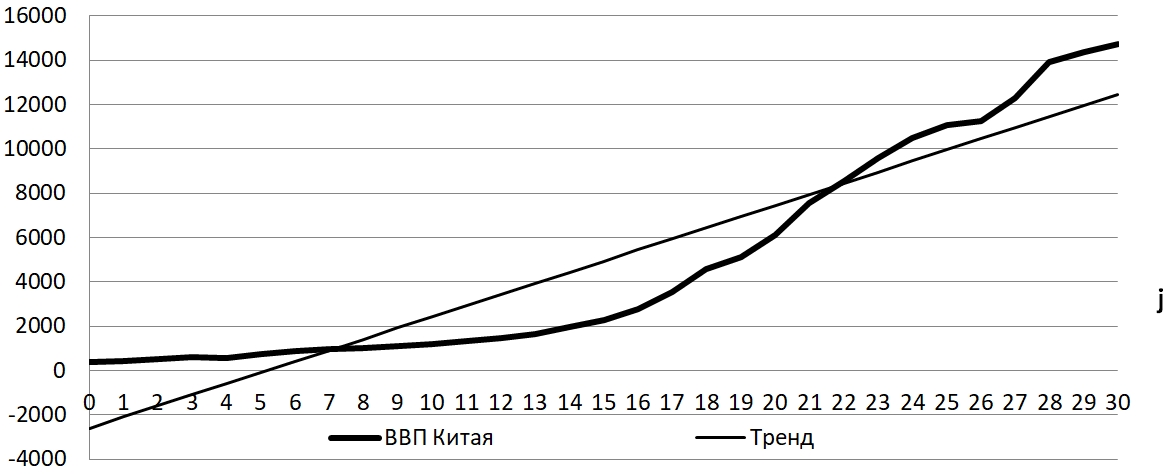
С помощью метода наименьших квадратов находятся линейные тренды, которые для ВВП и для инвестиций соответственно имеют вид:
![]() (4)
(4)
Рис. 2 – ВВП Китая и тренд
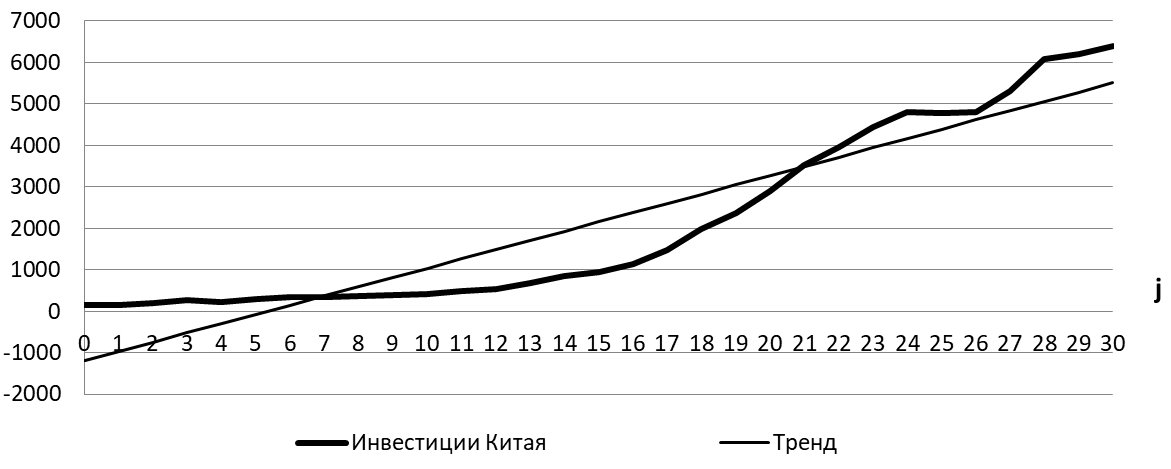
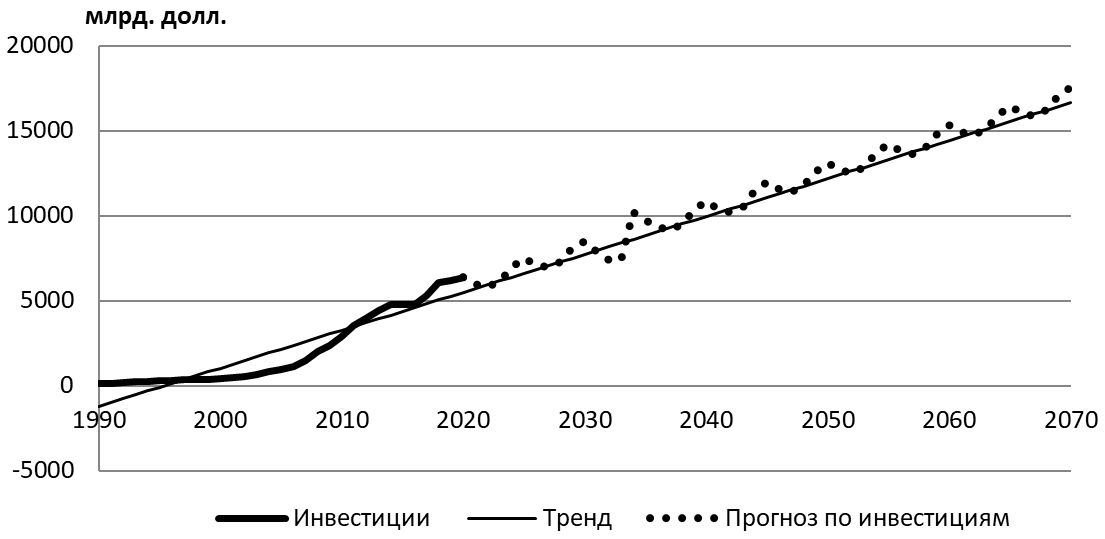
Рис. 3 – Инвестиции Китая и тренд
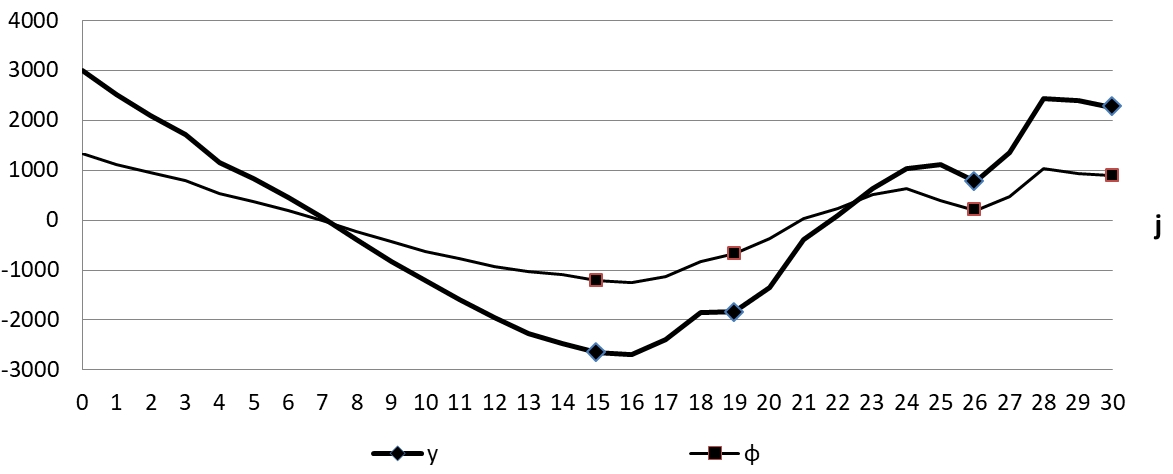
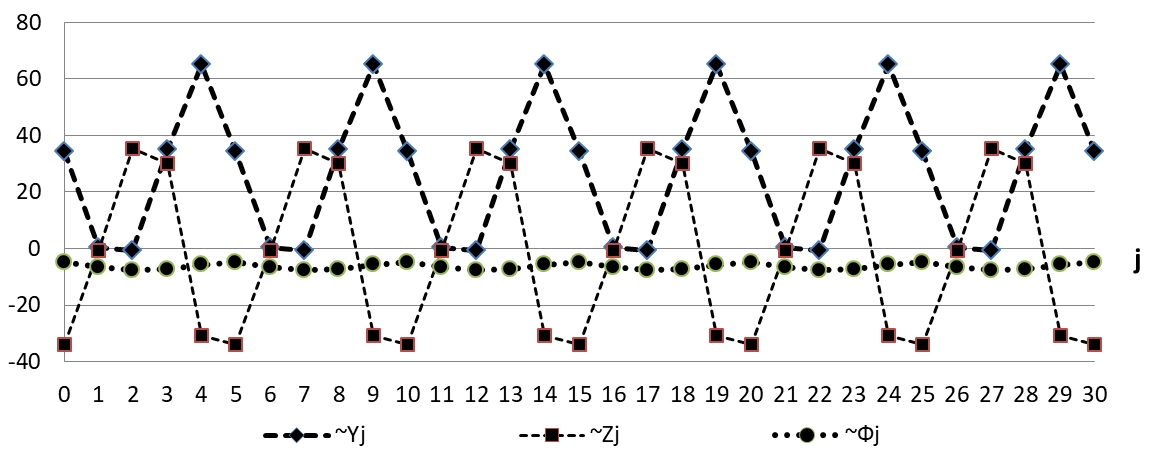
На рисунке 4 представлены графики для ![]() . С одной стороны, поведение этих графиков довольно хаотично. А с другой стороны, в последние 15 лет у траекторий y и φ можно выделить по 3 волны, у которых схожая конфигурация, но различные амплитуды и периоды. На рисунке 4 начало и конец для каждой волны обозначены маркером. Таким образом, можно констатировать, что траектории y и φ имеют квазипериодическую форму. Поскольку на 15-летнем интервале наблюдаются 3 волны, то последнее время у квазипериодических траекторий y и φ период в среднем составляет 5 лет.
. С одной стороны, поведение этих графиков довольно хаотично. А с другой стороны, в последние 15 лет у траекторий y и φ можно выделить по 3 волны, у которых схожая конфигурация, но различные амплитуды и периоды. На рисунке 4 начало и конец для каждой волны обозначены маркером. Таким образом, можно констатировать, что траектории y и φ имеют квазипериодическую форму. Поскольку на 15-летнем интервале наблюдаются 3 волны, то последнее время у квазипериодических траекторий y и φ период в среднем составляет 5 лет.
Рис. 4 – Квазипериодические траектории y и φ
В целях моделирования долговременных прогнозов по ВВП и инвестициям будем рассматривать систему (3) в качестве исходной. Прогнозирование в экономике имеет важное значение. Но мы рассмотрим более интересную с практической точки зрения задачу: возможно ли в реальности обеспечить спрогнозированное развитие экономики и какими должны быть управленческие действия для обеспечения такого развития?
Поскольку мы оперируем дискретными значениями макроэкономической статистики, то для моделирования целесообразно перейти от дифференциальных уравнений к разностным уравнениям. Тогда экономико-математическая модель (3) преобразуется в дискретную систему уравнений
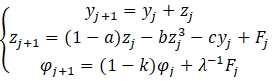 (5)
(5)
Для значений ![]() коэффициент корреляции составляет 0,99, то есть между ВВП и инвестициями наблюдается очень высокая взаимосвязь. Поскольку ВВП и инвестиции взаимно зависимы, то будем рассматривать модель следующего вида:
коэффициент корреляции составляет 0,99, то есть между ВВП и инвестициями наблюдается очень высокая взаимосвязь. Поскольку ВВП и инвестиции взаимно зависимы, то будем рассматривать модель следующего вида:
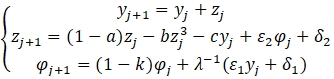 (6)
(6)
Покажем, что использование дискретной системы (6) позволяет осуществлять моделирование циклических процессов в экономике. Из вышеизложенного следует, что интерес представляют циклы с периодом 5 лет. В результате компьютерного эксперимента были подобраны численные значения параметров системы (6):

Необходимо отметить, что для нахождения этого 5-цикла потребовалось вычислить все его координаты с точностью до 14-го знака после запятой, поскольку решения системы (6) очень чувствительны к изменениям коэффициентов и начальных данных.
Графики найденного периодического решения дискретной системы (6) представлены на рисунке 5.
Рис. 5 – Периодическое решение системы (6)
Поскольку для квазипериодических траекторий ![]() характерна хаотичность, то в целях преодоления хаотичной динамики осуществим модификацию модели (6), используя результаты из современной теории управления хаосом.
характерна хаотичность, то в целях преодоления хаотичной динамики осуществим модификацию модели (6), используя результаты из современной теории управления хаосом.
Основные результаты
Введем обозначения
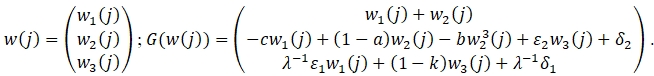 Для вектор-функции G матрица Якоби имеет следующий вид:
Для вектор-функции G матрица Якоби имеет следующий вид:
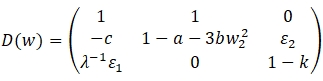
Совершив линеаризацию системы (7) в окрестности найденного 5-цикла с координатами ![]() , а затем применив метод Пирагаса [6], получим модифицированную систему:
, а затем применив метод Пирагаса [6], получим модифицированную систему:
где U(j) является функцией управления, предназначенной для стабилизации поведения решений системы. Используя результаты работ [7] и [8] по стабилизации дискретных систем, получили функцию управления следующего вида:
Дискретная система (8) характеризуется сверхвысокой чувствительностью к изменениям начальных условий. Даже незначительные изменения начальных данных влекут существенные перемены в поведении решений. Таким образом, за счет вариации начальных условий модель (8) способна имитировать различные сценарии, которые вполне соответствуют реальным макроэкономическим процессам.
В целях моделирования долгосрочного прогноза для циклических колебаний деловой активности вокруг трендовой кривой найдем решение системы (8) с начальными условиями
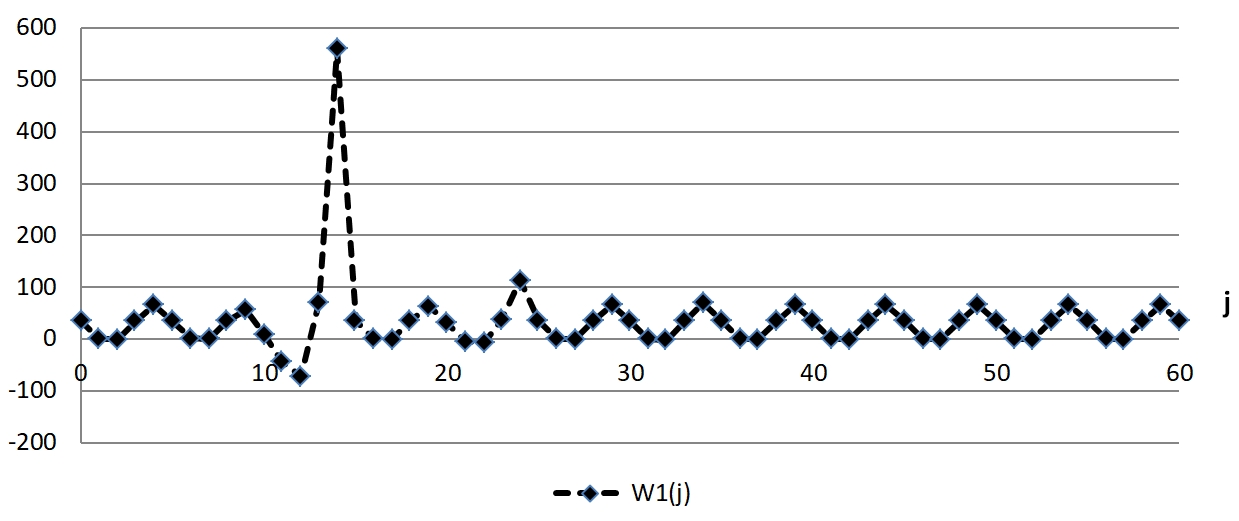
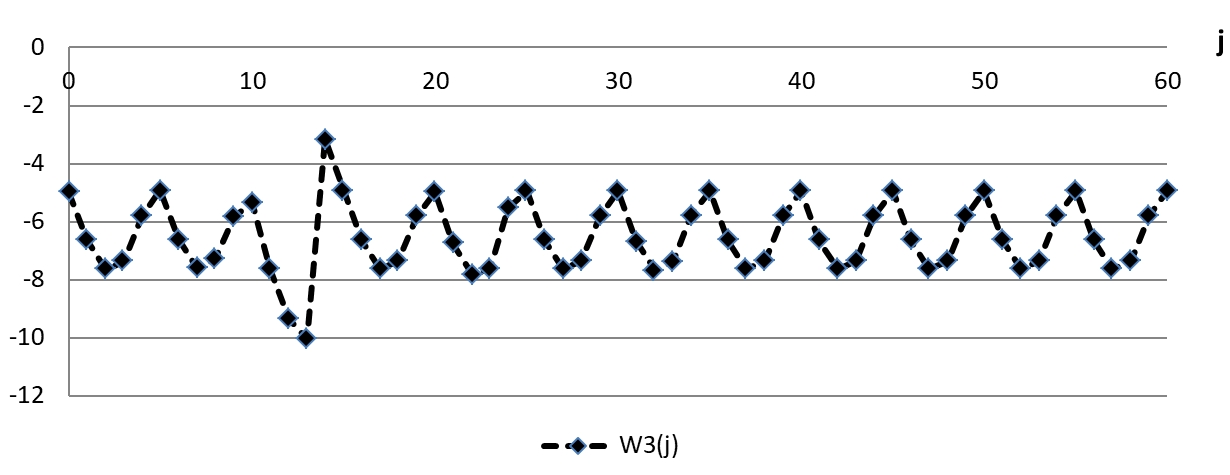
Графики решения системы (8) с начальными условиями (10) представлены на рисунках 6 и 7, из которых видно, что в первой половине 60-летнего периода эти графики характеризуются хаотичностью (аналогично квазипериодическим траекториям y и φ), а во второй половине наблюдаются устойчивые колебания с постоянной амплитудой.
Рис. 6 – График решения ![]() системы (8)
системы (8)
Рис. 7 – График решения ![]() системы (8)
системы (8)
Таким образом, сконструированная система (8) дополнительно дает очень важную возможность моделировать процесс стабилизации, в результате которой формируется устойчивый долгосрочный циклический режим. Преодоление хаотичной динамики и формирование устойчивой периодической траектории достигается за счет функции управления (9).
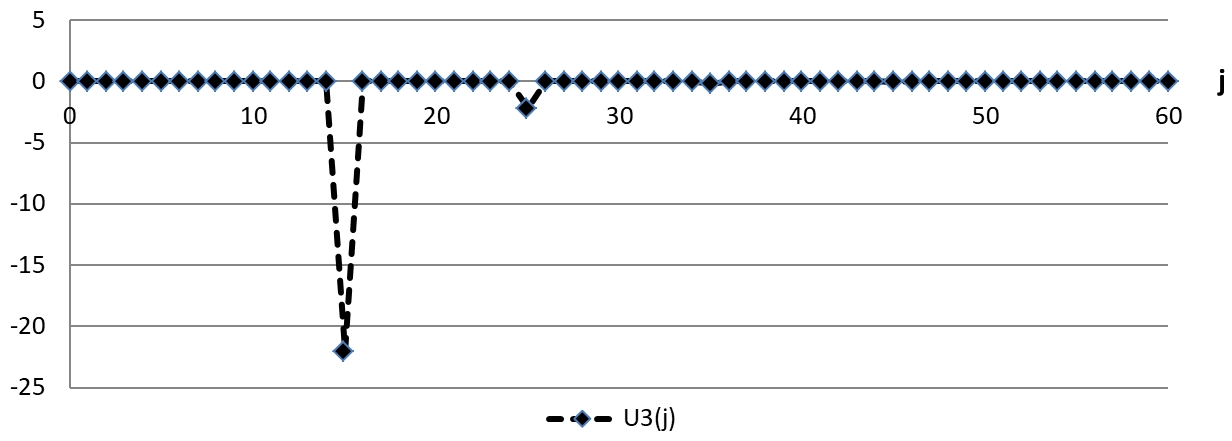
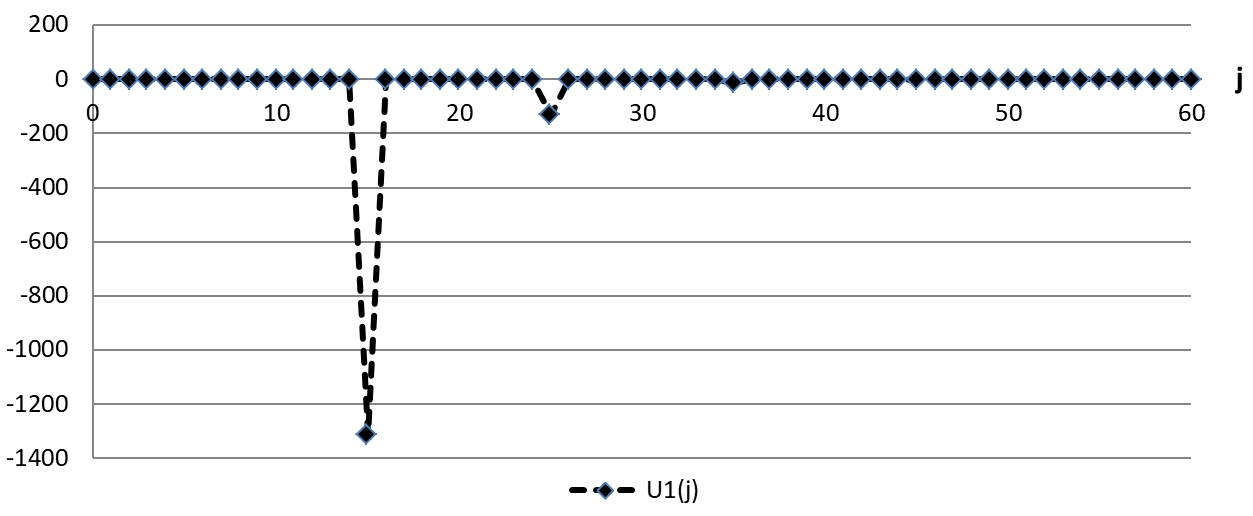
Отсюда следует вывод, что для предотвращения хаотичных макроэкономических явлений необходимо своевременно осуществлять превентивные корректирующие меры. Полученная в явном виде аналитическая формула (9) позволяет определять размеры и время проведения упреждающих корректировок. На рисунках 8 и 9 показана динамика корректирующих операций, направленных на стабилизацию макроэкономической цикличности.
Рис. 8 – Смоделированный график управления ![]() для стабилизации цикличности ВВП
для стабилизации цикличности ВВП
Рис. 9 – Смоделированный график управления ![]() для стабилизации цикличности инвестиций
для стабилизации цикличности инвестиций
Из рисунков 8 и 9 видно, что графики для функций управления имеют импульсообразную форму с быстро затухающей амплитудой. Это указывает на то, что оперативные меры по упреждению хаотичности имеют точечный характер и их необходимо активно проводить в начальный период формирования хаотичной динамики, после чего эти меры сокращаются до нуля. Таких точечных корректировок достаточно для нейтрализации макроэкономического хаоса и поддержания устойчивой цикличности. Положительные значения функций управления указывают на необходимость увеличения ВВП и инвестиций, а отрицательные значения сигнализируют о необходимости снижения ВВП и инвестиций.
Верификацию полученной модели (8)-(10) осуществим на основании статистических данных по ВВП и инвестициям Китая [4], [5]. Подберем нормировочные коэффициенты ![]() так, чтобы траектории
так, чтобы траектории ![]() колебались соответственно в пределах от
колебались соответственно в пределах от ![]() . В результате вычислений получается
. В результате вычислений получается
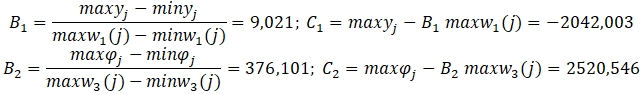
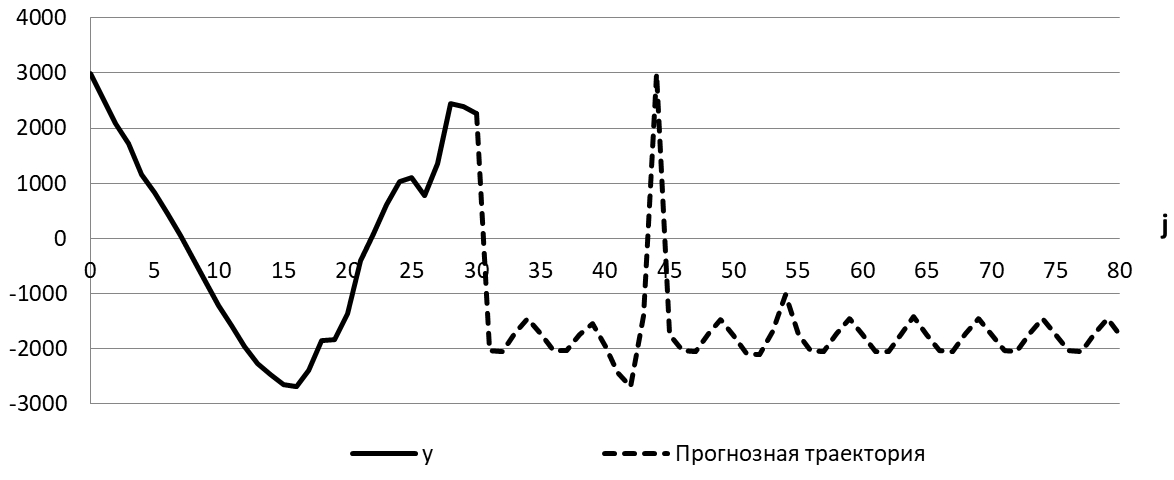
Рис. 10 – Квазипериодическая и смоделированная прогнозная траектории для ВВП
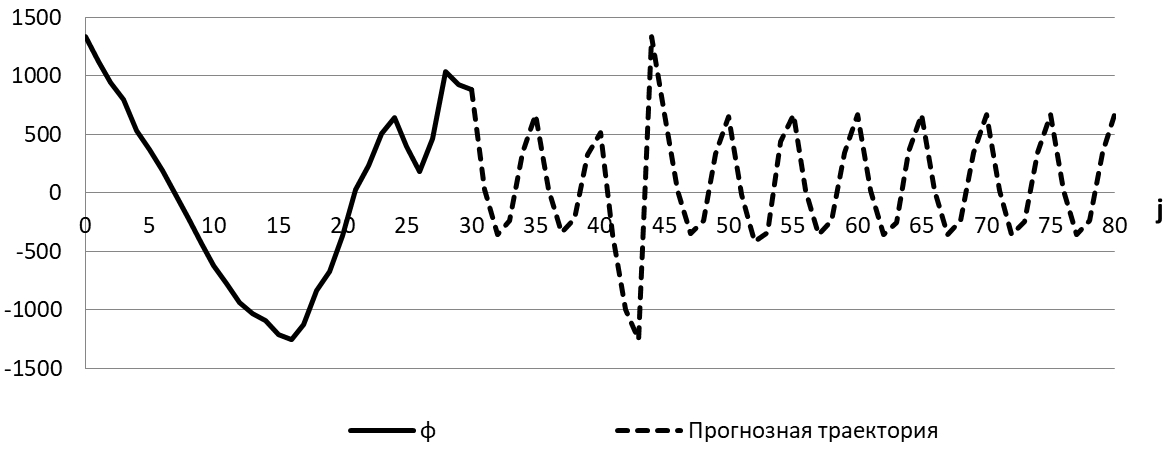
Рис. 11 – Квазипериодическая и смоделированная прогнозная траектории для инвестиций
Поскольку ![]() , то на основании (4) и (11) и с учетом «склейки» графиков в 2020 году (то есть в точке
, то на основании (4) и (11) и с учетом «склейки» графиков в 2020 году (то есть в точке ![]() ) получаем формулы для моделирования прогнозов по долгосрочному макроэкономическому росту
) получаем формулы для моделирования прогнозов по долгосрочному макроэкономическому росту
![]() (13)
(13)
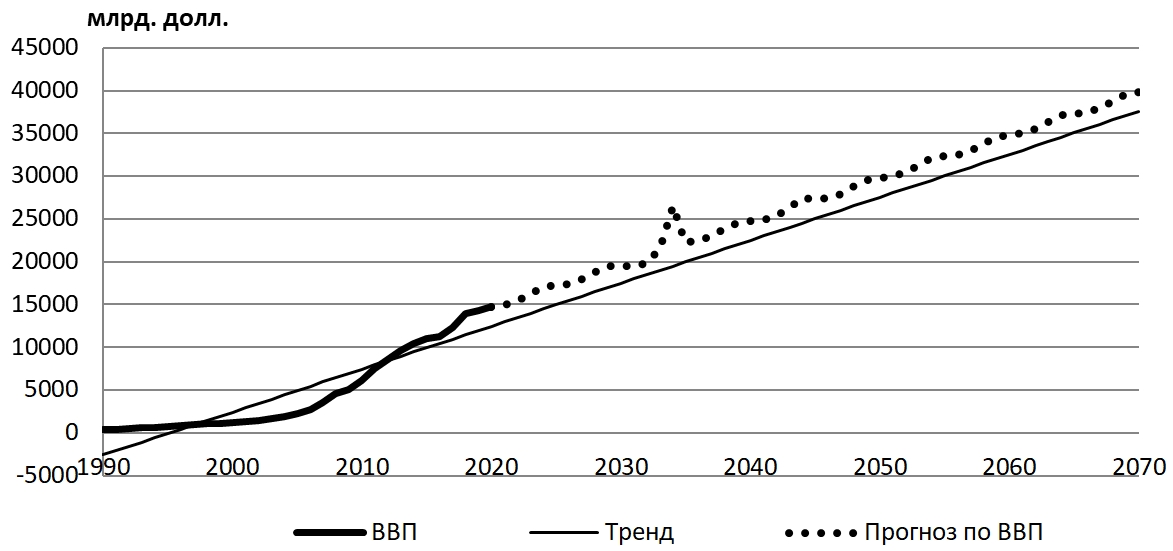
Рис. 12 – Долгосрочный прогноз по ВВП Китая
Рис. 13 – Долгосрочный прогноз по инвестициям Китая
Рисунки 12 и 13 содержат графики полученных по формулам (12)-(13) долгосрочных прогнозов для ВВП и инвестиций Китая. Коэффициент корреляции между смоделированными прогнозными значениями ![]() и реальными показателями ВВП
и реальными показателями ВВП ![]() равен 0,901 и является статистически значимым, так как по критерию Стьюдента Тнабл =11,184 > 2,756= Ткрит при уровне значимости α=0,005. Коэффициент корреляции между смоделированными прогнозными значениями
равен 0,901 и является статистически значимым, так как по критерию Стьюдента Тнабл =11,184 > 2,756= Ткрит при уровне значимости α=0,005. Коэффициент корреляции между смоделированными прогнозными значениями ![]() и реальными показателями инвестиций
и реальными показателями инвестиций ![]() равен 0,912 и является статистически значимым, так как по критерию Стьюдента Тнабл =11,973 > 2,756= Ткрит при уровне значимости α=0,005. Следовательно, математическая модель (8)–(9) вполне адекватно генерирует прогнозные траектории.
равен 0,912 и является статистически значимым, так как по критерию Стьюдента Тнабл =11,973 > 2,756= Ткрит при уровне значимости α=0,005. Следовательно, математическая модель (8)–(9) вполне адекватно генерирует прогнозные траектории.
Разработанная модель (8)–(9) является не только инструментом эффективного и адекватного прогнозирования. Основное достоинство этой модели заключается в том, что она дает возможность практического управления динамикой ВВП и инвестиций в целях стабилизации долгосрочного макроэкономического роста. Таким образом, появляется возможность в реальности обеспечивать спрогнозированное развитие экономики.
Заключение
На основании полученных результатов можно сделать вывод, что для предотвращения высокой волатильности и хаотичной динамики в макроэкономической цикличности необходимо своевременно осуществлять упреждающие корректирующие меры. Предложенная модель (8)-(9) может использоваться в условиях отсутствия существенных внешних шоков как вспомогательный инструмент для стабилизации циклических тенденций, возникающих в реальной экономике, и для формирования устойчивой периодической траектории экономического роста. Формула (9) позволяет точно вычислять размеры и время для необходимых упреждающих макроэкономических корректировок. Таким образом, разработан инструментарий по моделированию управленческих мер, которые могут способствовать стабилизации макроэкономической динамики.
Разработанные в данной статье методы довольно удобны с практической точки зрения и легко адаптируются к рыночным реалиям. Дискретная система (8) выполняет функцию имитационного моделирования и за счет варьирования начальных условий генерирует разнообразное хаотичное движение показателей ВВП и инвестиций. Модель (8) с управлением (9) позволяет проводить анализ возможностей, способствующих выводу макроэкономической динамики на устойчивую периодическую траекторию. Полученная модель дает возможность предварительно оценить параметры управленческих решений, направленных на предотвращение серьезных отклонений от оптимального тренда. Поскольку с помощью формулы (9) можно вычислить точные размеры и время для необходимых импульсообразных корректировок, то модель (8)-(9) может быть полезной при разработке и осуществлении мер, направленных на стабилизацию экономического развития.
Полученные в данной статье результаты являются новым дополнением к исследованиям [9], [10], [11], посвященным моделированию макроэкономических периодических трендов и стабилизации циклических процессов с помощью методов теории управления хаосом.
| Конфликт интересов Не указан. | Conflict of Interest None declared. |
Список литературы / References
- Акаев А.А. О новой методологии долгосрочного циклического прогнозирования динамики развития мировой системы и России / А.А. Акаев, В. А. Садовничий // Прогноз и моделирование кризисов и мировой динамики / Ред. А.А. Акаев, А.В. Коротаев, Г.Г. Малинецкий. – М.: ЛКИ/URSS. – 2010. – С. 5–69.
- Акаев А.А. Влияние деловых циклов на долговременный экономический рост / А.А. Акаев // Доклады Академии наук. – 2008. – 421/1– С. 29–33.
- Акаев А.А. Моделирование и прогнозирование глобального, регионального и национального развития / Отв. ред. А.А. Акаев, А.В. Коротаев, Г.Г. Малинецкий, С.Ю. Малков. – М.: ЛИБРОКОМ, 2011. – 488 с.
- Институт экономики и права Ивана Кушнира [Электронный ресурс] URL: https://be5.biz/makroekonomika/gdp/cn.html (дата обращения: 29.08.2021).
- Институт экономики и права Ивана Кушнира [Электронный ресурс] URL: https://be5.biz/makroekonomika/capital_formation/cn.html (дата обращения: 29.08.2021).
- Pyragas K. Continuous control of chaos by self-controlling feedback / K. Pyragas // Physics Letters A. – 1992. – vol. 170. – p. 421-428.
- Леонов Г.А. Стабилизация по Пирагасу дискретных систем запаздывающей обратной связью с периодическим импульсным коэффициентом усиления / Г.А. Леонов, К.А. Звягинцева // Вестник СПбГУ. Серия 1. Математика. Механика. Астрономия. – 2015. – т. 2(60). – вып. 3. – С. 342-353.
- Leonov G.A. Pyragas stabilization of discrete systems via delayed feedback with periodic control gain / G.A. Leonov, K.A. Zvyagintseva, O.A. Kuznetsova // IFAC-PapersOnLine. – 2016. – vol. 49-14. – p. 56-61.
- Петряков А.А. Моделирование коротких экономических волн и устранение рыночного хаоса / А.А. Петряков // Экономика и предпринимательство. – 2017. – № 2(ч.2). – С. 76-86.
- Звягинцев А.И. Моделирование вспомогательных мер по стабилизации ценовой динамики на рынке нефти / А.И. Звягинцев // Современная экономика: проблемы и решения. – 2019. – № 6(114). – С. 8-24.
- Звягинцев А.И. О контроле хаотичной динамики на валютном рынке / А.И. Звягинцев // Экономические отношения. – 2019. – Т.9 – № 3. – С. 2349-2366.
Список литературы на английском языке / References in English
- Akaev А.А. O novoy metodologii dolgosrochnogo tsiklicheskogo prognozirovaniya dinamiki razvitiya mirovoy sistemi i Rossii [On a new methodology for long-term cyclical forecasting of the development dynamics for both the world system and Russia] / А.А. Akaev, V.А. Sadovnichiy // Prognoz i modelirovanie krizisov i mirovoy dinamiki [Forecasting and modeling of crises and world dynamics] / ed. by А.А. Akaev, А.V. Korotaev, G.G. Malinetskiy. – М.: LKI/URSS. – 2010. – P. 5–69. [in Russian]
- Akaev А.А. Vliyanie delovih tsiklov na dolgovremenniy ekonomicheskiy rost [The impact of business cycles on long-term economic growth] / А.А. Akaev // Doklady Akademii nauk [Reports of the Academy of Sciences]. – 2008. – 421/1– P. 29–33. [in Russian]
- Akaev А.А. Modelirovanie i prognozirovanie global’nogo, regional’nogo i natsional’nogo razvitiya [Modeling and forecasting global, regional, and national development] / ed. by А.А. Akaev, А.V. Korotaev, G.G. Malinetskiy, S.J. Мalkov. – М.: LIBROKOM, 2011. – 488 p. [in Russian]
- Institut ekonomiki i prava Ivana Kushnira [Institute of Economics and Law Ivan Kushnir] [Electronic resource] URL: https://be5.biz/makroekonomika/gdp/cn.html (accessed: 29.08.2021). [in Russian]
- Institut ekonomiki i prava Ivana Kushnira [Institute of Economics and Law Ivan Kushnir] [Electronic resource] URL: https://be5.biz/makroekonomika/capital_formation/cn.html (accessed: 29.08.2021). [in Russian]
- Pyragas K. Continuous control of chaos by self-controlling feedback / K. Pyragas // Physics Letters A. – 1992. – vol. 170. – P. 421-428.
- Leonov G.А. Stabilizatsiya po Piragasu diskretnykh sistem zapazdyvayushej obratnoj svyaz’yu s periodicheskim impul’snym koeffitsientom usileniya [Stabilization by Pyragas of discrete systems with the delayed feedback with pulse periodic gain] / G.А. Leonov, К.А. Zvyagintseva // Vestnik SPbGU. Seriya 1. Matematika. Mekhanika. Astronomiya [St. Petersburg State University Bulletin. Series 1. Mathematics. Mechanics. Astronomy]. – 2015. – V. 2(60). – №. 3. – P. 342-353. [in Russian]
- Leonov G.A. Pyragas stabilization of discrete systems via delayed feedback with periodic control gain / G.A. Leonov, K.A. Zvyagintseva, O.A. Kuznetsova // IFAC-PapersOnLine. – 2016. – Vol. 49-14. – P. 56-61.
- Petryakov A.A. Modelirovanie korotkikh ekonomicheskikh voln i ustranenie rynochnogo khaosa [Modelling short economic waves and eliminating market chaos] / А.А. Petryakov // Ekonomika i predprinimatel’stvo [Journal of economy and entrepreneurship]. – 2017. – Vol. 11. – № 2-2. – P. 76-86. [in Russian]
- Zvyagintsev А.I. Modelirovanie vspomogatel’nikh mer po stabilizatsii tsenovoy dinamiki na rynke nefti [Modelling of the supplementary measures for the stabilization of oil market price dynamics] / А.I. Zvyagintsev // Sovremennaya ekonomika; problemi i resheniya [Modern Economics: problems and solutions]. – 2019. – № 6(114). – P. 8-24. [in Russian]
- Zvyagintsev А.I. O kontrole khaotichnoy dinamiki na valyutnom rinke [On controlling chaotic dynamics in the foreign exchange market] / А.I. Zvyagintsev // Ekonomicheskie otnosheniya [Journal of international economic affairs]. – 2019. – V.9 – № 3. – P. 2349-2366. [in Russian]