УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ ПРИ ИЗМЕРЕНИИ ВЫСОТНЫХ ОТМЕТОК С ПОМОЩЬЮ GNSS-СИСТЕМ И ИХ ПРИМЕНЕНИЕ ДЛЯ ГЕОДИНАМИЧЕСКОГО МОНИТОРИНГА НЕФТЕГАЗОНОСНЫХ РАЙОНОВ

УРАВНИТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ ПРИ ИЗМЕРЕНИИ ВЫСОТНЫХ ОТМЕТОК С ПОМОЩЬЮ GNSS-СИСТЕМ И ИХ ПРИМЕНЕНИЕ ДЛЯ ГЕОДИНАМИЧЕСКОГО МОНИТОРИНГА НЕФТЕГАЗОНОСНЫХ РАЙОНОВ

Научная статья

Цвяк А.В.^1, *, Нестеренко М.Ю.², Никифоров С.Э.³, Белов В.С.⁴

¹ ORCID: 0000-0002-4561-7034;

² ORCID: 0000-0003-1465-0752;

³ ORCID: 0000-0001-5167-0408;

⁴ ORCID: 0000-0002-1215-3595;

^{1, 2, 4} Оренбургский федеральный исследовательский центр УрО РАН, Оренбург, Россия;

³ Горный институт НИТУ «МИСиС», Москва, Россия

* Корреспондирующий автор (tsviak[at]rambler.ru)

Аннотация

В статье обоснована необходимость геодинамического мониторинга на больших по площади территориях нефтегазодобычи с высокой точностью. Один из наиболее эффективных способов геодинамического мониторинга основан на высокоточных GNSS-измерениях с использованием уравнительных вычислений. Выполнена адаптация математического аппарата уравнительных вычислений для решения задач геодинамического мониторинга с помощью GNSS-систем.

Выполнены реализация и апробирование предложенного математического обеспечения на созданном отделом геоэкологии ОФИЦ УрО РАН геодинамическом полигоне в районе Оренбургского нефтегазоконденсатного месторождения. Для организации системы мониторинга геодинамических процессов на объектовом уровне мониторинга состояния недр, в 2014-2017 гг. заложено 4 фундаментальных репера, составляющих каркас наблюдательной сети. За период с 2014 по 2019 годы были получены результаты наблюдений за деформацией земной поверхности на пунктах наблюдения геодинамического полигона в виде относительного изменения высотной отметки. За начальное значение принята высотная отметка, полученная при первом измерении координаты на соответствующем пункте наблюдения в 2014 г. Далее рассчитаны разницы между текущим значением высотной отметки и значением высотной отметки, полученным при первом измерении.

Ключевые слова: геодинамика, сейсмическая активность, контроль проявлений геодинамических процессов, GNSS-измерения, уравнительные вычисления.

EQUALIZATION CALCULATIONS IN TOPOGRAPHIC ELEVATION MEASUREMENT USING GNSS-SYSTEMS AND THEIR APPLICATION FOR GEODYNAMIC MONITORING OF OIL AND GAS AREAS

Research article

Tsvyak A.V. ^1, *, Nesterenko M.Yu.², Nikiforov S.E.³, Belov V.S.⁴

¹ ORCID: 0000-0002-4561-7034;

² ORCID: 0000-0003-1465-0752;

³ ORCID: 0000-0001-5167-0408;

⁴ ORCID: 0000-0002-1215-3595;

^{1, 2, 4} Orenburg Federal Research Center, Ural Branch of the Russian Academy of Sciences, Orenburg, Russia;

³ The College of Mining of NUST MISIS, Moscow, Russia

* Corresponding author (tsviak[at]rambler.ru)

Abstract

The paper substantiates the need for highly accurate geodynamic monitoring on large areas of oil and gas production. One of the most effective geodynamic monitoring methods is based on high-precision GNSS measurements using equalization calculations. The authors adapted the mathematical basis of equalization calculations for solving the problems of geodynamic monitoring using GNSS systems.

Implementation and testing of the proposed software were carried out on the geodynamic testing ground created by the Department of Geoecology of the Ural Branch of the Russian Academy of Sciences in the region of the Orenburg oil and gas condensate field, to organize a monitoring system for geodynamic processes at the facility level for monitoring the state of the subsoil, in 2014-2017. Four fundamental benchmarks were laid to make up the basis of the observational network. The results of observations of the deformation of the earth's surface at observation points of the geodynamic test site were obtained in the form of a relative change in elevation for the period from 2014 to 2019. The initial value is the elevation obtained during the first measurement of the coordinate at the corresponding observation point in 2014. Further, the differences between the current value of the elevation and the value of the elevation obtained during the first measurement were calculated.

Keywords: geodynamics, seismic activity, control of manifestations of geodynamic processes, GNSS measurements, equalizing calculations.

Введение

Геодинамика платформенных территорий плохо изучена, т.к. платформенные территории принято считать геодинамически малоактивным и слабосейсмичным. К таким территориям относится Южное Предуралье, на примере которого выполнены данные исследования. Южное Предуралье включает юго-восточную часть Восточно-европейской платформы, южную часть Предуральского прогиба и северный борт Прикаспийской синеклизы. И тем более остаются слабоизученными геодинамические процессы в разрабатываемых месторождениях нефти и газа платформенных территорий. В связи с этим назрела необходимость разработки научно-методологических основ исследования закономерностей формирования и развития геодинамических процессов в естественных и техногенно измененных условиях, оценки и мониторинга геодинамического и геоэкологического состояния недр нефтегазоносных территорий (на примере Южного Предуралья) [1], [3], [4].

В условиях развития природных геодинамических и гидрогеодинамических процессов, блоково-разломного строения земной коры интенсивная добыча нефти и газа в крупных нефтегазоносных районах нарушает природную, включая геологическую, среду, происходят существенные изменения в гео-, гидрогео- и гидрогазодинамических процессах в верхней части земной коре на площади достигающей пяти-семи тысяч квадратных километров и более. В западной части Оренбургской области разрабатывается более 120 месторождений нефти и газа, так что области техногенных изменений, возникающие при их разработке, пересекаются. Это провоцирует появление многих экологических проблем, оказывающих негативное влияние на развитие природы и жизнедеятельность населения в регионе. Например, остро стоит проблема снижения негативных последствий разработки месторождений нефти в Национальном парке «Бузулукский бор». Выявление и исследование закономерностей формирования и развития гео- и гидрогеодинамических процессов в естественных и техногенно измененных условиях, оценки и мониторинга геодинамического и геоэкологического состояния недр позволят применять экологически безопасные технологии разработки месторождений нефти и газа [4], [6], [7].

Таким образом, необходимо выполнение геодинамического мониторинга на больших по площади территориях нефтегазодобычи достигающих 50 тыс. км² с высокой точностью. Один из наиболее эффективных способов геодинамического мониторинга основан на высокоточных GNSS-измерениях с использованием уравнительных вычислений [3].

Уравнительные вычисления выполняются при математической обработке результатов измерений в маркшейдерско-геодезических построениях. Существует множество методов и программных средств для выполнения уравнительных вычислений при реализации наземной геодезии – засечках, ходах, сетях и проч. Однако применение подобных методов и средств при высокоточных GNSS-измерениях требует их адаптации и существенной доработки. Например, нормативными документами требуется при выполнении GNSS-измерений включение в сеть не менее пяти пунктов сетей более высокой точности, которые следует считать безошибочными, как правило, это пункты государственной геодезической сети (ГГС) или референцные станции. На практике использование существующих средств, реализующих уравнительные вычисления, в большинстве случаев не дает решения по причине неточности координат пунктов ГГС и разреженности сети референцных станций.

Уравнительные вычисления при измерении высотных отметок с помощью GNSS-систем

Обозначим истинные значения измеренных с помощью GNSS-систем величин через X₁, … ,X_N, где N – число измеренных величин, а результаты измерений обозначим через x₁, … , x_N. А координаты L пунктов ГГС обозначим через M₁, … ,M_L .

Математические отношения между истинными значениями измеренных величин и исходными данными задаются условными уравнениями:

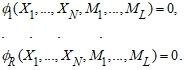       (1)

При подстановке в уравнения (1) измеренных значений и координат пунктов ГГС, вследствие ошибок измерений и координат пунктов ГГС в правой части окажутся невязки w и получатся уравнения невязок:

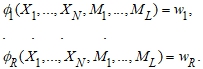      (2)

В (Гордеев, 2004) [8] обосновывается использование метода наименьших квадратов для выполнения уравнительных процедур для его применения в наземных геодезических измерениях.

В случае использования GNSS-измерений получаем N значений координат неизвестной точки X. Для уравнивания вводим поправки v₁, … ,v_N, равные v_i=X-X_i, где i=1..N. Минимизируя функцию, получим оценку  искомых координат точки X. В рассмотренном случае координаты M₁, … ,M_L считаются абсолютно точными.

Для выполнения уравнительных процедур при измерении высотных отметок с помощью GNSS-систем возможно использование коррелатного способа уравнивания. Согласно (Гордеев, 2004) [8] в нивелирных ходах встречаются только два вида условий:

• замкнутого хода (см. рисунок 1) – сумма превышений в замкнутом нивелирном ходе должна равняться нулю: 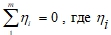, где - истинные значения высотных отметок при относительных измерениях в системе «база-ровер», m – число измерений;
• разомкнутого хода – сумма превышений в разомкнутом нивелирном ходе должна равняться разности высотных отметок исходных реперов: 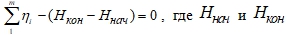 - высотные отметки исходных реперов в начале и конце нивелирного хода.

Исследование точности измерений высотных отметок с помощью GNSS-систем позволяет говорить об их неравноточности. Точность измерений зависит от условий приема сигналов спутников, расстояний до базовой или референцной станции, продолжительности съемки и др. и может быть измерена с помощью среднеквадратичного отклонения (СКО) измерений. Поэтому целесообразно использование весовых коэффициентовp₁, … ,p_N, обратно пропорциональных СКО при уравнивании – чем больше СКО, тем больше поправка может быть внесена при использовании метода наименьших квадратов (МНК). Весовые коэффициент могут быть вычислены по формуле 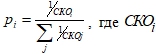, где  - среднеквадратическое отклонение при i-ом измерении. Таким образом, для уравнивания вводим поправки v₁, … ,v_N, равные v_i=X-X_i, где i=1..N. Минимизируя функцию, получим оценку  искомых координат точки X.

Результаты уравнительных вычислений при измерениях на геодинамическом полигоне в районе Оренбургского нефтегазоконденсатного месторождения

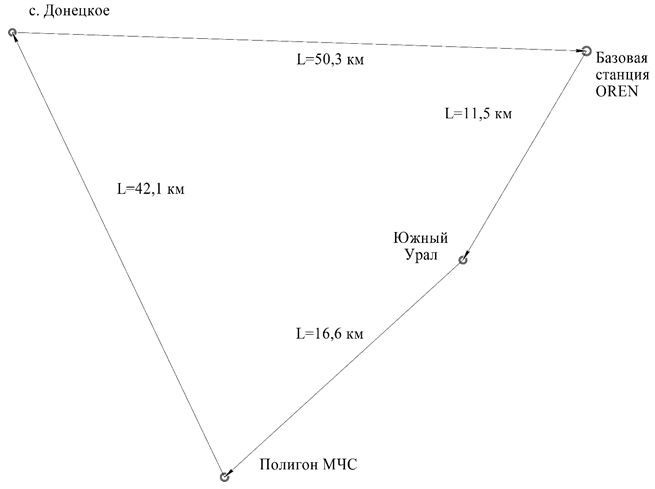
Реализация и апробирование предложенного математического обеспечения выполнено на созданном отделом геоэкологии ОФИЦ УрО РАН геодинамическом полигоне в районе Оренбургского нефтегазоконденсатного месторождения. Для организации системы мониторинга геодинамических процессов на объектовом уровне мониторинга состояния недр, в 2014-2017 гг. заложено 4 фундаментальных репера, составляющих каркас наблюдательной сети (рис. 1). В качестве исходного пункта 1 была использована базовая станции OREN сети референцных станций «Смартнет» ООО «Навгеоком». Второй пункт расположен в центре гидродинамической воронки подземных вод на территории месторождения (полигон МЧС). Третий пункт - контрольный, расположен в п. Южный Урал (находится за пределами месторождения, но в пределах гидродинамической воронки). Четвертый пункт расположен на Донецко-Сыртовском выступе, находится за пределами техногенного воздействия добычи углеводородного сырья и направлен на контроль развития природных геодинамических процессов [6].

На пунктах используются двухчастотные GNSS-приемники LeicaViva. Заявленные производителем характеристики позволяют достичь приемлемой точности контроля.

Для оценки точности измерений проведены наблюдения по замкнутому ходу, включающему базовую станцию OREN и пункты 2-4.

Наблюдения на пунктах велись в следующем порядке. Для первого наблюдения ровер устанавливали на втором пункте наблюдения. Для постобработки использовали данные, полученные c приемника, расположенного на опорном пункте базовой станции OREN. Далее устанавливали базовый приемник на второй пункт и использовали его для постобработки данных, полученных с ровера, установленного на третьем пункте. Здесь значения координат пункта 2 принимались по данным, полученным в предыдущем наблюдении. И так далее, по схеме, в соответствие с рисунком 1. В последнем наблюдении получили координаты опорного пункта.

 

Рис. 1 – Порядок замеров на точках наблюдения

 

Результаты измерений представлены в таблице 1.

Из таблицы 1 следует, что невязка по высоте на опорном пункте составила 6,4 мм. Значение допустимой невязки принято 10 мм [9] (Инструкция по нивелированию I, II, III и IV классов ГКИНП (ГНТА)-03-010-03, МОСКВА, ЦНИИГАИК. 2004).

Для выполнения уравнительных процедур при измерении высотных отметок с помощью GNSS-систем возможно использование коррелатного способа уравнивания при условии замкнутого хода.

За период с 2014 по 2019 годы нами получены результаты наблюдений за деформацией земной поверхности на пунктах наблюдения геодинамического полигона в виде относительного изменения высотной отметки (Δ). За начальное значение принята высотная отметка, полученная при первом измерении координаты на соответствующем пункте наблюдения в 2014 г. Далее рассчитаны разницы между текущим значением высотной отметки и значением высотной отметки, полученным при первом измерении.

 

Таблица 1 – Результаты измерений координат пунктов наблюдения

Пункты наблюдения	Координаты			Уравненная высотная отметка, м	СКО, м	Весовой коэф.
Опорный (OREN)	51°45'18.33434" С	55°05'50.99196"В	99,2204 м	99,2204	0,005577	0,109313
Второй	51°44'08.99253" С	55°01'55.50476" В	76,3954 м	76,3927	0,004306	0,141586
Третий	51°37'04.53764" С	54°45'09.25647" В	101,6629 м	101,6581	0,001628	0,374551
Четвертый	51°54'03.15069" С	54°24'34.61231" В	186,8683 м	186,8627	0,001628	0,374551
Опорный	51°45'18.33224" С	55°05'50.99472" В	99,2268 м	99,2204	0,005577	0,109313
Невязка по высоте на опорном пункте			0,0064 м	0

 

В целом, можно отметить, что геодинамическая обстановка на пунктах наблюдения является спокойной. Величины вертикальных деформаций земной поверхности не велики.

Заключение

В результате выполненных исследований обоснована необходимость геодинамического мониторинга на больших по площади территориях нефтегазодобычи достигающих 50 тыс. км² и более с высокой точностью. Один из наиболее эффективных способов геодинамического мониторинга основан на высокоточных GNSS-измерениях с использованием уравнительных вычислений.

Предложенное математическое обеспечение реализовано и апробировано на созданном отделом геоэкологии ОФИЦ УрО РАН геодинамическом полигоне в районе Оренбургского нефтегазоконденсатного месторождения и получены результаты с достаточной точностью.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Adushkin V.V. Seismicity in the oil field / V.V. Adushkin, V.N. Rodionov, S. Turuntaev, A.E. Yudin // Oilfield Rev. – – V. 12(2). – P. 2–17.
2. Gibowicz S.J. Seismicity induced by mining: Ten years later / S.J. Gibowicz, S. Lasocki // Adv. Geophys. – – №44. – P. 39–180.
3. Tsviak A.V Modern Technogenic Geodynamics of Platform Territories by Example of Southern Cis-Urals. / A.V. Tsviak, M.Yu. Nesterenko, A.M. Nesterenko // Proceedings of the International Symposium “Engineering and Earth Sciences: Applied and Fundamental Research” (ISEES 2018). doi:10.2991/isees-18.2018.100
4. Baker M.R. Geologic and oil field controls on earthquakes in the War-Wink Field, Delaware Basin / M.R. Baker, D.I. Doser, M. Luo // Bulletin – West Texas Geol. – – №1. – P. 5–12.
5. Suckale J. Induced seismicity in hydrocarbon fields / J. Suckale // Adv Geophys. – – №51. – P. 55–106.
6. Нестеренко М.Ю. Природно-техногенная геодинамика и сейсмическая активность и их влияние на объекты повышенной опасности в Оренбургской области / М.Ю. Нестеренко, М.С. Карпюк, А.В. Цвяк, О.А. Капустина // Проблемы анализа риска. – – № 3. – С. 32-39.
7. Нестеренко М.Ю. Геоэкологические проблемы на нефтегазовых месторождениях Бузулукского бора. / М.Ю. Нестеренко, Ю.М. Нестеренко // Бюллетень Оренбургского научного центра УрО РАН. – – № 2. – С. 9.
8. Гордеев В.А. Теория ошибок измерений и уравнительные вычисления: учебное пособие для вузов/ В.А. Гордеев. - Екатеринбург: Изд-во УГГУ– – 429 с.
9. Инструкция по нивелированию I, II, III и IV классов ГКИНП (ГНТА)-03-010-03, МОСКВА, ЦНИИГАИК. 2004.

Список литературы на английском языке / References in English

1. Adushkin V.V. Seismicity in the oil field / V.V. Adushkin, V.N. Rodionov, S. Turuntaev, A.E. Yudin // Oilfield Rev., vol. 12(2), PP. 2–17, 2000.
2. Gibowicz S.J. Seismicity induced by mining: Ten years later / J. Gibowicz, S. Lasocki // Adv. Geophys. – 2001 – № 44. – PP. 39–180.
3. Tsviak A.V, Nesterenko M.Yu., Nesterenko A.M. Proceedings of the International Symposium “Engineering and Earth Sciences: Applied and Fundamental Research” (ISEES 2018). Modern Technogenic Geodynamics of Platform Territories by Example of Southern Cis-Urals. doi:10.2991/isees-18.2018.100
4. Baker M.R. Geologic and oil field controls on earthquakes in the War-Wink Field, Delaware Basin / M.R. Baker, D.I. Doser, M. Luo // Bulletin – West Texas Geol. №1, PP 5–12, 1991.
5. Suckale J. Induced seismicity in hydrocarbon fields / J. Suckale // Adv Geophys. – 2009. – № 51. – PP. 55–106.
6. Nesterenko Ju.M. Sejsmichnost' v rajonah dobychi uglevodorodov Juzhnogo Predural'ja [Natural and technogenic geodynamics and seismic activity and their influence on high-risk objects in the Orenburg region] / Ju.M. Nesterenko, Nesterenko M.Ju., M.S. Karpjuk // Problemy analiza riska [Problems of risk analysis]. – 2010. – V. 7. – № 2. – P. 48-54. [in Russian]
7. Nesterenko M.Ju. Gidrogeologicheskie processy i ih modelirovanie v rajonah dobychi uglevodorodov na primere Juzhnogo Predural'ja [Geoecological problems of oil and gas deposits in buzulukskiy Bor]. / M.Ju. Nesterenko, Ju.M. Nesterenko // Vest. OGU [Bulletin of the Orenburg scientific center]. – 2010. – № 9. – P. 122-127. [in Russian]
8. Gordeev V.A. Teorija oshibok izmerenij i uravnitel'nye vychislenija: uchebnoe [Theory of measurement errors and equation calculations]: textbook for universities / V.A. Gordeev. – Ekaterinburg: Publishing house of – 2004. – 429 p. [in Russian]
9. Instrukcija po nivelirovaniju I, II, III i IV klassov GKINP (GNTA)-03-010-03 [Instructions for leveling I, II, III and IV classes of SKINP (GNTA)-03-010-03]. – MOSKVA. – CNIIGAIK. – 2004. [in Russian]