О НАЗНАЧЕНИИ ПАРАМЕТРОВ УНИВЕРСАЛЬНОЙ МОДЕЛИ ДЕФОРМИРОВАНИЯ И РАЗРУШЕНИЯ БЕТОНА

О НАЗНАЧЕНИИ ПАРАМЕТРОВ УНИВЕРСАЛЬНОЙ МОДЕЛИ ДЕФОРМИРОВАНИЯ И РАЗРУШЕНИЯ БЕТОНА

Научная статья

Котов А.А.^1, *, Власенко В.Н.²

¹ ORCID: 0000-0003-4052-6376;

^{1, 2} Мурманский государственный технический университет, Мурманск, Россия

* Корреспондирующий автор (akot53[at]yandex.ru)

Аннотация

Изложены основные положения универсальной модели деформирования и разрушения бетона (УМДРБ), способной описывать его поведение в составе железобетонных конструкций при любых режимах и длительностях прикладываемых воздействий. Модель опирается на стандартные характеристики бетона, определяемые действующими нормативными документами, а также содержит новые, нетрадиционные параметры, которые предлагается определять по результатам испытания бетона при его одноосном нагружении с разными скоростями роста нагрузки. Предложены конкретные практические рекомендации по способам назначения всех этих характеристик, необходимых для эффективного применения УМДРБ в практических расчетах железобетонных конструкций.

Ключевые слова: модель деформирования бетона, линейная и нелинейная ползучесть, теория разрушения.

ON APPOINTMENT OF PARAMETERS OF UNIVERSAL MODEL OF CONCRETE DEFORMATION AND DESTRUCTION

Научная статья

Kotov A.A.^1, *, Vlasenko V.N.²

¹ ORCID: 0000-0003-4052-6376;

^{1, 2} Murmansk State Technical University, Murmansk, Russia

* Corresponding author (akot53[at]yandex.ru)

Abstract

The article presents the main provisions of the universal model of deformation and destruction of concrete describing its behavior in the composition of reinforced concrete structures under any modes and durations of applied impacts. The model is based on standard characteristics of concrete, determined by the current regulatory documents, and contains new, unconventional parameters proposed to be determined based on the results of testing concrete under its uniaxial loading at different rates of load growth. Specific practical recommendations on the methods of appointing all these characteristics necessary for the effective use of concrete in practical calculations of reinforced concrete structures are proposed.

Keywords: concrete deformation model, linear and non-linear creeping, fracture theory.

Введение

Основные положения универсальной модели деформирования и разрушения бетона (УМДРБ) представлены в работах [1], [3], [4]. Для общего случая объемного напряженно-деформированного состояния они состоят в следующем.

Рассматривается бетон со стабильными во времени свойствами: его основные нормируемые характеристики – начальный модуль упругости E, начальный коэффициент поперечной упругой деформации v, мгновенные призменные сопротивления сжатию R_с и растяжению R_р – считаются не зависящими от времени.

Полная деформация  складывается из упругой деформации , деформации линейной обратимой ползучести  и деформации необратимой нелинейной ползучести :

    (1) Для упругой деформации справедлив закон Гука:    (2) здесь  - среднее напряжение (компонента шарового тензора напряжений),  – символ Кронекера:    (3)

Полностью обратимая и поэтому линейная деформация ползучести представлена традиционной формулой:

   (4)

Здесь индекс  в выражении  означает, что величина C  зависит от аргумента .

Деформация нелинейной ползучести в представляемой теории выражается через скорости изменения интенсивности  и компоненты шарового тензора  этих деформаций:

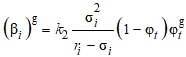    (5)

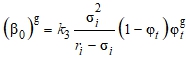    (6)

Здесь запись  означает, что t является аргументом функции φ. Точка в верхнем индексе означает дифференцирование по времени.

После интегрирования дифференциальных уравнений (5) и (6) интенсивность деформаций нелинейной ползучести и ее шаровой тензор раскладываются по компонентам этой деформации в соответствии с известным соотношением Мизеса:

      (7)

В формулах (5), (6) коэффициенты   – константы теории, подлежащие определению по результатам экспериментов;  – интенсивность напряжений:

      (8)

в (8)  – девиатор тензора напряжений.

Функция , обеспечивающая развертку необратимой деформации ползучести во времени, выражается через меру линейной ползучести:

   (9)

Переменная во времени величина   представляет собой текущий запас прочности в точке, такой, что разрушение материала в точке происходит тогда, когда интенсивность напряжений в этой точке достигает этой величины:

     (10)

В представляемой универсальной модели деформирования и разрушения бетона текущий запас прочности r_i определяется энергетическим соотношением

      (11)

Здесь G – начальный модуль сдвига бетона;   – константа теории, подлежащая определению по результатам экспериментов. Величина  представляет собой начальное эквивалентное сопротивление бетона разрушению в точке, которое может быть принято по какой-либо известной теории прочности; например, по классической теории Мора:

     (12)

или по теории П. П. Баландина:

     (13)

Здесь величина  хоть и называется начальным эквивалентным сопротивлением бетона, тем не менее не остается постоянной, а зависит от текущего напряженного состояния в точке, т. е. от времени. Величина  характеризует реальное сопротивление бетона, которое уменьшается по сравнению с  за счет деструктивных процессов в бетоне, характеризуемых величиной .

Величина  – это, согласно теории, полностью необратимая работа деформаций нелинейной ползучести, которая именно вследствие такой ее трактовки находится по формуле

      (14)

Здесь  - интенсивность скоростей деформаций необратимой ползучести. Компоненты  находятся дифференцированием компонент  из (7), а свертка  в интенсивность производится в соответствии с классическим определением интенсивности деформаций т. е. следующим образом:

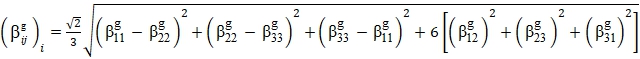      (15)

В соответствии с представленными выше соотношениями, новыми, нетрадиционными характеристиками материала, используемыми в теории, являются следующие величины:

- k₁ - параметр, характеризующий скорость диссипации энергии в процессе нелинейной ползучести;

- k₂ - параметр, характеризующий скорость роста интенсивности деформаций нелинейной ползучести в зависимости от интенсивности напряжений;

- k₃ - параметр, характеризующий скорость роста шарового тензора деформаций нелинейной ползучести в зависимости от интенсивности напряжений.

Кроме того, в процессе адаптации общих соотношений теории к описанию сравнительно простых частных случаев напряженно-деформированного состояния возникают еще некоторые не совсем традиционные, не описываемые в нормативных документах характеристики бетона, которые, тем не менее, являются обязательными для предварительного определения. К ним относится, прежде всего, значение меры линейной ползучести на асимптотически бесконечном времени: . Универсальная аппроксимация меры ползучести как функции времени может быть принята в виде суммы экспонент:

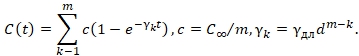       (16)

Тогда в этой форме представления вместе с  должны быть определены: количество экспонент m в их сумме, аппроксимирующей меру линейной ползучести; показатель  наиболее «медленной» экспоненты в их сумме, аппроксимирующей меру линейной ползучести; кратность d шага изменения показателя экспонент в мере линейной ползучести.

Во-вторых, должна быть априори определена величина  – коэффициент Пуассона для деформации нелинейной ползучести.

Основное содержание

Указать способы определения параметров УМДРБ, не являющихся общепринятыми, нужно так, чтобы для расчетов было бы достаточно действующих нормативных документов, и не требовалось бы новых трудоемких испытаний материала. Это можно сделать следующим образом.

Параметр k1, характеризующий влияние диссипации энергии в процессе нелинейной ползучести на уменьшение текущей прочности бетона, в соответствии с исследованиями [4], [5], посвященным апробации универсальной теории на экспериментальных кривых ползучести и диаграммах одноосного загружения бетона, можно принять

Параметр k₂, характеризующий скорость роста интенсивности деформаций нелинейной ползучести в зависимости от интенсивности напряжений, определяется из соотношения

где при условии, что уровни нагружения бетона не превышают его длительной прочности, параметр k₁₂ на основании результатов работы [4] определяется соотношением

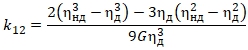       (17)

Здесь

    (18)    (19)

Уровень длительной прочности  является величиной, достаточно стабильной для бетонов разных классов, поэтому его более логично определять не из соотношения (19), а назначать независимо. Согласно экспериментальным исследованиям [6] можно принять ; однако вопрос о величине длительного сопротивления бетона сжатию должен быть еще изучен дополнительно. Согласно приведенным здесь соотношениям, например, для бетона В25 получается  .

Параметр , характеризующий скорость роста шарового тензора деформаций нелинейной ползучести в зависимости от интенсивности напряжений, определяется из соотношения  .

По результатам исследованиям (5), отношение скорости роста шарового тензора деформаций нелинейной ползучести и скорости роста интенсивности деформаций нелинейной ползучести можно принять . Для бетона В25 в этом случае получается  

Значение меры ползучести в бесконечности по времени, , можно связать с коэффициентом ползучести , значение которого постулируется нормативом СП 63.13330.2018 в зависимости от класса бетона и влажности среды. Из формулы (6.3) этого норматива

      (20) получается:  

Здесь величина  отражает деформационные свойства бетона на условно бесконечном отрезке времени. Поэтому в случае одноосного сжатия можно принять

      (21) Если напряжение  достаточно мало, т. е. если рассматривается невысокий уровень нагружения, при котором нелинейная ползучесть практически не проявляется, можно принять Полагая дальше   Получаем      (22) После подстановки (22) в (20) получается   откуда       (23) Для бетона В25 при средней влажности 40% – 75% ,  откуда следует .

Далее нужно решить вопрос об оптимальном количестве экспонент в форме (16). Чтобы сделать это аргументированно, приведем те параметры экспонент, с помощью которых ранее нами были аппроксимированы различные экспериментальные результаты [5]. Эти параметры показаны в табл. 1.

Таблица 1 – Параметры экспонент для аппроксимации меры линейной ползучести

 

Обобщая представленные в табл. 1 величины, можно для перекрытия всех возможных диапазонов принять для  наибольшее из приведенных значений, а для  – наименьшее. Принимаем округленно . Тогда параметр d можно получить из (16) следующим образом:

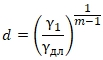     (24)

Вполне логично предположить, что определяющими в аппроксимации кривых ползучести и диаграмм сжатия являются самая медленная и самая быстрая экспоненты, а количество промежуточных экспонент не очень существенно. Продолжая эту логику, можно поставить вопрос об их минимально необходимом количестве, поскольку с большим количеством экспонент работать неудобно. Для решения этого вопроса нужно зафиксировать числовые параметры крайних экспонент и вычислить значения величины d при разных количествах экспонент m. Сохраняя унифицированные , из (24) получаем:

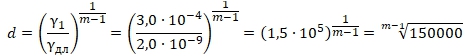       (25) Числовые значения d при разных значениях m представлены в табл. 2.  

Таблица 2 – Зависимость параметра d в форме (16) от количества экспонент m

m	2	3	4	5	6	7	8
d	150000	387	53,1	19,7	10,8	7,3	5,4

 

При шести экспонентах значение d получается достаточно круглым, причем это значение весьма близко к числу 10, т. е. к основанию порядка в десятичной системе счисления. Тогда можно принять, что при количестве экспонент 6 показатель каждой следующей экспоненты будет изменяться на порядок по сравнению с показателем предыдущей, т. е. в 10 раз. Таким образом, когда параметры экспонент не регламентируются никакими экспериментальными данными, можно принять:

     (26) При этом спектр показателей экспонент будет таким:     (27)

Однако этот формальный вывод не отвечает на вопрос о том, как количество экспонент влияет на форму кривых ползучести. Для получения аргументированного ответа построим кривые ползучести с разными количествами экспонент и с фиксированными крайними экспонентами. Именно, пусть , а параметр d определяется формулой (25) в зависимости от принятых показателей крайних экспонент и их количества m:

Связь между m и d отражена в табл. 3.  

Таблица 3 – Зависимость параметра d от количества экспонент m при унифицированных значениях γ₁ и γ_дл

m	2	3	4	5	6	7	8	9
d	100000	316	46,4	17,8	10,0	6,8	5,2	4,2

 

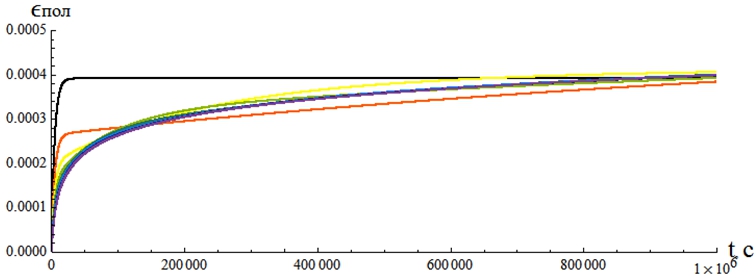
Для построения графика зависимости от времени деформации ползучести при разных количествах m экспонент в форме (16) составлена программа в среде Wolfram Mathematica. Далее на рис. 1 показаны результаты расчета по этой программе: кривые ползучести с разными значениями количества экспонент m, представленными в табл. 3.

Рис. 1 – Совмещенные кривые ползучести при m от 2 до 9

 

Здесь из общего ряда заметно выделяются черная, красная и желтая кривые ползучести, соответствующие значениям m = 2, 3 и 4. Остальные кривые ползучести не имеют существенных отличий друг от друга. Из этого можно сделать вывод, что минимально необходимое количество экспонент – пять. Однако в целях унификации расчетных формул и округления параметра кратности экспонент d рекомендуем для аппроксимации меры линейной ползучести использовать все-таки 6 экспонент, параметры которых представлены в (26) и (27).

Коэффициент Пуассона для деформации нелинейной ползучести  согласно работам [4] и [5] может быть получен из соотношения

    (28)

здесь верхние знаки относятся к сжатию, нижние – к растяжению. В соответствии с этим для бетона В25 при сжатии получается, при растяжении - . Из этих значений следует, что объемная деформация нелинейной ползучести отрицательна в обоих случаях, т. е. происходит уменьшение объема не только при сжатии (что естественно), но и при растяжении. Последнее можно объяснить тем, что в деструктивном процессе нелинейной ползучести структурные связи в поперечном направлении перестраиваются быстрее, чем в продольном. 

Заключение

Таким образом, можно констатировать, что в настоящей работе представлена полная и исчерпывающая информация о способах назначения реальных практических параметров универсальной модели деформирования и разрушения бетона. Используя эти указания, можно успешно применять представленную в начале статьи универсальную модель деформирования и разрушения бетона для описания поведения бетона в любых режимах его нагружения в составе железобетонных конструкций. 

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Харлаб В. Д. Энергетическая теория нелинейной ползучести и длительной прочности хрупко разрушающихся материалов (I). / В. Д. Харлаб // Механика стержневых систем и сплошных сред : межвуз. тематич. сб. тр. – Л.: ЛИСИ. – 1981. - Вып. 14. - С. 11–17.
2. Харлаб В. Д. Энергетическая теория нелинейной ползучести и длительной прочности хрупко разрушающихся материалов (II) / В. Д. Харлаб // Исследования по механике строительных конструкций и материалов : межвуз. тематич. сб. тр. – Л.: ЛИСИ. – 1982. - С. 136–141.
3. Харлаб В. Д. Энергетическая теория нелинейной ползучести и длительной прочности хрупко разрушающихся материалов (III) / В. Д. Харлаб // Исследования по теоретическим основам расчета строительных конструкций : межвуз. тематич. сб. тр. – Л.: ЛИСИ. – 1983. - С. 127–132.
4. Котов А. А. К теории ползучести и длительной прочности бетона / А. А. Котов. // Вестник МГТУ – 2002. - Том 5. - № 2. - С. 161–166.
5. Котов А. А. Теория деформирования и разрушения хрупких материалов: проверка по результатам простейших экспериментов / А. А. Котов. // Наука и образование – 2003 : материалы всероссийской научно-технической конференции, Мурманск / Мурманский гос. техн. ун-т. – Мурманск, 2003.
6. Яшин А. В. Деформации бетона под длительным воздействием высоких напряжений и его длительное сопротивление при сжатии / А. В. Яшин // Особенности деформаций бетона и железобетона и использование ЭВМ для оценки их влияния на поведение конструкций. - М.: Стройиздат, 1969. - С. 38-76.

 Список литературы на английском языке / References in English

1. Harlab V. D. Jenergeticheskaja teorija nelinejnoj polzuchesti i dli-tel'noj prochnosti hrupko razrushajushhihsja materialov (I) [Energy theory of nonlinear creep and long-term strength of brittle materials (I)] / V. D. Harlab // Mehanika sterzhnevyh sistem i sploshnyh sred : mezhvuz. tematich. sb. tr. [Mechanics of rod systems and solid media: Interuniversity thematic collection of works] – L.: LISI. – 1981. - Issue. 14. - P. 11–17. [in Russian]
2. Harlab V. D. Jenergeticheskaja teorija nelinejnoj polzuchesti i dli-tel'noj prochnosti hrupko razrushajushhihsja materialov (II) [Energy theory of nonlinear creep and long-term strength of brittle materials (II)] / V. D. Harlab // Issledovanija po mehanike stroitel'nyh konstrukcij i materialov : mezhvuz. tematich. sb. tr. [Research on the mechanics of building structures and materials: Interuniversity thematic collection of works] – L.: LISI. – 1982. - P. 136–141. [in Russian]
3. Harlab V. D. Jenergeticheskaja teorija nelinejnoj polzuchesti i dli-tel'noj prochnosti hrupko razrushajushhihsja materialov (III) [Energy theory of nonlinear creep and long-term strength of brittle materials (III)] / V. D. Harlab // Issledovanija po teoreticheskim osnovam rascheta stroitel'nyh konstrukcij [Research on the theoretical basis of calculation of building structures: Interuniversity thematic collection of works] – L.: LISI. – 1983. - P. 127–132. [in Russian]
4. Kotov A. A. K teorii polzuchesti i dlitel'noj prochnosti betona [On the theory of creep and long-term strength of concrete] / A. A. Kotov. // Vestnik MGTU [MSTU Bulletin] – 2002. - Vol 5. - № 2. - P. 161–166. [in Russian]
5. Kotov A. A. Teorija deformirovanija i razrushenija hrupkih materialov: proverka po rezul'tatam prostejshih jeksperimentov [Theory of deformation and destruction of brittle materials: verification based on the results of simple experiments] / A. A. Kotov. // Nauka i obrazovanie – 2003 : materialy vserossijskoj nauchno-tehnicheskoj konferencii, Murmansk [Science and education-2003: proceedings of the all-Russian scientific and technical conference, Murmansk] / Murmanskij gos. tehn. un-t [Murmansk state technical University]. – Murmansk, 2003. [in Russian]
6. Jashin A. V. Deformacii betona pod dlitel'nym vozdejstviem vysokih naprjazhenij i ego dlitel'noe soprotivlenie pri szhatii [Concrete deformations under long-term influence of high stresses and its long-term compression resistance] / A. V. Jashin // Osobennosti deformacij betona i zhelezobetona i ispol'zovanie JeVM dlja ocenki ih vlijanija na povedenie konstrukcij [Features of concrete and reinforced concrete deformations and the use of computers to assess their impact on the behavior of structures]. - M.: Strojizdat, 1969. - P. 38-76. [in Russian]