МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОННОГО ПЕРЕНОСА В ЭЛЕМЕНТАХ ФЛЕШ-ПАМЯТИ

МОДЕЛИРОВАНИЕ ПРОСТРАНСТВЕННЫХ ХАРАКТЕРИСТИК ЭЛЕКТРОННОГО ПЕРЕНОСА В ЭЛЕМЕНТАХ ФЛЕШ-ПАМЯТИ

Научная статья

Жевняк О.Г.^1, *, Жевняк Я.О.²

¹ ORCID: 0000-0001-7932-4291;

^{1, 2} Белорусский государственный университет, Минск, Беларусь

* Корреспондирующий автор (Zhevnyakol[at]tut.by)

Аннотация

На основе кинетического метода Монте-Карло проведено численное моделирование электронного переноса в кремниевых короткоканальных МОП-транзисторах с плавающим затвором, являющихся базовым элементом современных микросхем флеш-памяти. С помощью данного моделирования рассчитано влияние затворного напряжения на относительную величину туннельного паразитного тока, возникающего на плавающем затворе, а также среднюю энергию и подвижность электронов в проводящем канале данных транзисторов при разных напряжениях на стоке. Показано, что для исследованных условий это влияние существенно на срединном участке проводящего канала транзистора и снижается у истокового и стокового перехода прибора.

Ключевые слова: флеш-память, МОП-транзистор, туннельный ток, подвижность.

SIMULATION OF ELECTRONIC TRANSFER SPATIAL CHARACTERISTICS IN FLASH MEMORY ELEMENTS

Research article

 Zhevnyak O.G.^1, *, Zhevnyak J.O.²

¹ ORCID: 0000-0001-7932-4291;

^{1, 2}  Belarusian State University, Minsk, Belarus

* Corresponding author (Zhevnyakol[at]tut.by)

Abstract

Based on the kinetic Monte Carlo method, a numerical simulation of electron transport in silicon short-channel floating-gate MOS transistors, which are the basic element of modern flash memory chips, is performed. This simulation is used to calculate the effect of the gate voltage on the relative value of the tunnel parasitic current that occurs on a floating gate, as well as the average energy and mobility of electrons in the conducting channel of these transistors at different drain voltages. It is shown that for the studied conditions, this effect is significant in the middle section of the conducting channel of the transistor and decreases at the source and drain junctions of the device.

Keywords: flash memory, MOS transistor, tunneling current, mobility.

Введение

Уменьшение размеров элементов современных интегральных микросхем, в частности, проводящих каналов МОП-транзисторов, является ключевой тенденцией развития современных флеш-технологий. Повышение емкости микросхем флеш-памяти на основе кремниевых МОП-транзисторов с плавающими затворами накладывает строгие ограничения на величину паразитных туннельных токов, которые будут возникать в этих транзисторах (см., например, [1], [2], [3]). Данные паразитные токи обусловлены туннелированием электронов на плавающий затвор при их дрейфе от истока к стоку транзистора в режиме считывания бита информации. В случае сильного разогрева электронов в результате дрейфа в непосредственной близости от поверхности раздела Si / SiO₂ величина паразитного тока на плавающий затвор может нежелательно возрасти и исказить хранящийся на данном затворе бит информации. Для предотвращения этого необходимо уменьшить вероятность туннелирования, что можно обеспечить, либо снижая возможность разогрева электронов, либо увеличивая степень их отклонения при дрейфе в глубину подложки транзистора — подальше от границы раздела Si / SiO₂ [4]; [5]. 

Методы и принципы исследования

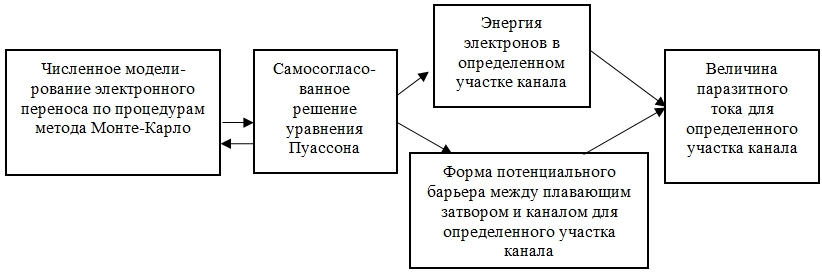
Целью настоящей статьи явилось изучение влияния кинетических характеристик электронного дрейфа в короткоканальных МОП-транзисторах, лежащих в основе современных элементов флеш-памяти, на величину паразитного тока в них. Рассматривалось несколько режимов считывания информации (уровней затворного и стокового напряжения на соответствующих электродах транзистора). Особое внимание уделялось пространственному распределению характеристик в различных участках проводящего канала и их влиянию на величину паразитного тока в этих участках. Данное влияние исследовалось с помощью численного моделирования движения электронов в проводящем канале транзистора методом Монте-Карло вместе с самосогласованным решением уравнения Пуассона с последующим вычислением пространственных распределений величины паразитного туннельного тока на основе решения уравнения Шрёдингера. Алгоритмы численного моделирования методом Монте-Карло приведены в работах [6]; [7], а процедура расчета туннельного тока рассмотрена в работе [8]. На рисунке 1 приведена блок-схема расчета величины паразитного тока в определенном участке проводящего канала.

Рис. 1 – Краткая блок-схема моделирования пространственного распределения величины паразитного тока в элементах флеш-памяти

В результате численного моделирования рассчитывались распределения относительной величины паразитного тока к току стока, а также средних значений энергии и подвижности электронов вдоль проводящего канала от истока (х = 0) к стоку (х = L_ch) при разных значениях напряжения на затворе и стоке. Моделировался МОП-транзистор с плавающим затвором стандартной конструкции, схема которого представлена на рисунке 2. Приведенные ниже результаты моделирования получены для транзистора со следующими конструктивно-технологическими параметрами:

• длина канала L_ch = 0,2 мкм, толщина подзатворного окисла d_ox= 6 нм,
• толщина туннельного окисла d_tun = 2 нм,
• толщина плавающего затвора d_float = 2 нм,
• концентрация донорной примеси в областях истока и стока N_D = 10²⁶ м^–3,
• концентрация акцепторной примеси в подложке N_A = 10²⁴ м^–3,
• глубина залегания истоковой и стоковой областей в подложку d_j = 50 нм.

Основные результаты

На рисунках 3 – 5 приведены полученные в результате моделирования рассчитанные распределения вдоль канала относительной величины паразитного туннельного тока (отношения величины туннельного тока к току стока), а также средних значений энергии и подвижности электронов. Расчеты проводились для двух значений напряжения на стоке V_D = 1 В (кривые 1) и V_D = 3 В (кривые 2), а также на затворе V_G = 1 В (штриховые кривые) и V_G = 3 В (непрерывные кривые).

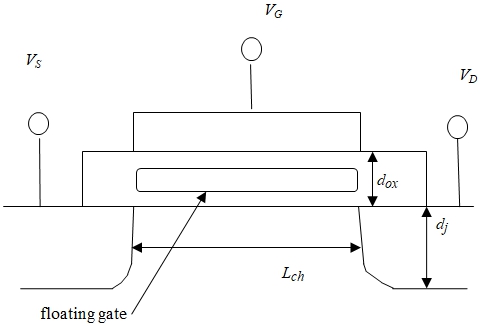
Рис. 2 – Конструкция стандартного МОП-транзистора с плавающим затвором

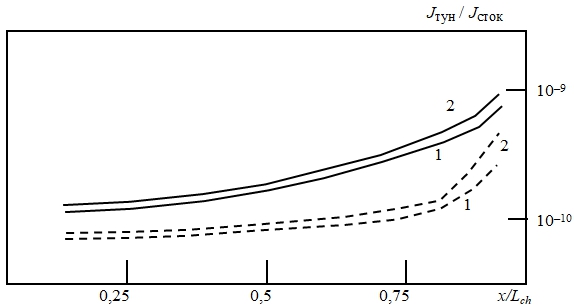
Рис. 3 – Распределения вдоль канала МОП-транзистора относительной величины паразитного тока

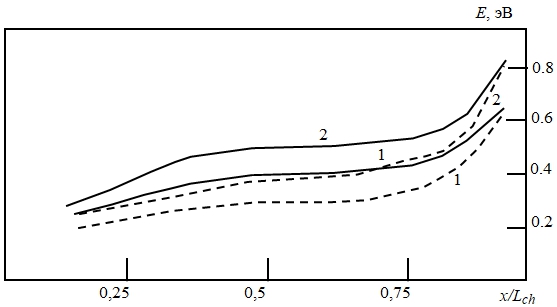
Рис. 4 – Распределения вдоль канала МОП-транзистора средних значений энергии электронов

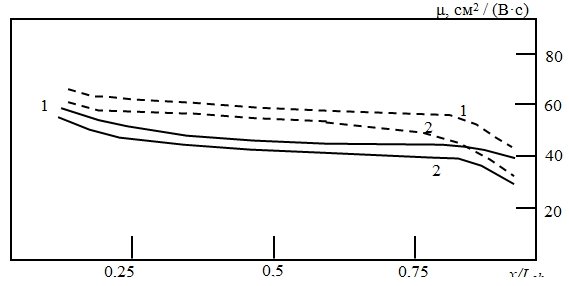
Рис. 5 – Распределения вдоль канала МОП-транзистора средних значений подвижности электронов

 

Полученные распределения позволяют отметить, что влияние затворного напряжения на параметры, характеризующие электронный перенос в рассматриваемом короткоканальном МОП-транзисторе, довольно существенно. Увеличение затворного напряжения приводит к заметному росту относительной величины паразитного тока, что можно объяснить значительным увеличением концентрации электронов в канале. Также с ростом V_G происходит заметное увеличение средней энергии электронов и приблизительно пропорциональное ему уменьшение подвижности электронов. Аналогичное влияние, только в меньшей мере, оказывает и увеличение стокового напряжения.

Анализируя взаимное влияние обоих напряжений, можно отметить, что на начальном (вблизи истока) и конечном (вблизи стока) участках канала влияние затворного напряжения минимально (у стока в бόльшей мере), а для кривых энергии оно почти исчезает — непрерывные и штриховые линии, соответствующие одинаковым значениям V_D, почти совпадают. В то же время в середине канала влияние затворного напряжения максимально — непрерывные и штриховые кривые, соответствующие одинаковым V_D, расходятся на максимальное расстояние.

Для понимания и объяснения отмеченных закономерностей следует иметь в виду два основных фактора влияния затворного напряжения на электрические характеристики короткоканальных МОП-транзисторов [9]; [10]. Повышение затворного напряжения приводит к существенному увеличению концентрации электронов в проводящем канале (в нашем случае максимальная концентрация электронов увеличивается приблизительно от величины N_е = 2,5·10²⁴ м^–3 до N_е = 7·10²⁴ м^–3) и увеличению напряженности поперечной составляющей электрического поля, направленной от поверхности раздела в глубь подложки. В этой связи исчезновение влияния затворного напряжения вблизи стока, очевидно, обусловлено тем, что два указанных фактора в этой области канала фактически нивелируются. Максимальное же действие этих факторов наблюдается в середине проводящего канала исследуемого МОП-транзистора. Причем на всех полученных распределениях можно выделить участок канала прибора с более пологим изменением кривых – от 0,25 до 0,75 х / L_ch. Это и есть область максимального влияния затворного напряжения. 

Заключение

Таким образом, в настоящей работе c помощью численного моделирования методом Монте-Карло проанализировано влияние затворного и стокового напряжения на распределения относительной величины туннельного тока, а также средних значений энергии и подвижности электронов вдоль канала короткоканальных МОП-транзисторов. Показано, что оно существенно и неоднородно почти вдоль всего проводящего канала транзистора и только вблизи стока практически исчезает.

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Gerardi C. Nanocrystal Memory Cell Integration in a Stand-Alone 16-Mb NOR Flash Device / C. Gerardi, V. Ancarani, R. Portoghese et al. // IEEE Trans. Electron Devices. – 2007. – Vol. 54. – No 6. – P. 1376–1383.
2. Govoreanu D. Performance and Reliability of HfAlO_x-based Interpolary Dielectrics for Floating-Gate Flash Memory / D. Govoreanu, D. Wellekens, L. Haspeslagh et al. // Solid-State Electron. – 2008. – Vol. 52. – Iss. 4. – P. 557–563.
3. De Salvo B. Silicon Non-Volatile Memories: paths of innovation / B. De Salvo. – London: Wiley-ISTE Ltd, 2009. – 256 p.
4. Fiegna C. Scaling the MOS Transistor Below 0.1 μm: Methodology, Device Structures, and Technology Requirements / C. Fiegna, H. Iwai, T. Wada et al. // IEEE Trans. Electron Dev. – 1994. – Vol. 41. – No 6. – P. 941–951.
5. Iwai H. Technology toward low power / low voltage and scaling of MOSFETs / H. Iwai, H. S. Momose // Microelectron. Engineer. – 1997. – Vol. 39. – No 1. – P.7–30.
6. Борздов В. М. Моделирование методом Монте-Карло приборных структур интегральной электроники / В. М. Борздов, О. Г. Жевняк, Ф. Ф. Комаров и др. – Минск: БГУ, 2007. – 175 с.
7. Zhevnyak O. Temperature effect on electron transport in conventional short channel MOSFETs: Monte Carlo simulation / O. Zhevnyak // Proc. SPIE. – 2008. – Vol. 7025. – P. 1M-1–8.
8. Жевняк О. Г. Моделирование туннельного тока в элементах флеш-памяти / О. Г. Жевняк // Международный научно-исследовательский журнал. – 2015. – Вып. 9. – Ч. 3. – С. 49–53.
9. Zhevnyak O. Monte Carlo study of influence of channel length and depth on electron transport in SOI MOSFETs / O. Zhevnyak, V. Borzdov, A. Borzdov et al. // Proc. SPIE. – 2008. – Vol. 7025. – P. 1L-1–8.
10. Жевняк О. Г. Моделирование методом Монте-Карло влияния глубины залегания стока на перенос электронов и ток стока в субмикронных МОП-транзисторах / О. Г. Жевняк, И. М. Шевкун // Вестник Белгосуниверситета. Сер. Физ. Мат. Инф. – 2014. – №3. – С. 38–40.

Список литературы на английском языке / References in English

1. Gerardi C. Nanocrystal Memory Cell Integration in a Stand-Alone 16-Mb NOR Flash Device / C. Gerardi, V. Ancarani, R. Portoghese et al. // IEEE Trans. Electron Devices. – 2007. – Vol. 54. – No 6. – P. 1376–1383.
2. Govoreanu D. Performance and Reliability of HfAlO_x-based Interpolary Dielectrics for Floating-Gate Flash Memory / D. Govoreanu, D. Wellekens, L. Haspeslagh et al. // Solid-State Electron. – 2008. – Vol. 52. – Iss. 4. – P. 557–563.
3. De Salvo B. Silicon Non-Volatile Memories: paths of innovation / B. De Salvo. – London: Wiley-ISTE Ltd, 2009. – 256 p.
4. Fiegna C. Scaling the MOS Transistor Below 0.1 μm: Methodology, Device Structures, and Technology Requirements / C. Fiegna, H. Iwai, T. Wada et al. // IEEE Trans. Electron Dev. – 1994. – Vol. 41. – No 6. – P. 941–951.
5. Iwai H. Technology toward low power / low voltage and scaling of MOSFETs / H. Iwai, H. S. Momose // Microelectron. Engineer. – 1997. – Vol. 39. – No 1. – P.7–30.
6. Borzdov V. M. Modelirovanije metodom Monte Carlo pribornych struktur integral’noj elektroniki [Monte Carlo simulation of device structures of integral electronics] / V. M. Borzdov, O. G. Zhevnyak, F. F. Komarov et al. – Minsk: BSU, 2007. – 175 p. [in Russian]
7. Zhevnyak O. Temperature effect on electron transport in conventional short channel MOSFETs: Monte Carlo simulation / O. Zhevnyak // Proc. SPIE. – 2008. – Vol. 7025. – P. 1M-1–8.
8. Zhevnyak O. G. Modelirovanije tunnel’nogo toka v elementach flesh-pamjati [Simulation of tunnel current in flash-memory elements] / O. G. Zhevnyak // International Research Journal. – 2015. – Iss. 9. – Pt. 3. – P. 49–53. [in Russian]
9. Zhevnyak O. Monte Carlo study of influence of channel length and depth on electron transport in SOI MOSFETs / O. Zhevnyak, V. Borzdov, A. Borzdov et al. // Proc. SPIE. – 2008. – Vol. 7025. – P. 1L-1–8.
10. Zhevnyak O. G. Modelirovanije metodom Monte Carlo vlijanija glubiny zaleganija stoka na perenos elektronov i tok stoka v submikronnych MOP-tranzistorach [Monte Carlo simulation of drain deepness effect on electron transport as well as drain current in submicron MOS-transistors] / O. G. Zhevnyak, I. M. Shevkun // Journal of the Belarusian State University. Physics. – 2014. – No 3. – P. 38–40. [in Russian]