Наши журналы
Опубликовать статью Вход и регистрация
Расширенный поиск
Разделы статьи

ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В АВТОНОМНОЙ СИСТЕМЕ С ЭНЕРГОСНАБЖЕНИЕМ ОТ ВИЭ

Научная статья
Петров Ю.С.
Музаев А.К.
DOI:
https://doi.org/10.23670/IRJ.2020.100.10.006
Выпуск: № 10 (100), 2020
Опубликована:
2020/10/16
PDF

ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В АВТОНОМНОЙ СИСТЕМЕ С ЭНЕРГОСНАБЖЕНИЕМ ОТ ВИЭ

Научная статья

Петров Ю.С.1, Музаев А.К.2, *

1, 2 Северо-Кавказский горно-металлургический институт (государственный технологический институт), Владикавказ, Россия

* Корреспондирующий автор (alexandr.muzaev[at]mail.ru)

Аннотация

В статье рассмотрены энергетические соотношения в автономной системе энергоснабжения от возобновляемых источников энергии. Для решения уравнения энергетического баланса, которое является вероятностным, применимы методы решения: переход к математическим ожиданиям и более точный – метод Монте-Карло. Рассмотрено более подробно применение метода Монте-Карло, например, для наличия в установке преобразователя только источников электрической энергии. Для расчёта универсальной энергетической установки и определения параметров накопительного устройства необходимо определить выходную мощность с учётом стохастического характера её изменения. Предложен алгоритм реализации статистического моделирования изменения выходной мощности установки в соответствии со случайно изменяющимися значениями выходных мощностей, входящих в состав установки, генераторов.

Ключевые слова: возобновляемые источники энергии; автономная система энергоснабжения; энергетические соотношения.

ENERGY RELATION IN AUTONOMOUS SYSTEM WITH ENERGY SUPPLY FROM RES

Research article

Petrov Yu.S.1, Muzaev A.K.2, *

1, 2 North Caucasian Mining and Metallurgical Institute (State Technological Institute), Vladikavkaz, Russia

* Corresponding author (alexandr.muzaev[at]mail.ru)

Abstract

The paper discusses the energy ratios in an autonomous power supply system powered from renewable energy sources (RES). The following solution methods can be applied to solve this probabilistic energy balance equation: the transition to mathematical expectations and, more accurately, the Monte Carlo method. The application of the Monte Carlo method is considered in detail, for example, for the presence of only sources of electrical energy in the converter installation. To calculate the universal power plant and determine the parameters of the storage device, it is necessary to determine the output power taking into account the stochastic nature of its change. The authors propose the algorithm for the implementation of statistical modeling of changes in the output power of the unit in accordance with randomly varying values of the output powers of the installation generators.

Keywords: renewable energy sources; autonomous power supply system; energy relations.

Цель: установить функционально и проанализировать энергетические соотношения в автономной системе с энергоснабжением от ВИЭ.

Задача: вывести математические зависимости, описывающие энергетический баланс в автономной системе генератор – накопитель – потребитель, с генерацией электрической энергии от ВИЭ; дать методику анализа энергетического баланса с учётом стохастического баланса с учётом стохастического характера изменения его составляющих.

Научная новизна: дана методика вероятностного анализа уравнения энергетического баланса в автономной системе энергоснабжения от ВИЭ с применением статистического моделирования.

Введение

Математической основой энергетического соотношения в автономной системе с энергоснабжением от ВИЭ [1], [2], [9] является баланс между произведённой от ВИЭ и израсходованной потребителями энергией.

 

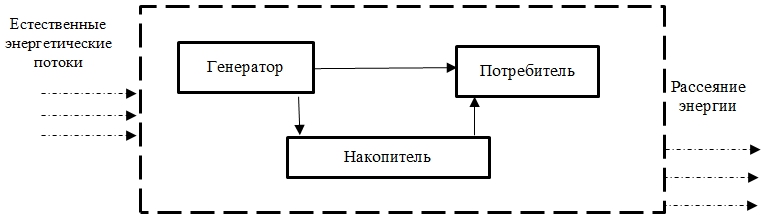27-10-2020 17-18-13 Рис. 1 – Автономная система с энергоснабжением от ВИЭ

На рис. 1 схематически изображена автономная система с энергоснабжением от ВИЭ. Уравнение энергетического баланса для определённого промежутка времени в общем случае можно записать, используя средние значения величин, в виде равенства:

∑Si = ∑Sпотр ± Sнк (1)

где ∑Si – суммарная мощность преобразователей генерирующей составляющей общей системы;

∑Sпотр – суммарная потребляемая мощность;

Sнк – мощность, передаваемая в накопительное устройство.

При избытке генерируемой мощности часть её передаётся в накопительное устройство, и оно работает в режиме потребителя (знак «+»). При недостатке генерируемой мощности (по сравнению с требуемой для нормальной работы потребителей) она поступает к накопительному устройству в систему потребления и мощность Sнк имеет знак «-». Формально слагаемое «–Sнк» можно перенести в левую часть уравнения со знаком «+», что соответствует работе накопительного устройства в режиме генератора, т.е. в режиме передачи мощности потребителю.

Методы и принципы исследования

Как уже указывается, выражение (1) записано для средних за определённое время величин. Более корректным с математической точки зрения будут выражения, записанные для мгновенных значений мощности:

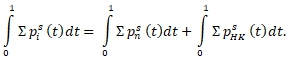27-10-2020 17-18-29       (2)

Уравнение (2) имеет две существенные особенности. Во-первых, оно может содержать качественно разнородные величины (электрические, тепловые и механические генераторы и потребители). Для наиболее распространённого варианта – наличие электро- и термогенераторов и потребителей и учитывая, что избыток электроэнергии может частично преобразоваться в тепло и передаваться в тепловой накопитель. Уравнение (2) можно переписать в виде:

 WГ + QГ = WП ± WH ± QП ± QH, (3)

где WГ, WП, WH- электрическая энергия – генерируемая, потребляемая и накапливаемая соответственно;

QГ, QП, QH – тепловая энергия – генерируемая, потребляемая и накапливаемая соответственно.

Во-вторых, строго говоря уравнение (2) является вероятностным, т.к. содержащиеся в нём величины являются в общем случае случайными: производительность установки, работающей на ВИЭ [7], [8], [10], зависит от целого ряда случайных факторов, в частности, от параметров естественных энергетических потоков; параметров потребителей, например, в жилом доме, а также постоянно меняющихся потребителей и т.д.

Мощность, отдаваемая накопителю, зависит от соотношения генерируемой и потребляемой мощностей и также является величиной случайной.

Таким образом, уравнение энергетического баланса (2) является вероятностным, а, следовательно, к нему применимы методы решения вероятных уравнений: переход к математическим ожиданиям (уравнение 1) и более точный – метод Монте-Карло.

Основные результаты и обсуждения

Рассмотрим более подробно применение последнего метода, например, для наличия в установке преобразователя только источников электрической энергии [3], [4].

Суммарная мощность S∑ установки (преобразовательного комплекса) равна

S∑ = S1 + S2 + … + Sn = F(S) (4)

где S1,S2 … Sn – выходные мощности соответственно 1-го, 2-го …n-го генераторов (например, ветро-, гелио-, гидро- электрогенераторов).

Выходная мощность является случайной величиной, т.к. равна сумме случайных величин, изменяющихся по различным законам вследствие влияния случайных факторов (скорость и направление ветра, интенсивность солнечного облучения, уровень и напор воды в горной реке и т.п.).

Для расчёта универсальной энергетической установки в части определения параметров накопительного устройства необходимо прежде всего определить выходную мощность и закон её изменения [5], [6]. Эти задачи можно решить, реализуя статистическое моделирование (метод Монте-Карло).

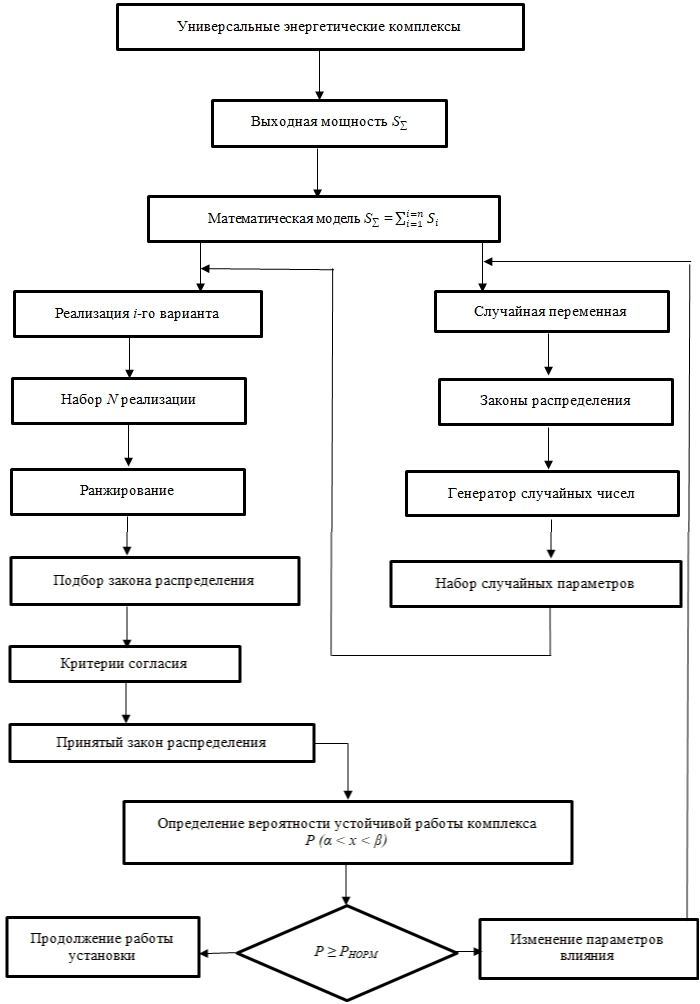
Алгоритм реализации статистического моделирования изменения выходной мощности S∑ установки в соответствии со случайно изменяющимися по разным законам значениями выходных мощностей S1,S2 … Sn отдельных, входящих в состав установки, генераторов, показан на рис. 2.

m_merged55

Рис. 2 – Алгоритм вероятностного анализа изменения выходной мощности универсальных энергетических комплексов

 

Рабочее состояние объекта (универсального энергетического комплекса) определяется сочетанием его постоянных – конструктивных параметров всех составляющих комплекса и изменяющихся – случайных параметров, влияющих на его работу и определяемых случайными факторами. Например, ветрогенератор, скорость ветра в общем случае может считаться случайной величиной и, следовательно, случайной величиной будет мощность ветрогенератора (в математическое выражение которой, как известно, скорость ветра входит в третьей степени).

Перед началом вычислительных операций, реализующих статистическое моделирование, необходимо задать законы распределения случайных величин (S1,S2 … Sn), входящих в формулу выходной мощности:

 

27-10-2020 17-22-28     (5)

Законы распределения мощностей Si отдельных генераторов комплекса устанавливаются на основании экспериментальных данных и ретроспективного анализа.

Далее по случайной выборке мощностей генераторов, составленной в соответствии с их законами распределения, с помощью генератора случайных чисел вычисляется выходная мощность по формуле (5) – «i»-ая реализация процесса статистического моделирования.

Таким образом, производится набор N реализаций (обычно 103 ≤ N ≤ 104).

Набранный массив данных ранжируется, при необходимости выводятся на печать гистограммы, устанавливается закон распределения мощности как случайной величины.

По установленному закону распределения определяется вероятность попадания значения выходной мощности в заданный интервал Р (α < х < β), где α и β – минимальное и максимальное допустимые (заданные) значения мощности соответственно, обеспечивающие нормальную работу установки.

Если выполняется условие Р ≤ РНОРМ, где РНОРМ – нормированное значение вероятности, обеспечивающее штатную работу комплекса, то работа комплекса в данных условиях может быть продолжена; если это неравенство не выполняется, то следует принять меры по уменьшению влияния случайных факторов.

Заключение

Вероятностный анализ изменения выходной мощности универсального энергетического комплекса вследствие влияния случайных факторов позволяет определить условия устойчивой работы комплекса, конкретизировать необходимые параметры накопительного устройства, оценить надёжность работы энергосистемы.

Конфликт интересов Не указан. Conflict of Interest None declared.

Список литературы / References

  1. Ресурсы и эффективность использования возобновляемых источников энергии в России: [Монография] / [П.П. Безруких, Ю.Д. Арбузов, Г.А. Борисов и др.]; Под общ. ред. П.П. Безруких; М-во энергетики Рос. Федерации [и др.]. - СПб.: Наука, 2002. – 313 с.
  2. Альтернативные источники энергии и энергосбережение. М.: Наука и техника, 2014. – 320 с.
  3. Ермаков С.М. Метод Монте-Карло в вычислительной математике: ввод. Курс / С.М. Ермаков. М.; СПб.: Бином. Лаб. Знаний: Нев. Диалект, 2009, 192 с.
  4. Войтишек А.В. Дополнительные сведения о численном моделировании случайных элементов: учеб. пособие / А.В. Войтишек. Новосибирск: НГУ, 2007, 92 с.
  5. Зорина И.Ю. Расчёт мощности комплексной автономной установки преобразования возобновляемой энергии / И.Ю. Зорина, М.К. Хадиков, А.М. Дзгоев // Вестник МАНЭБ, Т. 21, №3 – 2016, 89с.
  6. Алборов И.Д. Повышение эффективности преобразователей возобновляемой энергии в электрическую / И.Д. Алборов, Ю.С. Петров, И.Ю. Зорина // Вестник МАНЭБ, т. 19, №4 – 2014, 53 с.
  7. Петров Ю.С. Ветрогелиоустановка, патент № 188444 / Ю.С. Петров, М.К. Хадиков, А.А. Соколов, А.К Музаев. опубликован 12.04.2019, бюллетень № 11.
  8. Петров Ю.С. Устройство автономного освещения дорожного разделительного барьера, патент № 196315 / Ю.С. Петров, М.К. Хадиков, А.К Музаев., опубликован 25.02.2020 г, бюллетень № 6.
  9. Велькин В.И. Методология расчёта комплексных систем ВИЭ для использования на автономных объектах: монография / В.И. Велькин. Екатеринбург: Изд-во УрФУ, 2015 – 226 с.
  10. Стимулирование освоения нетрадиционных возобновляемых источников энергии: мировые тенденции и Россия / А. Тарасов // Экономические науки. – 2009 - № 5 – С. 176 – 178.

Список литературы на английском языке / References in English

  1. Resursy i effektivnost' ispol'zovaniya vozobnovlyayemykh istochnikov energii v Rossii [Resources and efficiency of using renewable energy sources in Russia]: [Monograph] / P.P. Bezrukikh, Yu.D. Arbuzov, G.A. Borisov et. al.; Ed. by P.P. Armless; Energy Ministry Ros. Federation– SPb.: Nauka, 2002. – 313. [in Russian]
  2. Al'ternativnyye istochniki energii i energosberezheniye [Alternative energy sources and energy saving]. M.: Science and technology, 2014. – 320 p. [in Russian]
  3. Ermakov S.M. Metod Monte-Karlo v vychislitel'noy matematike: vvod. kurs [Monte Carlo method in computational mathematics: Start. Course] / S.M. Ermakov. M.; SPb.: Binom. Lab. Knowledge: Nev. Dialect, 2009, 192 p. [in Russian]
  4. Voytishek A.V. Dopolnitel'nyye svedeniya o chislennom modelirovanii sluchaynykh elementov [For more information about numerical modeling of random elements]: textbook. Manual / A.V. Voytishek. Novosibirsk: NSU, 2007, 92 p. [in Russian]
  5. Zorina I.Yu. Raschot moshchnosti kompleksnoy avtonomnoy ustanovki preobrazovaniya vozobnovlyayemoy energii [Calculation of capacity of complex autonomous installation for converting renewable energy] / I.Yu. Zorina, M.K. Khadikov, A.M. Dzgoev // Vestnik MANEB, V. 21, No. 3 – 2016, 89p. [in Russian]
  6. Alborov I.D. Povysheniye effektivnosti preobrazovateley vozobnovlyayemoy energii v elektricheskuyu [Improving efficiency of converters of renewable energy into electricity] / I.D. Alborov, Yu.S. Petrov, I.Yu. Zorina // Vestnik MANEB, v. 19, No. 4 – 2014, 53 p. [in Russian]
  7. Petrov Yu.S. Vetrogelioustanovka [Wind turbine plant] / Yu.S. Petrov, M.K. Khadikov, A.A. Sokolov, A.K. Muzaev. Patent No. 188444, published on 12.04.2019, bulletin No. 11. [in Russian]
  8. Petrov Yu.S. Ustroystvo avtonomnogo osveshcheniya dorozhnogo razdelitel'nogo bar'yera [Device for autonomous lighting of road separation barrier] / / Yu.S. Petrov, M.K. Khadikov, A.K. Muzaev. Patent No. 196315, published on February 25, 2020, bulletin No. 6. [in Russian]
  9. Vel'kin V.I. Metodologiya raschota kompleksnykh sistem VIE dlya ispol'zovaniya na avtonomnykh ob"yektakh: monografiya [Methodology for calculating complex RES systems for use at autonomous facilities: monograph]. / V.I. Vel'kin / Yekaterinburg: UrFU Publishing House, 2015 – 226 p. [in Russian]
  10. Stimulirovaniye osvoyeniya netraditsionnykh vozobnovlyayemykh istochnikov energii: mirovyye tendentsii i Rossiya [Stimulating development of non-traditional renewable energy sources: global trends and Russia] / A. Tarasov // Economic sciences. – 2009 – No. 5 – P. 176 – 178. [in Russian]