АНАЛИЗ ФИЛЬТРАЦИОННЫХ РЕЖИМОВ ИЗ-ПОД ВОДОБОЯ С ИСПОЛЬЗОВАНИЕМ ГЕОМЕМБРАНЫ В ОСНОВАНИИ

АНАЛИЗ ФИЛЬТРАЦИОННЫХ РЕЖИМОВ ИЗ-ПОД ВОДОБОЯ С ИСПОЛЬЗОВАНИЕМ ГЕОМЕМБРАНЫ В ОСНОВАНИИ

Научная статья

Атабиев У.И.^1, *, Тезадова О.А.²

¹ ORCID: 0000-0002-1825-0097;

¹ Российский государственный аграрный университет им. К.А. Тимирязева, Москва, Россия;

² Российский университет дружбы народов, Москва, Россия

* Корреспондирующий автор (a_omar[at]mail.ru)

Аннотация

В данной статье описана проблема нарушения фильтрационных режимов работы. Проведен фильтрационный расчет и анализ противофильтрационной геомембраны подземного контура гидротехнических сооружений. Для определения коэффициентов сопротивления области фильтрации противофильтрационной геомембраны в основании подземного контура, преобразовано комформное отображение области коэффициента сопротивления (ζ), на комплексный потенциал фильтрации. Рассчитан коэффициент сопротивления. при использовании аналитической связи, расчетных схем противофильтрационного экрана, в основании с проницаемым креплением, с любой другой областью простейшего очертания с известными. Произведя простые преобразования, принимая последовательно, что , получим соответственно , иcходя из этого максимальный градиент напора, найдём прировняв первую производную к нулю. Полученная зависимость имеет такую же структуру, что и известная формула Р.Р. Чугаева для выходного уступа и шпунта, полученная им на основании гидромеханического решения С.Н. Нумерова. При практических соотношениях , коэффициент сопротивления на выходе из-под горизонтального экрана будет на 10% ниже, чем для уступа. Уменьшился напор в конце выработки подземного контура, до  = 43%, при этом - выходные градиенты снижаются на =30...50%.

Ключевые слова: фильтрационный поток, шпунт, обтекание, завеса, геомембрана, горизонтальный экран, гидротехнические сооружения.

ANALYSIS OF FILTER MODES FROM WATER JET WITH THE USE OF GEOMEMBRANE IN ITS BASIS

Research article

Atabiev U.I.^1, *, Tezadova O.A.²

¹ ORCID: 0000-0002-1825-0097;

¹ Moscow Timiryazev Agricultural Academy, Moscow, Russia;

² Peoples' Friendship University of Russia, Moscow, Russia

* Corresponding author (a_omar[at]mail.ru)

Abstract

This paper considers the problem of violation of filtration modes. The authors carried out filtration calculation and the analysis of the anti-filtration geomembrane of the underground water circuit of hydraulic structures. A conformal mapping of the region resistance coefficient (ζ) to the complex filtration potential was converted to determine the resistance coefficients of the filtration area of the antifiltration geomembrane at the base of the underground water circuit. The resistance coefficient was calculated for the case of analytical connection, design schemes of an anti-filter screen were used, in the base with permeable fastening, with any other area of the simplest outline with the known ones. Performing simple transformations, assuming successively that , we obtain , respectively, and proceeding from this the maximum pressure gradient, we find that the first derivative is equal to zero. The resulting dependence has the same structure as the well-known R.R. Chugaev’s formula for the output ledge and channel, obtained by him based on the hydromechanical solution of S.N. Numerov. With practical ratios  the resistance coefficient at the output from the horizontal screen will be 10% lower than for the ledge. The pressure at the end of the underground circuit development decreased to  = 43%, while the output gradients decrease by  = 30 ... 50%.

Keywords: filtration flow, channel, flow around, curtain, geomembrane, horizontal screen, hydraulic structures.

Введение

Применение синтетических полимерных материалов в гидротехническом строительстве и строительстве дренажных (противофильтрационных) элементов началось еще в первой половине двадцатого века. На начальном этапе использования данных материалов это были тонкие, толщиной 0,1-0,5 мм полиэтиленовые и поливинилхлоридные пленки. В ходе развития технологии производства, качества синтетики, началось изготовление и других материалов. На данный момент полимерные материалы обладают рядом существенных преимуществ перед другими материалами. Они воспринимают значительные растягивающие напряжения, сохраняют прочность даже при больших деформациях, однородны по своему качеству, долговечны, технологичны и эффективны для применения в гидротехническом строительстве. В настоящее время практически все эти листовые материалы и конструкции из них, предназначенные для устройства противофильтрационных элементов различных сооружений, называют «геомембраны».

Рис. 1 – Виды геомембраны

 

Подземный контур такого водобоя формируется горизонтальным полимерным экраном, пригруженным слоем местного грунта, смыв которого предотвращается защитным креплением. Будем полагать, что в основании крепления дна нижнего бьефа располагается пластовый дренаж. Тогда область фильтрации при выходе потока будет иметь вид как на (рис 2а). Интеграл Кристоффеля-Шварца [1], отображающий область комплексного переменного z=х + iy на каноническую полуплоскость ζ+ in (рис. 2б), имеет вид [2]

     (1) Конформное отображение области £ на комплексный потенциал фильтрации (рис.2 в) осуществим следующим образом:     (2) Функция обратная (2)

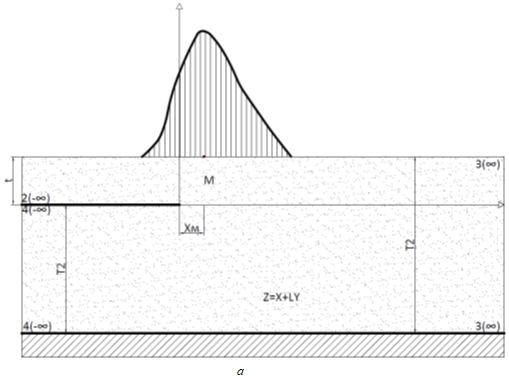
Рис. 2 – Схема к расчету противофильтрационного экрана в основании флютбета с проницаемым креплением.

а – Область фильтрации при выходе потока из подземного контура водобоя с полимерным экраном и пластовым дренажем

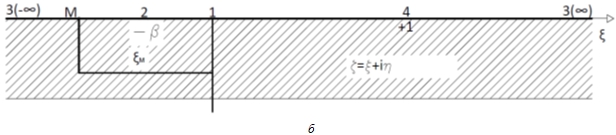
Рис. 2 – Схема к расчету противофильтрационного экрана в основании флютбета с проницаемым креплением.

б – Область комплексного переменного z=х + iy на каноническую полуплоскость ζ+in

 

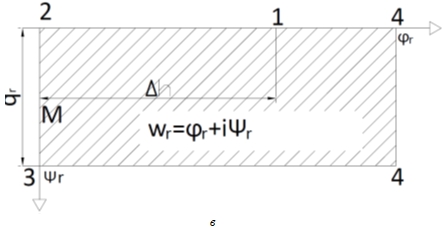
Рис. 2 – Схема к расчету противофильтрационного экрана в основании флютбета с проницаемым креплением.

в – Конформное отображение области £ на комплексный потенциал фильтрации

 

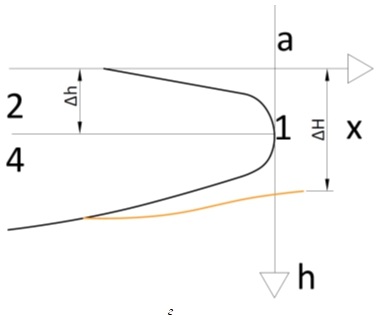
Рис. 2 – Схема к расчету противофильтрационного экрана в основании флютбета с проницаемым креплением.

г – Параметр асимптоты Δh

 

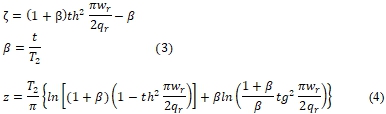
Методы и принципы исследования

Составим из (4) уравнение напоров  и, определив параметр ее асимптоты ∆h (рис.1г) как в [2], [3], найдем из соотношения  формулу для коэффициента сопротивления выходного фрагмента.

    (5)

Комплексный градиент фильтрации определится после того как (4) продифференцируем по w_r

    (6)

Затем принимаем , получим выходные градиенты по линии 2-3

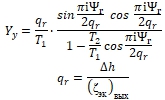    (7)

Пьезометрический напор на конце экрана в точке 1 определится из (2) при .

    (8)

Функция тока  может быть определена из (4) при 

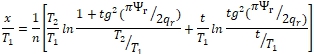   (9)

Принимая последовательно в (9) . Тогда легко убедится в точках нижнего бьефа 2 и 3 согласно (7) будем иметь . Максимально выходной градиент найдем, если приравняем первую производную к (7) нулю.

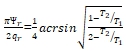  (10)

Подставив (10) и (7), получим

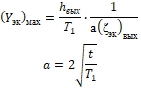   (11)

Получаем в результате, что зависимость (11) имеет такую же структуру, что и известная формула Р.Р. Чугаева [4] для выходного уступа и шпунта, полученная им на основании гидромеханического решения С.Н. Нумерова [3]. Точку М выхода  найдем из (8) с учетом (9)

  (12)

По формулам (7), (9), заданных в параметрическом виде , построены графики выходных градиентов (рис. 3), имеющие куполообразное очертание.

Сопоставим фильтрационные характеристики (5), (8) и (11) иссле-дованного выходного элемента с равновеликим по заглублению t в грунтовое основание уступом [3], [4]

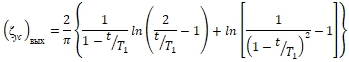   (13)

 

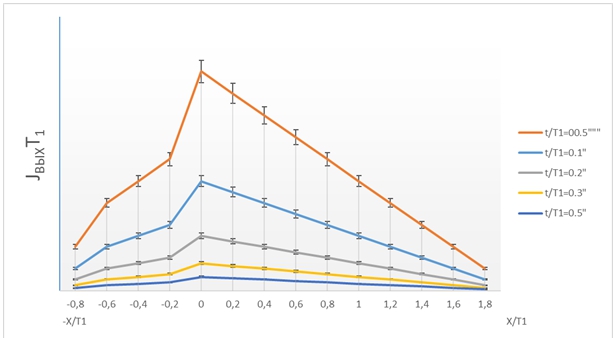
Рис. 3 – График приведенных выходных градиентов

 

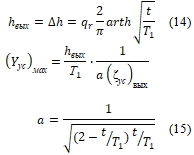
Сравнение показывает (рис. 3), что при практических соотношениях  коэффициент сопротивления на выходе из-под горизонтального экрана будет на 10% и менее ниже , чем для уступа. Это обуславливает уменьшение напоров в конце подземного контура до  , но особенно важно то, что выходные градиенты снижаются на  =40...55%.

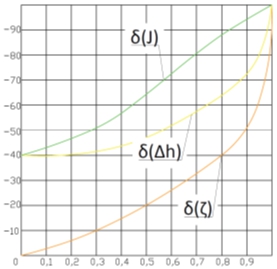
Рис. 4 – График сопоставления фильтрационных характеристик противофильтрационного экрана и уступа

 

Заключение

1.Полученная зависимость имеет такую же структуру, что и формула Р.Р. Чугаева.

2.При практических соотношениях,  коэффициент сопротивления на выходе из-под горизонтального экрана будет на 10% ниже, чем для уступа.

3.Уменьшение напора в конце подземного контура до , но особенно важным является то, что выходные градиенты снижаются на =40...55%.

4.Тип, вид и состав геомембранной основы подбирается исходя из инженерно-геологических характеристик основания контура, изменение характеристик геомембранной основы не влечет за собой значительных изменений в расчетах.

5.Применение геомембраны в основании способствует снижению входных градиентов и уменьшению фильтрационного напора, снижение вероятности суффозии в основании.

Конфликт интересов Не указан.

Conflict of Interest None declared.

 

Список литературы / References

1. Лаврентьев М.А. Методы теории функций комплексного переменного / Лаврентьев М.А., Шабат В.Б. – М.: Наука, 1973. 736 с.
2. Бурдинский В.Н. Определение коэффициента сопротивления входно¬го элемента пленочного понура / Бурдинский В.Н. // Материалы научно- практической конференции Кабардино-Балкарской государственной сельскохозяйственной академии (Технические науки. Вып. 2).– Нальчик:КБГСА, 1996. – С.225-228.
3. Аравин В.Й. Теория движения жидкостей и газов в недеформируемой пористой среде / Аравин В.Й., Нумеров С.Н. – М.: Гостехиздат, 1953. – 616 с.
4. Чугаев Р.Р. Подземный контур гидротехнических сооружений / Чугаев Р.Р. – Л.: Энергия, 1974. – 237 с.
5. Веригин Н.Н. Фильтрация в основании плотин с наклонными завесами и шпунтами / Веригин Н.Н. // Гидротехническое строительство. – 1940.– №2. –131 с.
6. Дегтярь Б.Г. Гидротехнический расчет плотины с наклонным шпунтом при Т < ∞ / Дегтярь Б.Г. / Республиканский межведомственный научно –технический сб., вып.18. // Мелиорация и водное хозяйство. – Киев: Урожай, 1970. 183 с.
7. Фильчаков П.Ф. Теория фильтрации под гидротехническими сооружениям.т.2 / Фильчаков П.Ф. – Киев: Изд. АНУССР, 1960. –123 с.
8. Лаврентьев М.А. Методы теории функции комплексного переменного / Лаврентьев М.А., Шабат В.Б. – М: Наука, 1973. –736 с.
9. Булычев Н.С. Механика подземных сооружний / Булычев Н.С.. – М.: Недра, 1994
10. Гидротехнические сооружения / Под. ред. Г.М. Каганова. Т.2, М.: Энергоатомиздат, 1994. – 464 с.

Список литературы на английском языке / References in English

1. Lavrentiev M.A. Metody teorii funkcij kompleksnogo peremennogo [Methods of the theory of functions of a complex variable] / Lavrentiev M.A., Shabat V.B. – Moscow: Nauka, 1973. 736 p. [in Russian]
2. Burdinsky V.N. Opredelenie koefficienta soprotivleniya vhodnogo elementa plenochnogo ponura [Determination of the coefficient of resistance of the input element of the film circuit] / Burdinsky V. N. / Materials of the scientific and practical conference of the Kabardino-Balkar state agricultural Academy (Technical Sciences. Vol. 2). – Nalchik: CBGS, 1996. - P. 225-228. [in Russian]
3. Aravin V.Th. Teoriya dvizheniya zhidkostej i gazov v nedeformiruemoj poristoj srede [Theory of motion of liquids and gases in a non-deformable porous medium] / Aravin V. Th., Numerov S. N. – Moscow: Gostekhizdat, 1953. – 616 p. [in Russian]
4. Chugaev R.R. Podzemnyj kontur gidrotekhnicheskih sooruzhenij [Underground contour of hydraulic structures] / Chugaev R.R. – L.: Energy, 1974. – 237 p.
5. Verigin N.N. Filtraciya v osnovanii plotin s naklonnymi zavesami i shpuntami [Filtration at the base of dams with inclined curtains and dowels] / Verigin N. N. // Hydraulic engineering. - 1940.- No. 2. - 131 p. [in Russian]
6. Degtyar B.G. Gidrotekhnicheskij raschet plotiny s naklonnym shpuntom pri T < ∞ [Hydrotechnical calculation of a dam with an inclined tongue at T < ∞] / Degtyar B.G. / Republican interdepartmental scientific and technical Council, vol.18. // Land reclamation and water management. – Kiev: Vintage, 1970. 183 p. [in Russian]
7. Filchakov P.F. Teoriya filtracii pod gidrotekhnicheskimi sooruzheniyam.t.2 [Theory of filtration under hydraulic structures.vol. 2] / Filchakov P.F. – Kiev: Ed. ANOSR, 1960. - 123 p. [in Russian]
8. Lavrentiev M.A. Metody teorii funkcii kompleksnogo peremennogo [Methods of the theory of the function of a complex variable] / Lavrentiev M. A., Shabat V. B. – M: Science, 1973. - 736 p. [in Russian]
9. Bulychev N.S. Mekhanika podzemnyh sooruzhnij [Mechanics of underground structures] / Bulychev N. S. – Moscow: Nedra, 1994[in Russian]
10. Gidrotekhnicheskie sooruzheniya [Hydraulic structures] / Edited by G. M. Kaganov Vol. 2, – Moscow: Energoatomizdat, 1994. – 464 p. [in Russian]