АНАЛИЗ МЕТОДОВ РАСЧЕТА БИТОВОЙ ВЕРОЯТНОСТИ ОШИБКИ ПРИ КОГЕРЕНТНОМ ПРИЕМЕ СИГНАЛОВ С M-ИЧНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ

АНАЛИЗ МЕТОДОВ РАСЧЕТА БИТОВОЙ ВЕРОЯТНОСТИ ОШИБКИ ПРИ КОГЕРЕНТНОМ ПРИЕМЕ СИГНАЛОВ С M-ИЧНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ

Научная статья

Зубарев А.Е.^1, *, Позов А.В.², Приходько А.И.³

¹ ORCID: 0000-0003-0615-3414;

² ORCID: 0000-0001-6377-0756;

³ ORCID: 0000-0003-0108-8238;

^{1, 2, 3} Кубанский государственный университет, Краснодар, Россия

* Корреспондирующий автор (shorshett1708919[at]yandex.ru)

Аннотация

В современных и перспективных цифровых телекоммуникационных системах находят широкое применение сигналы с M-ичной фазовой манипуляцией. В статье рассмотрены различные методы расчета битовой вероятности ошибки при когерентном приеме сигналов с M-ичной фазовой манипуляцией в канале связи с постоянными параметрами и аддитивным белым гауссовским шумом. Поведены расчеты битовой вероятности ошибки по точным и приближенным формулам. Обоснованы рекомендации по выбору приближенных формул для оценки битовой вероятности ошибки.

Ключевые слова: M-ичная фазовая манипуляция, сигнальное созвездие, код Грея, аддитивный белый гауссовский шум, когерентный прием, отношение сигнал-шум, символьная вероятность ошибки, битовая вероятность ошибки.

CALCULATING METHOD ANALYSIS OF BIT PROBABILITY OF ERROR AT COGERENT RECEPTION OF SIGNALS WITH M-ARY PHASE MANIPULATION

Research article

Zubarev A.E.^1, *, Pozov A.V.², Prikhodko A.I.³

¹ ORCID: 0000-0003-0615-3414;

² ORCID: 0000-0001-6377-0756;

³ ORCID: 0000-0003-0108-8238;

^{1, 2, 3}Kuban State University, Krasnodar, Russia

* Corresponding author (shorshett1708919 [at] yandex.ru)

Abstract

In modern and promising digital telecommunication systems, signals with M-ary phase shift keying are widely used. The article discusses various methods for calculating the bit error probability for coherent reception of signals with M-ary phase shift keying in the communication channel with constant parameters and additive white Gaussian noise. The calculations of the bit error probability are carried out using exact and approximate formulas. Recommendations on the choice of approximate formulas for estimating the bit probability of error are justified.

Keywords: M-ary phase shift keying, signal constellation, Gray code, additive white Gaussian noise, coherent reception, signal-to-noise ratio, symbolic error probability, bit error probability.

В настоящее время в цифровых телекоммуникационных системах широкое применение получили сигналы с M-ичной (многократной) фазовой манипуляцией (МФМ) в силу своей достаточно высокой энергетической и спектральной эффективности [1, С. 87], [2, С. 243], [8, С. 228], [9, С. 206], [10, С. 148].

Сигнал с МФМ определяется выражением [2, С. 243], [10, С.150]

   (1) где A  – амплитуда сигнала;    (2) – прямоугольный видеоимпульс с единичной амплитудой и длительностью T; a_K – передаваемые M-ичные символы, каждый из которых при        (3) переносит    (4) бит информации и может принимать значения    (5) φ_d– девиация фазы, равная половине разности фаз Δφ    (6)

величина которой выбирается таким образом, чтобы векторы сигнального созвездия были расположены симметрично относительно начала координат, и составляет

     (7) – начальная фаза несущего колебания. Символы передаются с одинаковыми вероятностями     (8) и каждому из них однозначно соответствует кодовый блок, содержащий m двоичных символов (битов)    (9)

При описании сигналов с МФМ обычно рассматривают векторные диаграммы сигналов (сигнальные созвездия), которые представляют собой совокупность сигнальных векторов в декартовой системе координат с горизонтальной осью, соответствующей синфазной составляющей сигнала и вертикальной осью, отвечающей его квадратурной составляющей.

Сигнальные созвездия восьмифазного сигнала с МФМ при использовании натурального двоичного кода или кода Грея [1, С. 191] [3, С. 219], [10, С. 150] для кодирования двоичных информационных последовательностей (9) представлены на рис. 1.

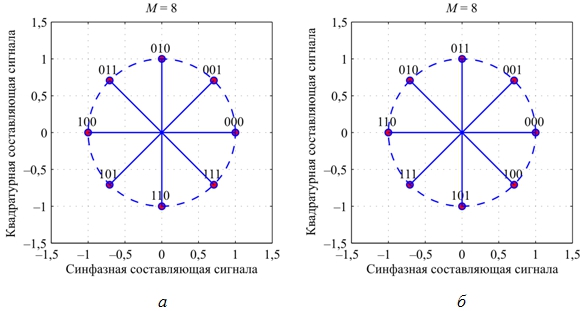
Рис. 1 – Сигнальные созвездия сигнала с МФМ: a – натуральный двоичный код; б – код Грея

 

Видим, что в отличие от натурального кода при использовании кода Грея двоичные последовательности (9), соответствующие соседним векторам сигнального созвездия, отличаются друг от друга лишь в одном разряде или, что то же самое, расстояние Хэмминга

между двумя соседними последовательностями  равно единице. Поскольку наиболее вероятной ошибкой при приеме сигнала с МФМ (символьной ошибкой) является регистрация сигнала, соответствующего одному из соседних сигнальных векторов, то наиболее вероятной будет ошибка лишь в одном разряде соответствующей комбинации двоичных символов (битовая ошибка). Поэтому при формировании сигналов с МФМ всегда используется код Грея [1, С. 191], [2, С. 244], [10, С. 150].

При оценке помехоустойчивости когерентного приема сигналов с МФМ (1)–(9) в канале с постоянными параметрами и аддитивным белым гауссовским шумом (АБГШ) получен ряд формул для расчета битовой вероятности ошибки.

Цель работы: провести сравнительный анализ различных методов расчета битовой вероятности ошибки при когерентном приеме сигналов с МФМ и определить условия применимости приближенных формул.

Точная формула для битовой вероятности ошибки, впервые полученная в [6, С. 490] и уточненная в [5, С. 1758], имеет вид

   (11)

где     (12)

– так называемое среднее спектральное расстояние [5, С. 1758], представляющее собой среднее расстояние Хэмминга между переданной двоичной последовательностью  и остальными последовательностями, отстоящими от нее на k шагов вдоль окружности сигнального созвездия;

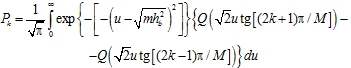   (13)

– вероятность того, что при передаче последовательности  (символа ) принимаемый сигнальный вектор попадет в k-ю область решения, представляющую собой сектор шириной  радиан, центрируемый вокруг каждой из сигнальных точек окружности сигнального созвездия;

   (14)

– Q-функция Гаусса [1, С. 52] [2, С. 234], [8, С. 147], [10, С. 950];    (15)

– отношение энергии двоичного элемента сигнала  на входе демодулятора к односторонней спектральной плотности мощности (интенсивности) АБГШ . Величина  представляет собой отношение сигнал-шум, приходящееся на один бит информации. В силу того, что длительность M‑ичного символа T в  раз больше длительности бита , энергия символа или элемента сигнала на входе модулятора составляет . Это означает, что величина (15) связана с отношением сигнал-шум на символ

  (16)

простым соотношением [1, С. 76], [2, С. 278], [8, С. 197]

   (17)

которое учтено в формуле (13).

Как указано в [6, С.489], [8, С. 232], при таком разбиения на области решения вероятность символьной ошибки составляет

    (18)

а вероятность правильного приема символа равна     (19) в силу того что сумма вероятностей (13) при k = 0, 1, 2, …, M равна единице:    (20)

Формула не удобна для расчетов и поэтому в [5, С. 1759] с использованием того, что код Грея относится к классу рефлексных кодов [3, С. 220], получено замкнутое выражение для вычисления среднего расстояния :

   (21)

где  – ближайшее целое к величине x.

При определении вероятностей P_k по формуле (13) необходимо вычислять интеграл с бесконечными пределами и подынтегральным выражением, содержащем Q-функцию Гаусса (14). Поэтому в [8, С. 233] на основе альтернативного представления Q-функции

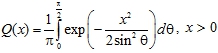   (22)

получена эквивалентная формула, включающая интегралы от элементарных функций с конечными пределами интегрирования:

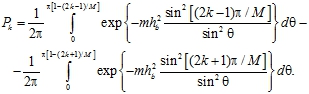   (23)

В [8, С. 233] также приведены развернутые выражения для битовой вероятности ошибки (11), получающиеся из формулы (21) при небольших значениях M:

     (24)      (25)     (26) При M = 4 формулы (23), (24) с использованием представления (22) сводятся к простому выражению      (27)

которое также определяет вероятность ошибки при когерентном приеме сигналов с двоичной фазовой манипуляцией [1, С. 53], [2, С. 279], [8, С. 228], [10, С. 139].

В силу того, что точные формулы (11), (21), (23) достаточно сложны, на практике часто используют различные приближенные методы оценки битовой вероятности ошибки.

Наиболее широкое применение среди таких методов получил метод, состоящий в предварительном вычислении символьной вероятности ошибки  и последующем расчете битовой вероятности ошибки  по простой приближенной формуле [1, С. 91], [2, С. 278], [9, С. 210], [10, С. 157]

    (28)

где учтено равенство (4). Выражение (28) также вытекает из равенств (11) и (18). Действительно, поскольку (11) в величина , справедливо неравенство

из которого с учетом (18) следует выражение (28).

При использовании приближенного равенства для расчета символьной вероятности ошибки, как правило, используют наиболее простую приближенную формулу [1, С. 90], [2, С. 281]

   (29)

которая при подстановке (29) в (28) дает следующее выражение:

    (30)

Вместо приближенной формулы (29) в (28) также можно использовать точную формулу для символьной вероятности ошибки [2, С. 289], [8, 230]

   (31)

полученную в [4, С. 25.5.2] на основе альтернативного представления (22) Q-функции Гаусса (14). В этом случае подстановка  (31) в (28) дает следующее приближенное выражение для битовой вероятности ошибки:

   (32)

Наконец, в [8, С. 234], [10, С. 158] приведена еще одна приближенная формула, предложенная в [7, С. 183] с использованием простого геометрического подхода, основанного на понятиях сигнального пространства:

    (33)

При учете только первого слагаемого формула (33) составляет

и совпадает с выражением (30).

В [7, С. 184] с использованием метода статистического моделирования (метода Монте-Карло) была проведена проверка точности формулы (33) при 0 дБ ≤ ≤ 10 дБ и M = 16, 32. На основании полученных результатов было указано, что при   в формуле (33) следует учитывать только первое и второе слагаемые, когда она принимает вид

Результаты расчетов зависимостей битовой вероятности ошибки  от отношения сигнал-шум  по точным формулам (11), (21), (23) и по приближенным формулам (30), (32), (33), (34) при M = 8, 16 и M = 32, 64 представлены на рис. 2 и рис. 3 соответственно.

Из графиков следует:

– формулы (30), (32) дают нижнюю границу вероятности ошибки, а формула (33) – верхнюю;

– формула (34) при M = 8 дает верхнюю границу, при M = 16 практически точные результаты, а при  – нижнюю границу вероятности ошибки;

– формула (30) при малых значениях M дает лучшие результаты, чем более сложная формула (32).

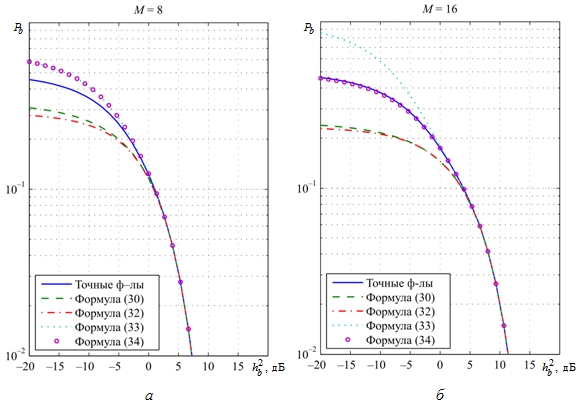
Рис. 2 – Зависимости вероятности ошибки

от отношения сигнал-шум при различных значениях M: a – M = 8; б – M = 16

 

Таким образом, проведенные расчеты позволяют сделать вывод о том, что наибольшее предпочтение следует отдать простым приближенным формулам (30) или (34):

– формула (30) дает точные результаты при M = 8 и  ≥ 0 дБ, при M = 16 и 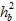 ≥ 4 дБ, при M = 32 и  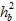≥ 8 дБ, при M = 64 и  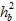≥ 13 дБ;

– формула (34) дает точные результаты при M = 16 и любых значениях 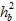, при M = 8, M = 32 и  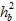≥ 0 дБ, при M = 64 и  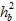≥ 4 дБ.

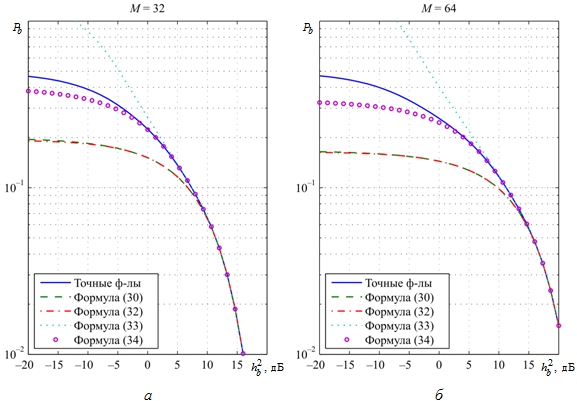
Рис. 3 – Зависимости вероятности ошибки

от отношения сигнал-шум при различных значениях M: a – M = 32; б – M = 64

Конфликт интересов Не указан.

Conflict of Interest None declared.

Список литературы / References

1. Варгаузин В.А. Методы повышения энергетической и спектральной эффективности цифровой радиосвязи / В.А. Варгаузин, И.А.Цикин. – СПб.: БХВ-Петербург, 2013. – 352с.
2. Голдсмит А. Беспроводные коммуникации / А. Голдсмит. – М.: Техносфера, 2011. – 904с.
3. Приходько А.И. Детерминированные сигналы / А.И. Приходько. – М.: Горячая линия–Телеком, 2013. – 326с.
4. Craig J. New, simple and exact result for calculating the probability of error for two-dimensional signal constellations / J.Craig // Proc. Military Commun. Conf. 1991. November. P. 25.5.1–25.5.5.
5. Lassing J. Computation of Exact Bit-Error Rate of Coherent M-ary PSK With Gray Code Bit Mapping / J. Lassing, E.G. Ström, E. Angrell and others // IEEE Trans. Commun. 2003. Vol. 51. № 11. P. 1758–1760.
6. Lee P.J. Computation of the Bit Error Rate of Coherent M-ary PSK with Gray Code Bit Mapping / P.J. Lee // IEEE Trans. Commun. 1986. Vol. 34. № 5. P. 488–491.
7. Lu J. M-PSK and M-QAM BER Computation Using Signal-Space Concepts / J. Lu, K.B. Letaief, J. C-I. Chuang and others // IEEE Trans. Commun. 1999. Vol. 47. № 2. P. 181–184.
8. Simon M.K. Digital Communication over Fading Channels / M.K. Simon, M.-S.Alouini. – Hoboken: Wiley, 2004. – 900 p.
9. Simon M.K. Digital Communication Techniques: Signal Design and Detection / M.K. Simon, S.M.Hinedi, W.C.Lindsey. – Englewood Cliffs: Prentice Hall, 1994. – 888 p.
10. Xiong F. Digital Modulation Techniques / F. Xiong. – Boston – London: Artech House, 2006. – 1017 p.

Список литературы на английском языке / References in English

1. Vargauzin V.A. Metody povyshenija jenergeticheskoj i spektral'noj jeffektivnosti cifrovoj radiosvjazi [Methods to improve the energy and spectral efficiency of digital radio] / V.A. Vargauzin, I.A.Cikin. – SPb.: BHV-Peterburg, 2013. – 352 p. [in Russian]
2. Goldsmit A. Besprovodnye kommunikacii [Wireless Communications] / A. Goldsmit. – M.: Tehnosfera, 2011. – 904 p. [in Russian]
3. Prihod'ko A.I. Determinirovannye signaly [Deterministic Signals] / A.I. Prihod'ko. – M.: Gorjachaja linija–Telekom, 2013. – 326 p. [in Russian]
4. Craig J. New, simple and exact result for calculating the probability of error for two-dimensional signal constellations / J.Craig // Proc. Military Commun. Conf. 1991. November. P. 25.5.1–25.5.5.
5. Lassing J. Computation of Exact Bit-Error Rate of Coherent M-ary PSK With Gray Code Bit Mapping / J. Lassing, E.G. Ström, E. Angrell and others // IEEE Trans. Commun. 2003. Vol. 51. № 11. P. 1758–1760.
6. Lee P.J. Computation of the Bit Error Rate of Coherent M-ary PSK with Gray Code Bit Mapping / P.J. Lee // IEEE Trans. Commun. 1986. Vol. 34. № 5. P. 488–491.
7. Lu J. M-PSK and M-QAM BER Computation Using Signal-Space Concepts / J. Lu, K.B. Letaief, J. C-I. Chuang and others // IEEE Trans. Commun. 1999. Vol. 47. № 2. P. 181–184.
8. Simon M.K. Digital Communication over Fading Channels / M.K. Simon, M.-S.Alouini. – Hoboken: Wiley, 2004. – 900 p.
9. Simon M.K. Digital Communication Techniques: Signal Design and Detection / M.K. Simon, S.M.Hinedi, W.C.Lindsey. – Englewood Cliffs: Prentice Hall, 1994. – 888 p.
10. Xiong F. Digital Modulation Techniques / F. Xiong. – Boston – London: Artech House, 2006. – 1017 p.