ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РАСЧЕТНОГО СОПРОТИВЛЕНИЯ И ФОРМЫ СЕЧЕНИЯ ДВУТАВРОВОЙ БАЛКИ
Лиманцев А.А.1, Денисенко А.В.2
1,2Донской государственный технический университет, Академия строительства и архитектуры
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО РАСЧЕТНОГО СОПРОТИВЛЕНИЯ И ФОРМЫ СЕЧЕНИЯ ДВУТАВРОВОЙ БАЛКИ
Аннотация
Приведено решение задачи о определении оптимального расчетного сопротивления для стальной двутавровой балки из соображений проектирования наименее металлоемкого сечения. Дано определение и формулы для определения удельных характеристик сечения Показаны наилучшие распределения материала в сечении при использовании сталей с разными сопротивлениями. В случае, если определяющим является условие прочности, оптимальное распределение материала по сечению a=0,5, если жесткость – a=0,75 Найдено эталонное сечение двутавровой балки для данных условий.
Ключевые слова: стальная балка, двутавр, высокопрочная сталь, расчетное сопротивление, жесткость.
Limantsev A.A.1, Denisenko А.V.2
1Don State Technical University, Academy of Civil Engineering and Architecture
2Don State Technical University, Academy of Civil Engineering and Architecture
DETERMINATION OF OPTIMAL DESIGN RESISTANCE AND SECTION SHAPE OF BILATERAL BEAM
Abstract
The solution of the problem on determining the optimal design resistance for a steel bilateral beam is proposed in virtue of design the least metal-intensive section. The definition and formulas for determining the specific characteristics of the section are given. The best material distribution in the cross section is shown when using steels with different resistances. In case if the strength condition is the determining factor, the optimal material distribution over the cross-section a=0.5, if the rigidity is a=0.75. I found the reference cross section of the bilateral beam for these conditions.
Keywords: steel beam, bilateral beam, high-strength steel, design resistance, rigidity.
В настоящее время одним из основных направлений развития проектирования металлических конструкций является применение сталей повышенной и высокой прочности. Применяя такие стали можно существенно сократить металлоемкость конструкций. Однако не во всех случаях увеличение расчетного сопротивления приводит к уменьшению поперечного сечения и в таком случае применение высокопрочной стали будет не целесообразно. В данной статье приводится решение задачи поиска оптимального расчетного сопротивления стали для двутавровой балки.
Для решения задачи наименее металлоемкого сечения удобно разделить эту задачу на две части: поиск формы и поиск размеров при заданной форме.
Таким образом мы уменьшаем количество вариантов. Первоначально выбираем оптимальную форму, а затем находим необходимую площадь поперечного сечения. Определение величины площади поперечного сечения при известной оптимальной форме, будет иметь единственное решение [2].
В геометрических характеристиках сечения удобно отделить форму от размеров сечения вводя понятие удельная характеристика сечения. В таком случае мы сможем составить следующие зависимости:
![]() (1)
(1)
![]() (2)
(2)
Удельные характеристики двутаврового сечения ω и ρ определяются по формулам (3) и (4) соответственно.
![]() (3)
(3)
![]() (4)
(4)
Оптимальная форма сечения при внецентренном сжатии стержня будет при которой нормальные напряжения в сечении будут минимальными. Тогда оптимальной форме внецентренно-сжатого стержня соответствует сечение с ![]() . Оптимальная форма при изгибе по условию прочности получается в случае
. Оптимальная форма при изгибе по условию прочности получается в случае ![]() . По условию жесткости для изгибаемого стержня оптимальной будет форма сечения, которой соответствует наименьший прогиб. Тогда следует, что оптимальную форму получим когда
. По условию жесткости для изгибаемого стержня оптимальной будет форма сечения, которой соответствует наименьший прогиб. Тогда следует, что оптимальную форму получим когда ![]() .
.
С помощью выражения (1) можно определить площадь сечения изгибаемого элемента двутаврового сечения, рассчитываемого по прочности [5]. Площадь сечения, рассчитываемого на жесткость, находится по (2).
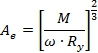 (5)
(5)
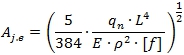 (6)
(6)
Принимая во внимание формулу (1) можно составить выражение для определения коэффициента изменения массы изгибаемого элемента, рассчитываемого по прочности без учета изменения гибкости стенки (5) и с учетом изменения (6). Так же используя формулу (2), получим коэффициент массы при расчете на жесткость с учетом изменения гибкости стенки (7). Если изменение гибкости стенки не учитывать, то ![]() . Для сравнения вариантов, отличающихся расчетным сопротивлением, составим формулы для определения площади сечения при расчете на: прочность – (10), жесткость – (11). Оптимальное расчетное сопротивление Ry получим из условия (12).
. Для сравнения вариантов, отличающихся расчетным сопротивлением, составим формулы для определения площади сечения при расчете на: прочность – (10), жесткость – (11). Оптимальное расчетное сопротивление Ry получим из условия (12).
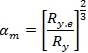 (7)
(7)
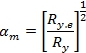 (8)
(8)
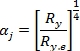 (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Выражение для определения оптимального расчетного сопротивления в аналитическом виде может быть получено для геометрически подобных сечений в виде (13), где коэффициент ![]() . Для сечений с учетом влияния местной устойчивости в виде (14), где коэффициент
. Для сечений с учетом влияния местной устойчивости в виде (14), где коэффициент ![]() .
.
![]() (13)
(13)
![]() (14)
(14)
Решим задачу определения оптимального расчетного сопротивления по условиям прочности и жесткости для рядовой балки балочной клетки. В качестве примера взята второстепенная балка рабочей площадки комплекса доменной печи №7 ПАО «НЛМК» со следующими исходными данными: пролет l=6м, расчетный момент M=0.302 МН∙м, момент от нормативной нагрузки Mн=0.259 МН∙м. Гибкость стенки λω принимаем равным 100. Максимальный допустимый прогиб, согласно , [f/l]=1200.
Удельные характеристики по формулам (3) и (4) будут равны соответственно:
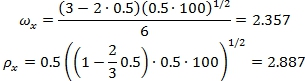
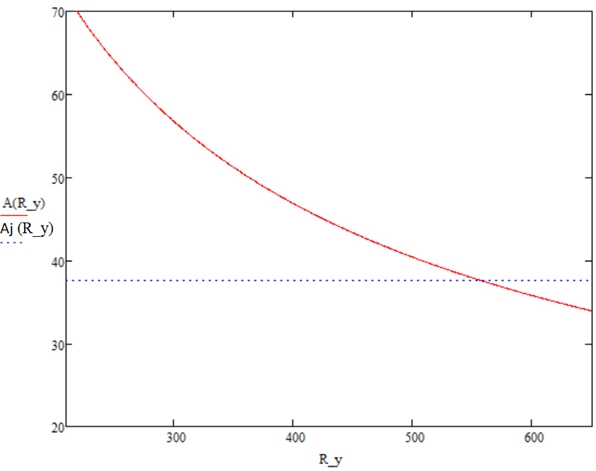
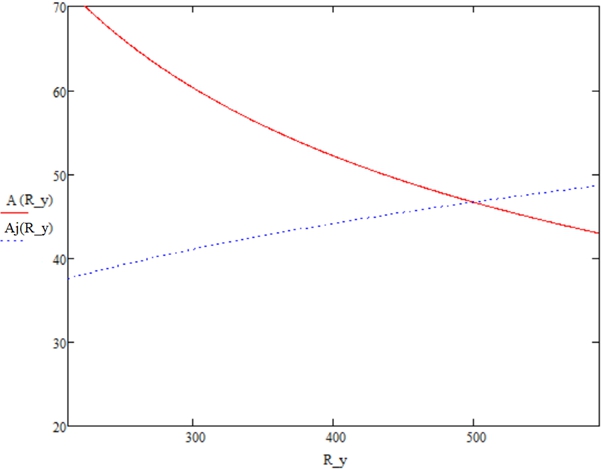
Графические решения представлены на рис. 1, 2. Эталонные сечения для сравнения имеют ![]() ,
, ![]() ,
, ![]() . Оптимальное решение получено в случае сохранения геометрического подобия при
. Оптимальное решение получено в случае сохранения геометрического подобия при ![]() , в случае учета изменения гибкости стенки
, в случае учета изменения гибкости стенки ![]() .
.
Рис. 1 – Изменение площади поперечного сечения без учета изменения гибкости стенки в зависимости от расчетного сопротивления
Рис. 2 – Изменение площади поперечного сечения с учетом изменения гибкости стенки в зависимости от расчетного сопротивления
Из этого следует, что в данных балках, из соображений проектирования наименее металлоемкого сечения, целесообразно применять стали высокой прочности. При применении стали С440 площадь сечения ![]() , при С590 –
, при С590 –![]() .
.
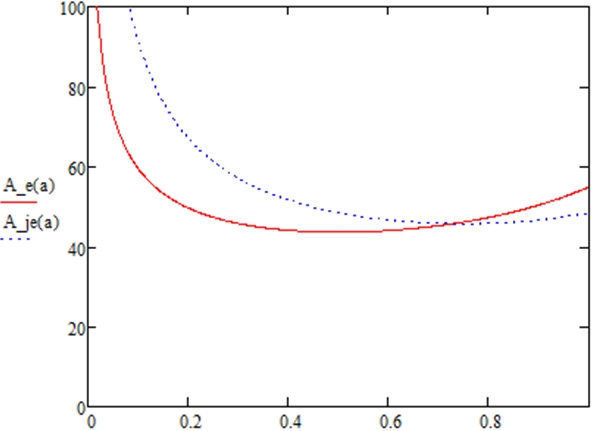
Теперь определим коэффициенты распределения материала в сечении симметричного двутавра, обеспечивающие минимальное значение площади по условиям прочности и жесткости. Варьируя коэффициентом распределения материала по сечению а в пределах 0,1-1,0 по формулам (5) и (6) найдем площади сечений [3]. Решение представлено в виде графика на рисунке 3,. при ![]() ,
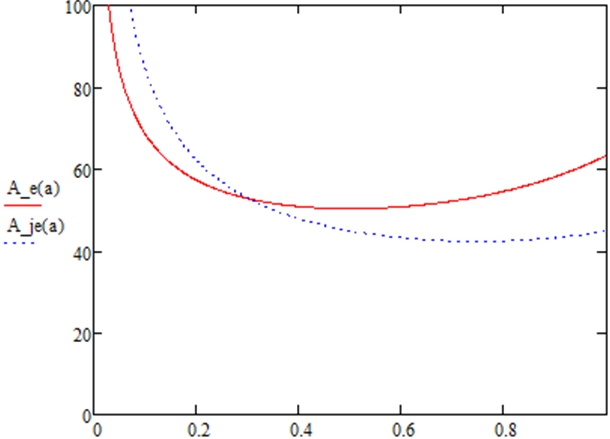
, ![]() , [l/f]. Оптимальный коэффициент в данных условиях a=0.72. На рисунке 4 решение для стали с расчетным сопротивлением
, [l/f]. Оптимальный коэффициент в данных условиях a=0.72. На рисунке 4 решение для стали с расчетным сопротивлением ![]() и
и ![]() . В этом случае нужно принимать a=0.5.
. В этом случае нужно принимать a=0.5.
Рис. 3 – Изменение площади поперечного сечения в зависимости от коэффициента распределения материала по сечению для стали С590
Рис. 4 – Изменение площади поперечного сечения в зависимости от коэффициента распределения материала по сечению для стали С440
В случае, если при расчете балки в упругой стадии определяющим является условие прочности, оптимальная форма балки – двутавр симметричный с a=0.5, ![]() . Если определяющим является условие жесткости, то оптимальная форма имеет место при a=0.75,
. Если определяющим является условие жесткости, то оптимальная форма имеет место при a=0.75, ![]() . В случае, когда определяющими могут быть и условие прочности, и условие жесткости, оптимальная форма определяется коэффициентом a=0.5÷0.75.
. В случае, когда определяющими могут быть и условие прочности, и условие жесткости, оптимальная форма определяется коэффициентом a=0.5÷0.75.
Зная оптимальные значения расчетного сопротивления и коэффициента распределения материала, решим задачу определения эталонного двутаврового сечения [4]. При ![]() ,
, ![]() ,
, ![]() , a=0.5. Удельные характеристики
, a=0.5. Удельные характеристики ![]() .
.
Определяем площадь сечения из условия прочности ![]()
Определяем площадь сечения из условия жесткости ![]()
Площадь стенки ![]()
Площадь полки ![]()
Высота стенки ![]()
Толщина стенки ![]()
Ширина полки ![]()
Толщина полки ![]()
Таким образом, решив эти задачи, мы можем запроектировать двутавровую балку с наименьшей площадью поперечного сечения и, следовательно, наименьшим расходом стали.
Список литературы / References
- СП 16.13330.2011. Стальные конструкции. Актуализированная редакция СНиП II-23-81*. – Введ. 2011–05–20. – М. : Минрегион России, 2010. – 173 с.
- СП 20.13330.2011. Нагрузки и воздействия. Актуализированная редакция СНиП 2.01.07-85*. – Введ. 2011–05–20. – М. : Минрегион России, 2010. – 80 с.
- Стрелецкий Н.С. Проектирование и изготовление экономичных металлических конструкций: Материалы к курсу металлических конструкций // Н.С. Стрелецкий, Д.Н. Стрелецкий. – Вып. IV. – М. : Строиздат, 1964.– 360 с.
- Стрелецкий Н.С. Основы законов веса металла в промышленных конструкциях: Сборник статей по металлическим конструкциям // Н.С. Стрелецкий. – М. : Стройиздат, 1934. – С. 3-37.
- Шумицкий О.И. О рациональных конструктивных формах сварных МК: Металлические конструкции: Работы школы проф. Н.С. Стрелецкого // О.И. Шумицкий – М. : Стройиздат, 1966. – С. 420-429.
- Сергеев Н.Д. Проблемы оптимального проектирования конструкций // Н.Д. Сергеев, А.И. Богатырев. – Л. : Стройиздат, 1971.– 136 с.
- Шефтель Н.И. Улучшение качества и сортамента проката // Н.И. Шефтель. – М. : Металлургия, 1973.– 343 с
- Шварцбург Б.Г. Весовые показатели металлических перекрытий // Б.Г. Шварцбург, ЯЛ. Куценок. – Харьков : ОНТИ НКТП, 1934.– 44 с.
- Чернашкин В.Г. Особенности изготовления конструкций из сталей высокой прочности: Монтажные работы в строительстве // В.Г. Чернашкин, В.С. Москвитин, У.ГГ. Шибаев. – ЦБТН, 1967. Вып. 2
- Указания по эффективному применению низколегированных сталей в строительных МК: СН 316-65. – М.: Стройиздат, 1966.– 11 с.
Список литературы на английском языке / References in English
- SP 16.13330.2011. Stal'nyye konstruktsii. Aktualizirovannaya redaktsiya SNiP II-23-81* [Steel Structures. Updated Version of SNiP II-23-81*]. - Intr. 2011-05-20. - M.: Ministry of Regional Development of Russia, 2010. - 173 p. [In Russian]
- SP 20.13330.2011. Nagruzki i vozdeystviya. Aktualizirovannaya redaktsiya SNiP 2.01.07-85* [Loads and Impacts. Updated Version of SNiP 2.01.07-85*]. - Intr. 2011-05-20. - M.: Ministry of Regional Development of Russia, 2010. - 80 p. [In Russian]
- Streletsky N.S. Proyektirovaniye i izgotovleniye ekonomichnykh metallicheskikh konstruktsiy: Materialy k kursu metallicheskikh konstruktsiy [Designing and Manufacturing Economical Metal Structures: Materials to Course of Metal Constructions] // N.S. Streletsky, D.N. Streletsky. - Is. IV. - M.: Stroizdat, 1964. - 360 p. [In Russian]
- Streletsky N.S. Osnovy zakonov vesa metalla v promyshlennykh konstruktsiyakh: Sbornik statey po metallicheskim konstruktsiyam [Fundamentals of Laws of Weight of Metal in Industrial Designs: Collection of Articles on Metal Structures] // N.S. Streletsky. - M.: Stroyizdat, 1934. - P. 3-37. [In Russian]
- Shumitsky O.I. O ratsional'nykh konstruktivnykh formakh svarnykh MK: Metallicheskiye konstruktsii: Raboty shkoly prof. N.S. Streletskogo [On Rational Constructive Forms of Welded MS: Metal structures: Works of School of Prof. N.S. Streletsky] // O.I. Shumitsky - M.: Stroyizdat, 1966. - P. 420-429. [In Russian]
- Sergeev N.D. Problemy optimal'nogo proyektirovaniya konstruktsiy [Problems of Optimal Design of Structures] // N.D. Sergeev, A.I. Bogatyrev. - L.: Stroyizdat, 1971.- 136 pp. [In Russian]
- Sheftel N.I. Uluchsheniye kachestva i sortamenta prokata [Improvement of Quality and Assortment of Rolled Steel] // N.I. Sheftel. - M.: Metallurgy, 1973.- 343 p. [In Russian]
- Schwarzburg B.G. Vesovyye pokazateli metallicheskikh perekrytiy [Weighted Indices of Metal Overlaps] // B.G. Schwarzburg, Ya.L. Kutsenok. - Kharkov: ONTI NKTP, 1934.- 44 p. [In Russian]
- Chernashkin V.G. Osobennosti izgotovleniya konstruktsiy iz staley vysokoy prochnosti: Montazhnyye raboty v stroitel'stve [Features of Manufacture of Structures of High-strength Steel: Installation Work in Construction] // V.G. Chernashkin, V.S. Moskvitin, U.G. Shibaev. - CBTN, 1967. Issue. 2 [In Russian]
- Ukazaniya po effektivnomu primeneniyu nizkolegirovannykh staley v stroitel'nykh MK: SN 316-65 [Instructions on the effective use of low-alloy steels in building materials: CH 316-65.] - Moscow: Stroiizdat, 1966. - 11 p. [In Russian]