МАТЕМАТИЧЕСКАЯ ФОРМАЛИЗАЦИЯ ПРЕОБРАЗОВАНИЙ ПРИ ПЕРЕДАЧЕ ПО КАНАЛАМ ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ

Кузнецов А.Г.

Кандидат технических наук,

Пермский государственный национальный исследовательский университет

МАТЕМАТИЧЕСКАЯ ФОРМАЛИЗАЦИЯ ПРЕОБРАЗОВАНИЙ ПРИ ПЕРЕДАЧЕ ПО КАНАЛАМ ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ ГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ

Аннотация

Описана одна из задач представления графической информации в интеллектуальных телекоммуникационных системах, в первую очередь – изображений. Предложена схема восходящего анализа, в которой последовательность групп преобразований упорядочивается отношением «группа – надгруппа». Кратко описаны достоинства этой схемы. Приведено описание преобразований графических изображений при передаче по каналам телекоммуникационных связей. Описана математическая формализация этих преобразований, включающая в себя тождественные преобразования,  трансляции, центроафинные ротации,  центроафинно-аксиальные бикомпресии, движения и нерефлексные аффинные преобразования. Сформулированы свойства структурных элементов для различных основных групп преобразований. Отмечено, что математически формализованный анализ преобразований дает возможность осуществлять структурное описание графических изображений с их геометрико-топологическими свойствами, характеристиками и взаимосвязями, что важно, например, при организации передачи графических изображений по каналам телекоммуникационных систем и при сжатии изображений в процессе этой передачи.

Ключевые слова: телекоммуникации, изображения, графическая информация, преобразования графических изображений, математическая формализация, группы преобразований.

Kuznetsov A.G.

PhD in Engineering

Perm State National Research University

MATHEMATICAL FORMALIZATION OF TRANSFORMATIONS IN TRANSMISSION VIA CHANNELS OF TELECOMMUNICATION SYSTEMS OF GRAPHIC IMAGES

Abstract

The paper considres one of the problems of representation of graphical information in intelligent telecommunication systems, images first of all. An outline analysis scheme is proposed, in which the sequence of transformation groups is ordered by the group-over-group relationship. The advantages of this scheme are briefly described. The description of transformations of graphic images is given at transmittion via telecommunication channels. A mathematical formalization of these transformations is described, including identical transformations, translations, centrifugal rotations, central-affine-axial bicompressions, motions, and non-reflex affine transformations. The properties of structural elements for various basic transformation groups are formulated. It is noted that mathematically formalized analysis of transformations makes it possible to carry out a structural description of graphic images with their geometric-topological properties, characteristics and interrelations, which is important, for example, when organizing the transmittion of graphic images through the channels of telecommunication systems and when compressing images during this transmittion.

Keywords: telecommunications, images, graphic information, graphic image transformation, mathematical formalization, transformation groups.

Проблема передачи больших объемов информации по каналам связи телекоммуникационных систем продолжает сохранять свою актуальность. Это, во многом, обусловлено, как увеличением количества абонентов телекоммуникационных систем, так и широким, постоянно возрастающим использованием современных информационных технологий абонентами. Поэтому важны разработки, связанные с созданием способов и методов моделирования, представления и кодирования структуры графических изображений. Особенно актуальны методы представления и преобразования графических изображений, основанные на новых эффективных моделях их описания и порождающие алгоритмы, программы и технологии обработки таких изображений. Важно также решение задач практической реализации алгоритмов при передаче графической информации по каналам связи телекоммуникационных систем и использовании эффективных алгоритмов в системах обработки графической информации.

Решение проблемы передачи больших объемов информации по каналам связи в значительной мере осложняется тем, что передаваемая информация имеет сложную структуру и разнообразные формы организации [1, С. 5]. Одной из наиболее актуальных на сегодняшний день представлений сложной информации в интеллектуальных телекоммуникационных системах является задача представления графической информации, в первую очередь – изображений, ввиду их разнообразия, сложности структуры и большой информационной емкости. В настоящее время создан метод формирования описаний пространственной структуры (ПС) графических изображений (ГИ), основанный на анализе преобразований графических изображений, описываемых их группами [2, С. 64]. При создании этого метода используется свойство трансформационной устойчивости ПС – инвариантность структурных элементов (СЭ), их характеристик и взаимосвязей при воздействии на структуры различных видов преобразований пространственного характера, индуцируемых группами преобразований пространства [3, C. 175]. Поэтому суть метода  анализа преобразований заключается в определении инвариантов структуры относительно различных групп преобразований. При этом рассматривается последовательность групп преобразований, упорядоченная отношением «группа – подгруппа» [4, С. 198].

Но интересен иной подход – схема восходящего анализа, в которой последовательность групп преобразований упорядочивается отношением «группа – надгруппа» [5, С. 41]. В этой схеме происходит обратный процесс сборки СЭ из отдельных точек ГИ, и ПС воссоздается путем установления взаимосвязей элементов. Формируемая модель ПС в этом случае имеет более простой и менее избыточный вид по сравнению с моделью, получаемой при нисходящей схеме анализа [6, С. 80]. В то же время остается возможной ее достройка до уровня избыточности модели нисходящей схемы [7, С. 82], имеющей важное значение для решения задач интерпретации ПС ГИ. Для решения этой задачи важно формализованное описание преобразований. Эта формализация, например, может существенно упростить запись алгоритмов, например, приведенных в работе [8, С. 635]. Математическая формализация всех возможных преобразований приведена ниже.

Если задана группа преобразований пространства (в данном случае, пространства размерности 2 – плоскости) G, то тем самым для точек изображения определено отношение G-эквивалентности: две точки изображения G - эквивалентны, если существуют  , взаимно преобразующие их вместе с окрестностями:

здесь Sg(x, y) ∩ B(x,y) обозначает сужение функции (сигнатурно-кодовой карты) Sg(x, y) на окрестность точки  B(x,y) [3, С .65] .

Очевидно, что необходимым (но не достаточным) условием G-эквивалентных точек    является равенство их кодовых сигнатур:

 

Для проведения анализа преобразований введем в рассмотрение последовательность основных преобразований, сформированных из образующих групп (см. табл. 1).

Таблица 1 – Трансформации графических изображений

Используются три образующих группы преобразований:

– группа трансляций  – сдвигов, параллельных осям координат;

– группа центроафинных ротаций  – поворотов вокруг начала координат;

– группа центроафинно-аксиальных биокомпрессий  – сжатий-растяжений относительно начала координат в направлениях осей координат.

Три основных группы преобразований являются прямыми произведениями перечисленных выше трех подгрупп и образуются суперпозициями соответствующих преобразований:

– группа трансляций  – совпадает с первой образующей группой;

– группа движений  (нецентрированных ротаций) – суперпозиций поворотов и сдвигов; является прямым произведением групп ротаций и трансляций ;

– группа нерефлексных аффинных преобразований  – суперпозиций поворотов, бикомпрессий и сдвигов; является прямым произведением групп ротаций, биокомпрессий и трансляций .

Очевидно, что группа трансляций является подгруппой группы движений, а группа движений – подгруппой нерефлексных аффинных преобразований:

Все основные группы являются подгруппами группы аффинных преобразований и, следовательно, наследуют все ее инварианты, а группа аффинных преобразований является подгруппой группы всех непрерывных преобразований и наследует ее инварианты. Поэтому для всех основных групп преобразований инвариантной будет такая характеристика многообразий, как их размерность, такое ее свойство, как связность, и такое отношение, как смежность.

На рис.1 – 7  приведены иллюстрация видов возможных трансформаций, математическая формализация которых описана в настоящей статье.

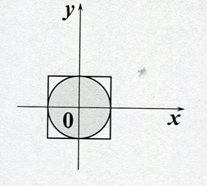
Рис. 1 – Тождественные преобразования Id

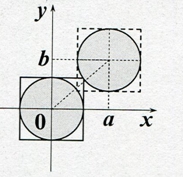
Рис. 2 – Трансляции Tr[a,b]

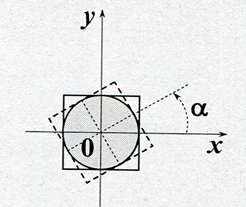
Рис. 3 – Центроаффинные ротации Rt[a]

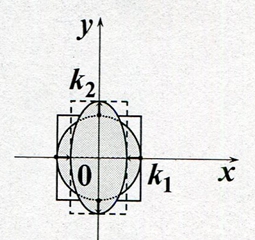
Рис. 4 – Центроаффинно-аксиальные бикомпресии 

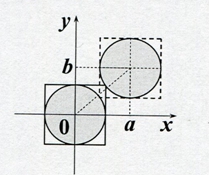
Рис. 5 – Трансляции Tr[a,b]

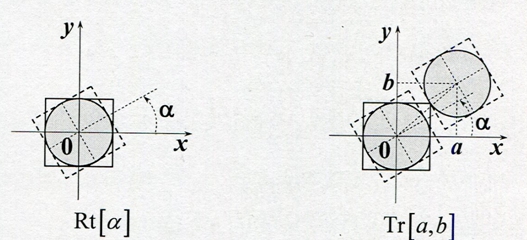
Рис. 6 – Движения 

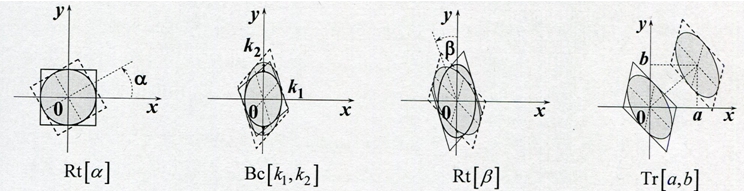
Рис. 7 – Нерефлексные аффинные преобразования 

При анализе ПС ГИ можно использовать следующие свойства СЭ относительно G-эквивалентности для различных основных групп преобразований.

Свойство 1. Все внутренние точки планарного СЭ  -эквивалентны, а также -эквивалентны и -эквивалентны.

Свойство 2. Все внутренние точки прямолинейного линейного СЭ -эквивалентны, а также -эквивалентны и -эквивалентны.

Свойство 3. Все внутренние точки дугообразного линейного СЭ -эквивалентны и -эквивалентны.

Свойство 4. Все внутренние точки линейного СЭ -эквивалентны и -эквивалентны.

Отметим, что свойства 1–3 представляются достаточно очевидными, т.к. G-эквивалентность точек устанавливается путем сдвига одной из точек вместе с ее окрестностью до совмещений ее с другой точкой (свойства 1–2 ), либо путем сдвига одной из точек вместе с ее окрестностью до совмещения ее с другой точкой и поворота ее окрестности до совмещения касательных к дугам в окрестностях обеих точек (свойство 3).

Таким образом, предложенный в статье математически формализованный анализ преобразований дает возможность осуществлять структурное описание ПС ГИ с их геометрико-топологическими свойствами, характеристиками и взаимосвязями, что важно, например, при организации передачи графических изображений по каналам телекоммуникационных систем [ 9, С. 172] и при сжатии изображений [10, С. 7].

Список литературы / References

1. Кузнецов А.Г. Структурные представления и методы кодирования графических изображений в интеллектуальных телекоммуникационных системах: дисс. … канд. тех. наук : 05.12.13 : защищена 17.12.2008г. : утв. 19.06.2009г  ./ Кузнецов Андрей Геннадьевич. – Ижевск. ИжГТУ., 2008. – 164с.
2. Кузнецов А.Г. Использование преобразований для сжатия графической информации / А.Г. Кузнецов, А.Я. Уфимкин// Вестник Московской Академии рынка труда и информационных технологий. – 2004. - №4(12). – С.62 – 73.
3. Колмогоров А.Н. Элементы теории функций и функционального анализа/ А.Н.Колмогоров, С.В. Фомин. – М.: Наука. – 1981. – 544 с.
4. Мурынов А.И. Структурно-цветовой анализ графических изображений на основе динамической экстентной модели кластера/ А.И. Мурынов, М.В.Телегина //Известия Института математики и информатики Удмуртского государственного университета. – 2006. – №2. – С. 197-200.
5. Чернышев К.С. Анализ цифровых представлений и моделей трехмерных пространственных объектов/ К.С. Чернышев, А.И. Мурынов, А.Д. Борин//Приволжский научный вестник. – 2014. – №7 (35). – С. 39 – 42.
6. Пасичник С., Бахич В.,, Журавлев A. Передача данных: от каналов к пакетам/ Пасичник С., Бахич В.,, Журавлев A. // Сети и телекоммуникации. – 2006. -  № 1-2. – С.. 45 – 52.
7. Пивоваров И.В. Алгоритм структурно-цветового анализа графических изображений/ И.В. Пивоваров// Наукоемкие технологии и интеллектуальные системы 2005. – Сб. научн. тр. VII Молодежной НТК – Москва: Изд-во МГТУ им Н.Э. Баумана. – 2005. – С.79 – 83.
8. Kwok P. Customising thining algorithms/ P.Kwok // 3rt Int. Conf. Image Proc. and Appl., Warwik, 18 – 20 July. – 1989. – London. – 1989. – Pp.633 – 637.
9. Лурье И., Косиков А. Теория и практика цифровой обработки изображений / И.Лурье, А.Косиков. -  М.: Научный Мир. – 2003. – 176с.
10. Миано Д. Форматы и алгоритмы сжатия изображений в действии /Д. Миано. – М.: Триумф. – 2003. – 336 с.

Список литературы на английском языке / References in English

1. Kuznetsov A.G. Strukturnye predstavlenija i metody kodirovanija graficheskih izobrazhenij v intellektual'nyh telekommunikacionnyh sistemah [Structural representations and methods of encoding graphic images in intelligent telecommunication systems [Structural representations and methods of encoding graphic images in intelligent telecommunication systems] : dis. … of PhD in Engineering : 05.12.13 : defense of the thesis 17.12.08 : approved 19.06.09/ Kuznetsov Andrej Gennad'evich. – Izhevsk. Vuz., 2008. – 164 p. [in Russian]
2. Kuznetsov A.G. Ispol'zovanie preobrazovanij dlja szhatija graficheskoj informacii [Using transformations to compress graphic information] / A.G. Kuznetsov, A.Ja. Ufimkin// Vestnik Moskovskoj Akademii rynka truda i informacionnyh tehnologij [Bulletin of the Moscow Academy of Labor and Information Technology]. – 2004. - №4(12). – Pp.62 – 73. [in Russian]
3. Kolmogorov A.N. Jelementy teorii funkcij i funkcional'nogo analiza [Elements of the theory of functions and functional analysis]. – M.: Nauka. – 1981. – 544 p. [in Russian]
4. Murynov A.I, Telegina M.V. Strukturno-cvetovoj analiz graficheskih izobrazhenij na osnove dinamicheskoj jekstentnoj modeli klastera [Structural-color analysis of graphic images based on the dynamic extent of the cluster model ]// Izvestija Instituta matematiki i informatiki Udmurtskogo gosudarstvennogo universiteta[Proceedings of the Institute of Mathematics and Informatics of the Udmurt State University]. – 2006. – № 2. – Pp. 197-200. [in Russian]
5. Chernyshev K.S., Murynov A.I., Borin A.D. Analiz cifrovyh predstavlenij i modelej trehmernyh prostranstvennyh ob’ektov [Analysis of digital representations and models of three-dimensional objects ] //Privolzhskij nauchnyj vestnik [Privolzhsky Scientific Bulletin]. – 2014. – № 7 (35). – Pp. 39 – 42. [in Russian]
6. Pasichnik S.. Bakhich V., Zhuravlev A. Peredacha dannykh: ot kanalov k paketam [Data transfer: from channels to packets ] // Seti i telekommunikatsii [Networks and telecommunications]. – 2006. - № 1-2. – Pp. 45 – 52. [in Russian]
7. Pivovarov I.V. Algoritm strukturno-tsvetovogo analiza graficheskih izobrazheniy [Algorithm of structural-color analysis of graphic images] // Naukoemkie tehnologii i intellektualnyie sistemyi 2005[Technologies and Intelligent Systems 2005]. – Sb. nauchn. tr. VII Molodezhnoy NTK – Moskva: Izd-vo MGTU im N.E. Baumana. – 2005. – Pp.79 – 83. [in Russian]
8. Kwok P. Customizing thining algorithms/ P. Kwok // 3rt Int. Conf. Image Proc. and Appl., Warwik, 18 - 20 July. - 1989. - London. 1989. Pp.633-637.
9. Lure I., Kosikov A. Teoriya i praktika tsifrovoy obrabotki izobrazheniy [Theory and practice of digital image processing] . - M.: Nauchnyiy Mir. – 2003. – 176 p. [in Russian]
10. Miano D. Formatyi i algoritmyi szhatiya izobrazheniy v deystvii [Formats and algorithms for image compression in action]. – M.: Triumf. – 2003. – 336 p. [in Russian]