ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ РЕАКТИВНОЙ ЭЛЕКТРИЧЕСКОЙ МАШИНЫ ПРИ ПИТАНИИ ФАЗНЫХ ОБМОТОК СИНУСОИДАЛЬНЫМИ ФУНКЦИЯМИ ВРЕМЕНИ

Самосейко В.Ф.¹, Саушев А.В.², Тырва В.О.³, Широков Н.В.⁴, Шошмин В.А.⁵

¹Доктор технических наук, ²доктор технических наук, ³кандидат технических наук,

⁴кандидат технических наук,⁵доктор технических наук,

Государственный университет морского и речного флота (ГУМРФ) имени адмирала С.О. Макарова,

ЭЛЕКТРОМАГНИТНЫЙ МОМЕНТ РЕАКТИВНОЙ ЭЛЕКТРИЧЕСКОЙ МАШИНЫ ПРИ ПИТАНИИ ФАЗНЫХ ОБМОТОК СИНУСОИДАЛЬНЫМИ ФУНКЦИЯМИ ВРЕМЕНИ

Аннотация

Рассмотрены способы построения реактивных электрических машин. Предложена конструкция электрической машины с зубчатым статором и ротором, по фазным обмоткам которых протекают синусоидальные токи. Для формирования синусоидальных пульсаций индуктивностей обмоток статора предложена специальная геометрия поперечного сечения зубцов ротора, а также их аксиального скоса относительно зубцов статора. Получены выражения для номинальных значений угла нагрузки и электромагнитного момента по критерию размеров зубцовой зоны обмотки. Вычислены номинальные значения угла токовой нагрузки и электромагнитного момента при фиксированных размерах машины, заданных номинальных значениях плотности тока в катушках и магнитной индукции в зубцах статора.

Ключевые слова: реактивная электрическая машина, электромагнитный момент, угол токовой нагрузки.

Samoseyko V.F.¹, Saushev A.V.², Tyrva V.O.³, Shirokov N.V.⁴, Shoshmin V.A.⁵

¹PhD in Engineering, ²PhD in Engineering, ³PhD in Engineering, ⁴PhD in Engineering, ⁵PhD in Engineering,

Admiral Makarov State University of Maritime and Inland Shipping

ELECTROMAGNETIC MOMENT OF REACTIVE ELECTRIC MACHINE AT FEEDING OF PHASE WINDINGS WITH SINUSOIDAL TIME FUNCTIONS

Abstract

The ways of constructing reactive electric machines are considered. The design of the electric machine with a gear stator and rotor is proposed, with phase windings of sinusoidal currents flowing. A special geometry of the cross section of rotor teeth is proposed for the formation of sinusoidal pulsations of inductivities of stator windings, as well as their axial bevel with respect to stator teeth. Expressions are obtained for the nominal values of the load angle and the electromagnetic moment by the criterion of dimensions of the winding tooth zone. The nominal values of the angle of current load and the electromagnetic moment are calculated for the fixed machine dimensions, the nominal values of the current density in the coils and the magnetic induction in the stator teeth.

Keywords: reactive electric machine, electromagnetic moment, angle of current load.

Важнейшим элементом электропривода является электрическая машина. Наибольшее распространение в электроприводе получили синхронные и асинхронные машины переменного тока, принцип действия которых основан на пульсациях взаимных индуктивностей обмоток статора и ротора [1], [2]. В последние годы, в связи с развитием полупроводниковой преобразовательной техники, интерес представляют реактивные электрические машины, принцип действия которых основан на пульсациях собственных индуктивностей обмоток статора. Размах этих пульсаций определяет величину электромагнитного момента машины. Качество конструкции реактивной машины принято оценивать по отношению максимальной индуктивности, называемой продольной L_d, к минимальной индуктивности, называемой поперечной L_q. [3], [4].

Пульсаций индуктивностей обмоток статора можно добиться путем использования различных конструктивных решений ротора. Известны два конструктивных подхода к реализации роторов реактивных машин. Первый из них состоит в придании основанию цилиндра ротора зубчатой формы, а второй – в придании материала цилиндра ротора свойств, обуславливающих его анизотропную магнитную проводимость [5].

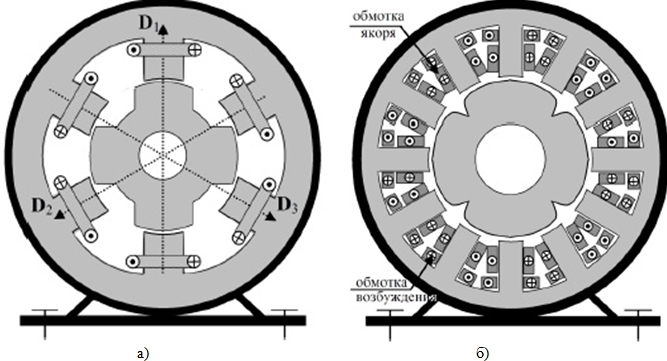
Машины с зубчатой формой ротора обычно используются в совокупности с сосредоточенными обмотками статора. Поэтому форма магнитопровода статора таких машин также имеет ярко выраженную зубчатую форму (Рис. 1а).

                                 

Рис. 1. – Магнитопровод реактивной 2-полюсной классической машины (а) и машины с пульсирующими по синусоидальному закону индуктивностями (б)

В настоящее время на рынок продвигаются электрические машины, которые используют импульсное питание фазных обмоток от вентильного коммутатора. Электрические машины с таким управлением в отечественной литературе обычно называются вентильно-индукторными [6], [7].

В отличие от классического подхода в статье рассматриваются реактивные электрические машины с зубчатым статором и ротором, по фазным обмоткам которых протекают синусоидальные токи.

В работах [4], [5], [8] показано, что целесообразно синтезировать конструкцию машины так, чтобы обеспечить условие постоянства электромагнитного момента, добиваясь синусоидального характера пульсаций индуктивностей фазных обмоток статора, а управление обмоткой осуществлять синусоидальными токами или синусоидальными токами с постоянной составляющей.

Машины с зубчатой формой основания цилиндра статора и ротора, которые требуют для питания токов синусоидальной формы с постоянной составляющей, будем называть индукторными. Машины, которые требуют для питания синусоидальных токов без постоянной составляющей, будем называть реактивными.

Добиться синусоидального характера пульсаций индуктивностей обмоток статора можно путем специальной геометрии поперечного сечения зубцов ротора, а также их аксиального скоса относительно зубцов статора [3]. Вид магнитопровода реактивной машины с пульсирующими по синусоидальному закону индуктивностями приведен на Рис. 1б.

Получим выражение для электромагнитного момента реактивной машины. Будем полагать, что по фазным обмоткам (катушкам) протекают синусоидальные токи

где I_d =I_acos(q_I); I_q =I_asin(q_I); I_a=(I_d²+I_q²)^1/2 — амплитудное значение тока в обмотке; q_I — угол токовой нагрузки; k=1,2,…,m — номера обмоток в порядке следования фаз; r=ep/m — угол фазового сдвига; e=1 при четном числе фаз и e=2 при нечетном числе фаз.

Индуктивности фазных обмоток пульсируют также как и магнитные проводимости по синусоидальному закону , где r=ep/m; k=1,…,m — электрические номера фазных обмоток. Кроме синусоидальной составляющей индуктивности обмоток имеют и высшие гармонические составляющие, которые обусловлены влиянием магнитопровода и геометрией воздушного зазора между статором и ротором

В m-фазных обмотках машины накапливается электромагнитная энергия, которая определяется выражением [4], [9]:

                                       (1)

где γ — электрическая угловая координата ротора.

Электромагнитная энергия может рассматриваться как потенциальная функция геометрической угловой координаты Г=2γ/Z_2, где Z₂ — число зубцов ротора. Тогда на ротор машины будет действовать электромагнитный момент

              (2)

Основная (постоянная) составляющая этого момента будет иметь вид:

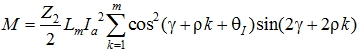                           (3)

где I_a — амплитуда силы тока катушки; L_m — амплитуда пульсаций индуктивности обмотки; q_I — угол токовой нагрузки; r — угол фазового сдвига. При числе фаз m>2 суммирование в формуле (3) по k дает следующее выражение основной составляющей электромагнитного момента:

                                                                 (4)

При числе фаз m=2 основная составляющая электромагнитного момента является пульсирующей функцией. При любом числе фаз m>1 среднее значение электромагнитного момента является постоянной величиной, определенной выражением (4). Если учесть связь токов обмотки с намагничивающей силой и индуктивностей обмотки с магнитной проводимостью обмотки:

 — число витков катушки, то получим:

                                                          (5)

где w — число витков обмотки; р — число пар полюсов; Ф₀=L_ddF_a — базовый магнитный поток; L_dd — продольная магнитная проводимость обмотки;  — удельная продольная магнитная проводимость обмотки; k_q — коэффициент поперечной магнитной проводимости; Z₁, Z₂ — число зубцов статора и ротора; F_a — амплитуда намагничивающей силы обмотки. При этом [4]:

где  – расчетный воздушный зазор;  – коэффициент выпучивания магнитного потока;  – угловой размер зубца статора.

Получим выражение для номинальных значений угла нагрузки и электромагнитного момента по критерию размеров зубцовой зоны обмотки. Будем полагать, что размеры этой зоны Z₁ определяются суммарной площадью сечения зубцов статора S_Z1 и суммарной площадью сечения пазов статора S_О. Пусть задано максимальное значение магнитной индукции в зубцах статора B_z1. Тогда базовое значение магнитного потока можно записать в следующем виде:

                                                        (6)

где Ф^*_zmax=Ф^*_zmax(q_I) – максимальное значение относительного магнитного потока через зубец статора;   – суммарная площадь сечения стали зубцов статора;  – относительная расчетная длина магнитопровода статора и ротора; γ₁ – коэффициент заполнения пакета статора сталью.

Амплитуду намагничивающей силы обмотки в выражении (5) представим в следующем виде [10]:

                                                                 (7)

где  – суммарная площадь, занимаемая проводниками в пазах статора;  – действующее значение плотности тока в проводниках; Z₁ – число зубцов статора;  – относительная высота зубцов статора;  – коэффициент заполнения паза медью;  – скважность зубцов статора; R – внутренний радиус магнитопровода статора.

Используя соотношения (6) и (7), представим электромагнитный момент (5) в следующем виде:

                                                                (8)

В формуле (8) функция 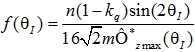 , где n – число пар зубцов ротора на полюсное деление статора; m – число фаз;  – коэффициент поперечной магнитной проводимости; θ_I – угол токовой нагрузки.

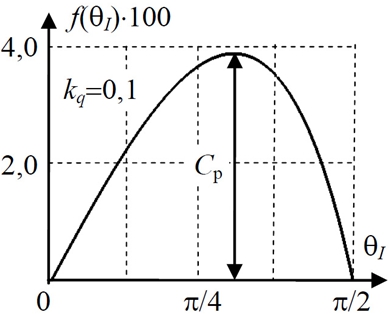
Вычислим номинальное значение угла токовой нагрузки. При фиксированных размерах машины, заданных номинальных значениях плотности тока в катушках и магнитной индукции в зубцах статора, функция f(θ_I) определяет с точностью до постоянного множителя зависимость электромагнитного момента в функции от угла токовой нагрузки. График функции f(θ_I) приведен на Рис. 2 номинальное значение угла токовой нагрузки принимается его значение , при котором функция f(θ_I) имеет максимальное значение .

Номинальное значение электромагнитного момента определяется по формуле (8) при номинальном значении угла токовой нагрузки θ_I:

где  — действующее значение плотности тока в проводниках;  — максимальное значение магнитной индукции в зубцах статора;  — суммарная площадь пазов;  — суммарная площадь сечения стали зубцов статора.

Рис. 2. – График функции f(θ_I)

Полученные формулы позволяют рассчитать значения электромагнитного момента реактивной индукторной электрической машины, питаемой синусоидальными токами, а также вычислить номинальное значение угла токовой нагрузки машины. Они являются основой для проектирования реактивных электрических машин с зубчатой формой основания цилиндра статора и ротора.

Список литературы / References

1. Самосейко В. Ф. Теоретические основы управления электроприводом / В. Ф. Самосейко. – СПб.: Элмор, 2007. – 464 с.
2. Саушев А.В. Основы электромеханического преобразования энергии / А. В. Саушев. – СПб: СПГУВК, 2012. – 246 с.
3. Самосейко В.Ф. К теории индуктивных явнополюсных электрических машин / В. Ф. Самосейко // «Электричество». – 2009. – №11. – С.38 – 47.
4. Самосейко В. Ф. Реактивные электрические машины с зубчатым статором и ротором. Методика проектирования. Алгоритмы управления / В. Ф. Самосейко, Ф. А. Гельвер, В. А. Хомяк, Н. А. Лазаревский – СПб.: Изд. Крыловский государственный научный центр, 2016. – 197 с.
5. Самосейко В. Ф. Синхронная машина с анизотропной магнитной проводимостью ротора / В. Ф. Самосейко, Ф. А. Гельвер, В. А. Хомяк // Труды Крыловского государственного научного центра. – 2014. – Вып. 81 (365). – С. 143 – 150.
6. Самосейко В.Ф. Реактивные электрические машины в электроприводе транспортных машин и механизмов / В. Ф. Самосейко, А. В. Саушев // Сборник докладов научно-технического семинара «Электропривод в транспорте».– М.: МЭИ, 2017. – С. 49 – 54.
7. Самосейко В.Ф. Перспективы применения реактивных электрических машин в электроприводе / В. Ф. Самосейко, А. В. Саушев // Science in the modern information society XII. Vol. 1: Proceedings of the Conference. North Charleston, 19-20.06.2017, Vol. 1–North Charleston, SC, USA: CreateSpace, 2017, P. 66 – 69.
8. Самосейко В. Ф. Анализ преимуществ реактивных электрических машин при построении гребной электрической установки / В. Ф. Самосейко, С. В. Шарашкин // Вестник ЮУрГУ. Сер. Энергетика. – 2017. – № 2. – С. 14–22.
9. Григорьев М. А. Предельные возможности электроприводов с синхронной реактивной машиной независимого возбуждения и с другими типами двигателей / М. А. Григорьев // Вестник ЮУрГУ. Сер. Энергетика. – 2009. – № 12. – С. 51 – 55.
10. Chang-Chou H. Optimal Design of an SPM Motor Using Genetic Algorithms and Taguchi Method / H. Chang-Chou, L. Li-Yang, L. Cheng-Tsung, L. Ping- Lun // IEEE Trans. on Magn. 44(2008). – 2008. – № 11. – Р. 4325–4328.

Список литературы на английском языке / References in English

1. Samoseyko V. F. Teoreticheskie osnovy upravlenija jelektroprivodom [Theoretical bases of control of the electric drive] / V.F. Samosejko. – SPb.: Jelmor, 2007. – 464 P. [in Russian]
2. Saushev A.V. Osnovy jelektromehanicheskogo preobrazovanija jenergii [Bases of electromechanical conversion of energy] / A.V. Saushev. – SPb. SPGUVK, 2012. – 246 P. [in Russian]
3. Samoseyko V. F. K teorii induktivnyh javnopoljusnyh jelektricheskih mashin [To the theory of the inductive salient pole electrical machines] / V. F. Samosejko // Jelektrichestvo [Electricity]. – 2009. – №11. – p. 38 – 47. [in Russian]
4. Samoseyko V. F. Reaktivnye jelektricheskie mashiny s zubchatym statorom i rotorom. Metodika proektirovanija. Algoritmy upravlenija [Reluctance electrical machines with the toothed stator and a rotor. Design technique. Control algorithms] / V. F. Samosejko, F. A. Gel'ver, V.A. Homjak, N. A. Lazarevskij - SPb.: Izd. Krylovskij gosudarstvennyj nauchnyj centr [Prod. Krylov state scientific center], 2016. – 197 P [in Russian]
5. Samoseyko V. F. Sinhronnaja mashina s anizotropnoj magnitnoj provodimost'ju rotora [The synchronous machine with anisotropic magnetic conductance of a rotor] / V. F. Samosejko, F. A. Gel'ver, V. A. Homjak // Trudy Krylovskogo gosudarstvennogo nauchnogo centra [Works of Krylov state scientific center] – 2014. – Vyp. 81 (365). – p. 143 – 150. [in Russian]
6. Samoseyko V. F. Reaktivnye jelektricheskie mashiny v jelektroprivode transportnyh mashin i mehanizmov [Reluctance electrical machines in the electric drive of transport vehicles and mechanisms] / V. F. Samosejko, A. V. Saushev // Sb. dokl. nauchno-tehnicheskogo seminara "Jelektroprivod v transporte" [The collection of reports of a scientific and technical seminar «The electric drive in transport»]. - M.: MEI, 2007. – p. 49 – 54. [in Russian].
7. Samosejko V. F. Perspektivy primenenija reaktivnyh jelektricheskih mashin v jelektroprivode [Perspectives of use of reluctance electrical machines in the electric drive] / V. F. Samosejko, A. V. Saushev / Science in the modern information society XII. Vol. 1: Proceedings of the Conference. North Charleston, 19-20.06.2017, Vol. 1–North Charleston, SC, USA: CreateSpace, 2017, p. 66 – 69.
8. Samosejko V. F. Analiz preimushhestv reaktivnyh jelektricheskih mashin pri postroenii grebnoj jelektricheskoj ustanovki [The analysis of advantages of reluctance electrical machines at creation of the rowing electrical unit] / V. F. Samosejko, S. V. Sharashkin // Vestnik JuUrGU. Ser. Jenergetika [the Messenger of YuurGU. It is gray. Power engineering]. – 2017. – №. 2. – p. 14 – 22. [in Russian]
9. Grigor'ev M. A. Predel'nye vozmozhnosti jelektroprivodov s sinhronnoj reaktivnoj mashinoj nezavisimogo vozbuzhdenija i s drugimi tipami dvigatelej [Limit opportunities of electric drives with the synchronous reluctance machine of independent excitation and with other types of engines] / M. A. Grigor'ev // Vestnik JuUrGU. Ser. Jenergetika [the Messenger of YuurGU. It is gray. Power engineering]. – 2009. – №. 12. – p. 51 – 55. [in Russian]
10. Chang-Chou H. Optimal Design of an SPM Motor Using Genetic Algorithms and Taguchi Method / H. Chang-Chou, L. Li-Yang, L. Cheng-Tsung, L. Ping- Lun // IEEE Trans. on Magn. 44(2008). – 2008. – № 11. – Р. 4325–4328.