ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ГЛОБОИДНОГО ЗАЦЕПЛЕНИЯ С УЧЕТОМ ИЗНОСА
Вяткин А.И.
Кандидат технических наук, Тюменский государственный университет
ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКОЙ МОДЕЛИ ГЛОБОИДНОГО ЗАЦЕПЛЕНИЯ С УЧЕТОМ ИЗНОСА
Аннотация
В статье предложена схема расчета полей зазоров в зацеплении элементов глобоидной передачи, учитывающая накопленный износ витка червяка, зуба колеса и пластические деформации, возникающие при нагрузке на колесо. Изменение формы контактирующих поверхностей предложено учитывать с помощью алгоритма, реализуемого в три этапа. На первом этапе решается задача о положениях в глобоидном зацеплении с абсолютно жесткими звеньями, дающая исходную матрицу зазоров. На втором этапе решается задача нахождения формы и положения площадок контакта неизнашивающихся сопряженных поверхностей с учетом пластических деформаций. Третий этап разработанного алгоритма предусматривает численное моделирование дискретизированного процесса износа зацепления.
Ключевые слова: матрица зазоров, износ, фаза зацепления, пластические деформации.
Vyatkin A.I.
Assistant professor, PhD in Engineering
Tyumen State University
DEVELOPMENT OF GLOBOID TRANSMISSION GEOMETRIC MODEL WITH REGARD TO DEPRECIATION
Abstract
The article suggests a scheme for calculating gaps margins in the engagement of globoid transmission elements with an account of accumulated depreciation of a worm round and a wheel tooth, as well as plastic deformations resulting from the load on the wheel. The article suggests taking account of a change in the form of contacting surfaces with the help of an algorithm implemented in three stages. At the first step we solve the problem of positions in globoid engagement with absolutely rigid links, which gives the original gaps matrix. At the second stage we deal with the problem of finding the shape and the position of the contact pads of wear-free mating surfaces with an account of plastic deformations. The third stage of the developed algorithm provides the numerical modeling of sampled engagement depreciation process.
Keywords: gaps matrix, depreciation, engagement phase, plastic deformation.
В связи с изменением формы контактирующих поверхностей в рассмотренной ранее расчетной схеме глобоидного зацепления изменяется их относительное положение и, как следствие, изменяются положение контактной точки, значения геометрических, кинематических и силовых характеристик контакта. Это приводит к необходимости решать сложные сами по себе и разнородные по применяемым методам задачи определения указанных выше величин на каждом шаге износа, что существенно затрудняет решение и увеличивает время расчета. Сложность решения усугубляется рядом особенностей глобоидного зацепления, в частности тем, что из-за высокой плотности контакта даже малые изменения формы сопряженных поверхностей могут приводить к значительному изменению положения, формы и размеров площадки контакта.
Как было показано в работе [1], трудности при нахождении геометрических и кинематических характеристик распределения нагрузки между зубьями колеса и витками червяка, а также давлений по площадкам контакта могут быть преодолены с помощью единого итерационного алгоритма решения задачи об относительном положении колеса и червяка. Данный алгоритм основывается, в конечном итоге, на определении зазоров в каждом цикле расчета между сопряженными поверхностями.
Нетрудно показать, что изменение формы сопряженных поверхностей также может быть учтено на основе аналогичного алгоритма. Действительно, изменение формы поверхностей при выбранной дискретной модели процесса износа происходит мгновенно, в конце шага износа и, следовательно, в фиксированной фазе зацепления.
Поэтому изменение формы поверхностей может быть учтено корректировкой положения колеса относительно червяка и сведено к упомянутой выше задаче о положениях.
Изменение формы контактирующих поверхностей предложено учитывать с помощью алгоритма, реализуемого в три этапа.
На первом этапе решается задача о положениях в глобоидном зацеплении с абсолютно жесткими звеньями. Решение ведется с учетом особенностей и погрешностей схем формообразования зубьев колеса и витков червяка, погрешностей монтажа, с использованием аппарата теории зубчатых зацеплений. Для каждого оптированного положения червяка отыскиваются координаты точек касания сопряженных поверхностей и значения угла поворота колеса, соответствующие выбранному положению червяка. В этом положении вычисляются зазоры между сопряженными поверхностями в узлах сеток, построенных на поверхностях. При этом за основу бралась схема, предложенная А.В.Бондаренко [1], которую логично проиллюстрировать следующим образом.
Если червяк и зуб колеса рассечь одновременно плоскостью, перпендикулярной оси колеса, и цилиндром, соосным оси колеса, то в результате мы получаем две точки: точку t - принадлежащую витку червяка и точку Р - принадлежащую боковой поверхности зуба колеса (рис.1). Расстояние между этими точками, измеренное по дуге секущего цилиндра, и дает нам зазор между витком червяка и зубом колеса в данной узловой точке. Если же рассечь оба элемента зацепления несколькими цилиндрами радиусом Ri и плоскостями Вi. - получим поле зазоров, по которому судим о характере и месте контакта витка червяка и зуба колеса. Поля зазоров рассчитывались для четырех положений червяка (через 90 градусов) относительно червячного колеса. Максимальное количество зубьев в зацеплении определялось теоретически по углу обхвата. Поскольку в рассматриваемом зацеплении одновременно находилось от четырех до пяти зубьев колеса, было получено 17 полей первоначальных зазоров.
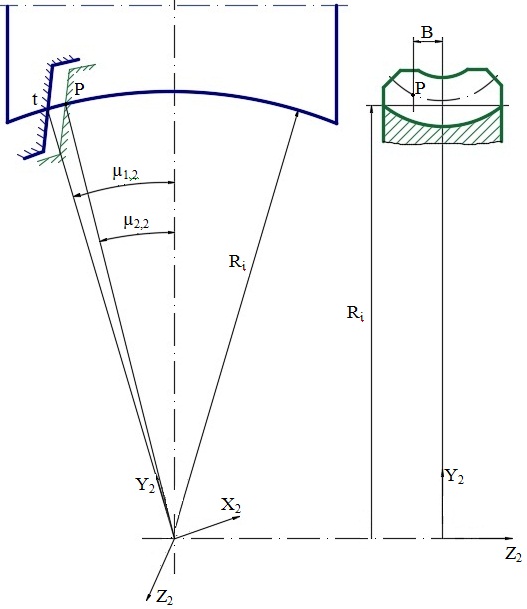
Рис. 1 – Схема определения зазоров между элементами глобоидной пары
На рис. 2 (1 – червяк, 2 - колесо) приведено одно из фиксированных положений червяка и колеса с соответствующими параметрами фаз зацепления µim до износа: µ1,2 = -675°, µ1,6= -315°, µ1,10= 45°, µ1,14= 405°.
На втором этапе решаются задачи нахождения формы и положения площадок контакта неизнашивающихся сопряженных поверхностей, их числа для заданной величины внешнего момента и определения контактных давлений в расчетных точках. За расчетные точки принимаются узловые точки, находящиеся в пределах площадок контакта.
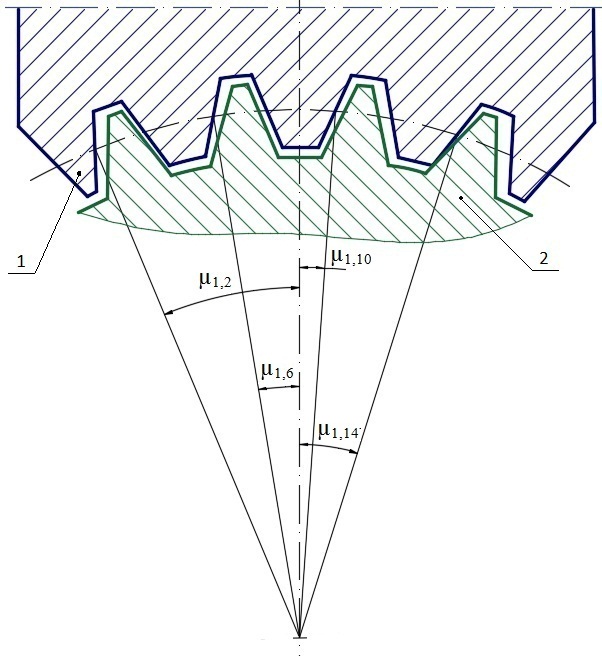
Рис. 2 – Схема контакта элементов глобоидной пары
При этом учитывается деформация элементов передачи, в том числе контактные и изгибно-сдвиговые деформации зубьев колеса и витков червяка. В конце рассматриваемого этапа определяется новое положение колеса относительно червяка, для этого положения вычисляются зазоры в узловых точках сопряженных поверхностей, и корректируется матрица исходных зазоров.
Решение задач первого и второго этапа базируется на модернизированных итерационных алгоритмах, разработанных ранее [1] для оценки нагруженности глобоидного зацепления. Модернизация потребовалась для учета пластических деформаций, которые могут возникать в расчетных узловых точках.
Третий этап разработанного алгоритма предусматривает численное моделирование дискретизированного процесса износа зацепления. Для нахождения величин износа в узловых точках поверхностей зубьев колеса и витков червяка заданная длительность процесса функционирования зацепления делится на периодически повторяющиеся циклы, каждый из которых, в свою очередь, разделяется на целое число шагов износа. Предполагается, что в начале первого шага износа сопряженные поверхности не изношены, их относительное положение определяется результатами расчета на предыдущем этапе алгоритма. В соответствии с этим считаются известными координаты узловых точек и матрица зазоров для них, а также данные о том, какие именно из них являются расчетными и контактные давления в последних. Если считать, что аналогичная информация, учитывающая изменение всех факторов на предыдущих шагах износа, имеется в начале n-го шага, то величину износа ∆hi,j в конце этого шага можно определить с помощью зависимостей (1) и (2).
∆hi,j = Ji,j∆Li,j (1)
где i,j - индексы, соответствующие положению контактной точки на поверхностях зуба колеса и витка червяка; ∆Li,j - путь трения для выбранной точки зуба колеса (витка червяка); Ji,j - интенсивность износа материала зубьев колеса (витка червяка) на данном шаге расчета износа.
Ji,j = K12Pij /HB (2)
где Pij - нормальное контактное давление в той же точке; НВ - твердость материала зубьев колеса или витков червяка [2].
После определения матриц зазоров во всех фазах, для обеспечения контакта поверхности витка с зубьями колеса после текущей итерации по износу, необходимо было компенсировать увеличение зазоров за счет учета пластических деформаций и износа путем доворота колеса, величина которого определялась в следующей последовательности. Общая величина зазора в текущий момент времени в период приработки передачи без учета доворота колеса определялась по формуле:
∆mij= Wmij + Н1ij + Н2ij.+ δпл , (3)
где Wmij - первоначальный зазор до износа сопряжения, мм;
Н1ij, Н2ij - накопленный износ витка червяка и зуба колеса в рассматриваемой узловой точке сетки, мм;
δпл - пластическая деформация, мм.
Угол доворота колеса находился в виде:
∆φnij = ∆mij / Rij (4)
где n - номер фиксированного положения червяка и колеса;
Rij - радиус секущей окружности для рассматриваемой узловой точки
сетки, мм.
Реальный зазор в узловой точке сетки в текущий момент наработки рассчитывался так:
∆mij= (∆φnij - ∆φmin) Rij (5)
где ∆φmin - минимальный угол доворота колеса, выбранный по величине ∆φnij для рассматриваемого фиксированного положения червяка и колеса.
Вновь полученная матрица зазоров являлась исходной для следующей итерации по расчету износа и характеризовала на данном временном шаге изменение геометрии.
Таким образом, решается задача изменения формы поверхностей зацепления в процессе работы глобоидной передачи.
Список литературы / References
- Бондаренко А.В. Статическая нагруженность глобоидного зацепления с учетом особенностей формообразования, погрешностей изготовления, монтажа и податливости элементов передачи. : дис.… канд. тех.наук : 05.02.02 :защищена 12.06.87 : утв. 16.09.87 / Бондаренко Александр Васильевич. – Курган, 1987. – 353 с.
- Хрущов М.М., Бабичев М.А. Исследование изнашивания металлов. - М.: АН СССР, 1960. – 64 с.
Список литературы на английском языке / References in English
- Bondarenko A.V. Staticheskaya nagruzhennost' globoidnogo zacepleniya s uchetom osobennostej formoobrazovaniya, pogreshnostej izgotovleniya, montazha i podatlivosti ehlementov peredachi [Static loading of globoid engagement with an account of peculiarities of forming, fabrication errors, installation and compliance of the transmission elements] : dis. … of PhD in Engineering : 05.02.02. : defense of the thesis 12.06.87: approved 16.09.87 / Bondarenko Aleksandr Vasil'evich. – Kurgan, 1997. – 220 p. [in Russian]
- Khrushchov M.M., Babichev M.A. Issledovanie I znashivaniya metallov [Metal depreciation study] / M.M. Krushchov, M.A. Babichev. – M : AN SSSR, 1960. – 64 p. [in Russian]
