ОБОБЩЕННЫЕ ВАРИАНТЫ УПРАВЛЕНИЯ МНОГОФАЗНЫМИ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ ПЕРЕМЕННОГО ТОКА

Григорьев А.В.

ORCID: 0000-0001-7429-3174, Кандидат технических наук, Кузбасский государственный технический университет имени Т.Ф. Горбачева

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 16-38-00929 мол_а)

ОБОБЩЕННЫЕ ВАРИАНТЫ УПРАВЛЕНИЯ МНОГОФАЗНЫМИ ЭЛЕКТРИЧЕСКИМИ МАШИНАМИ ПЕРЕМЕННОГО ТОКА

Аннотация

Приведена модель многофазной электрической машины с произвольным числом фазных обмоток статора и ротора в форме пространства состояний. Предложенная модель позволяет исследовать несимметричные режимы работы многофазной электрической машины, что является достоинством в сравнении с моделью на основе симметричных составляющих. На основе модели в форме пространства состояний выполнен синтез оптимальных управляющих устройств в смысле быстродействия электроприводом на базе многофазной электрической машины и многофазного мостового инвертора напряжения при помощи принципа максимума Л.С. Понтрягина. Синтезированные конструкции оптимальных управляющих устройств позволяют простыми преобразованиями получить правила формирования управляющих воздействий с целью стабилизации любой переменной электропривода, зависящей от потокосцеплений фазных обмоток двигателя.

Ключевые слова: многофазный электродвигатель, обобщенные конструкции, оптимальное управление, принцип максимума Л.С. Понтрягина.

Grigorev A.V.

ORCID: 0000-0001-7429-3174, PhD in Engineering, Kuzbass State Technical University of T.F. Gorbachev

GENERIC OPTIONS OF MANAGING MULTI-PHASE ELECTRIC MACHINE WITH AC

Abstract

A model of multi-phase electric machine with a random number of phase windings of the stator and rotor in the form of space states is provided. Proposed model allows us to investigate asymmetric working modes of a multi-phase electric machine, which is an advantage in comparison with the model based on symmetrical components. We conducted synthesis of optimal control devices on the basis of the model in state space form in terms of the performance of electric poly-phase based on electric machines and a multi-phase bridge voltage inverter by means of the maximum principle of L.S.Pontryagin. Synthesized design of optimal control devices allows obtaining rules for the control actions by means of simple transformations in order to stabilize electric variables that depend on the flux linkage in phase motor winding.

Keywords: multiphase electric motor, generalized expressions, optimal control, maximum principle of  L.S. Pontryagin.

Вопросами управления электроприводами на базе многофазных электрических машин переменного тока занимается много авторов. Основным направлением является адаптация методов управления, полученных для обобщенной электрической машины (векторные способы управления [2, С. 1178], варианты прямого управления моментом [4, С. 1] и другие [3, С. 13]), к многофазной машине переменного тока при помощи фазных преобразований. Ряд авторов обращает свое внимание на получение общих принципов адаптации известных способов управления к многофазной электрической машине, например, в работе [1, С. 570] представлены общие принципы адаптации способов векторного управления к шестифазным электрическим машинам с двумя обмотками статора (Dual Six-Phase Motor). В работе [4, С. 4] получена обобщенная таблица оптимальных переключений ключей инвертора для варианта управления DTC применительно к многофазной электрической машине, не учитывающая, однако, величину отклонения текущих значений электромагнитного момента и потокосцепления статора. Таким образом, проблема получения обобщенных вариантов управления многофазными электрическими машинами с произвольным числом фазных обмоток является актуальной.

Принципиальная электрическая схема многофазной электрической машины с числом фазных обмоток на статоре и роторе, равном n, показана на рис. 1.

В работах [5, С. 62], [6, С. 40], [7, С. 155] приводится процедура синтеза оптимальных управляющих устройств для обобщенной электрической машины и трехфазной асинхронной электрической машины, получающих питание от автономных инверторов напряжения.

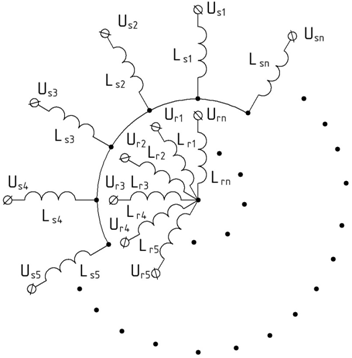
Рис. 1 – Принципиальная электрическая схема многофазной электрической машины: L_s1..n, L_r1..n – индуктивности обмоток статора и ротора; U_s1..n, U_r1..n – фазные напряжения, подаваемые на обмотки статора и ротора

Для применения данной процедуры к синтезу управляющих устройств многофазной электрической машиной, получающей питание от автономного многофазного инвертора напряжения, необходимо представить математическую модель многофазной машины в форме пространства состояний. В качестве координат фазового пространства удобно взять потокосцепления фазных обмоток статора и ротора. Тогда обобщенная модель многофазной симметричной электрической машины может быть представлена следующим образом:

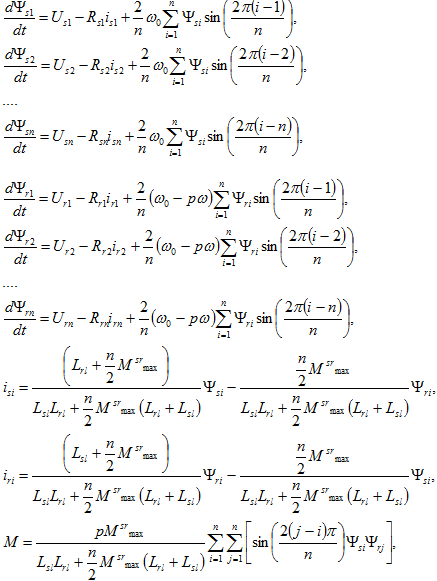  (1)

где n – число фаз статора и ротора; p – число пар полюсов обмоток статора и ротора; ω₀ – круговая частота вращения системы координат, в которой представлены координаты фазового пространства; ω – круговая частота вращения ротора электродвигателя; Ψ_si, Ψ_ri – потокосцепления i-ых фазных обмоток статора и ротора;  i_si, i_ri – токи i-ых фазных обмоток статора и ротора; R_si, R_ri – активные сопротивления i-ых фазных обмоток статора и ротора; L_sl, L_rl – индуктивности рассеяния фазных обмоток статора и ротора; M ^sr_max – максимальное значение взаимной индуктивности между обмотками статора и ротора; M – электромагнитный момент двигателя.

Указанная модель (1) получена при следующих допущениях: обмотки статора и ротора представляют собой токовые слои, уложенные равномерно на поверхностях статора и ротора, а магнитодвижущие силы, создаваемые этими токовыми слоями, распределены по окружности статора и ротора по косинусоидальному закону; зазор машины равномерен; сталь машины не насыщается, и в машине отсутствуют магнитные потери; индуктивности рассеяния фазных обмоток равны и постоянны; максимальные взаимные индуктивности любой пары фазных обмоток равны M ^sr_max.

Решение задачи управления можно получить при помощи принципа максимума Л.С. Понтрягина [8, С. 235]. Цель задачи синтеза управления представим в следующем виде:

где  - целевая функция; Y, Y^* - векторы текущих и заданных значений фазовых координат или значений функций от фазовых координат; Ψ_s, Ψ_r – векторы потокосцеплений фазных обмоток статора и ротора.

Для достижения поставленной цели необходимо сформировать следующую вспомогательную функцию:

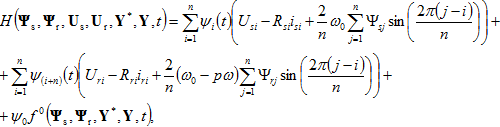
где ψ_i – i-ая составляющая вектор-функции ψ(t).

Для определения компонент вектор-функции ψ(t) необходимо решить следующую сопряженную систему уравнений:

Решение представленной системы уравнений совместно с системой уравнений (1) представляется довольно громоздким и требует задания начальных условий (для задач электропривода это невыполнимо), поэтому дополнительно необходимо еще использовать условия трансверсальности [8, C. 327]: вектор-функция ψ должна быть ортогональна всем возможным векторам в гиперплоскости, касательной к начальному и конечному многообразию. Это означает, что вектор ψ является нормалью указанной гиперплоскости и задается выражением:

где φ(x) – функция вектора фазовых координат x, задающая гиперповерхность.

Поскольку в данной работе рассматривается задача перевода объекта из состояния x₀, при котором Y = Y₀ в состояние x₁, при котором Y = Y^*, то начальное и конечное многообразия задаются не системой уравнений (1), а целевой функцией f ⁰. Отсюда следует, что компоненты вектор-функции ψ определяются при помощи следующих более простых соотношений:

Условие максимума функции  H приводит к необходимости выполнения следующих требований к управляющим воздействиям для того, чтобы процесс был оптимальным в смысле быстродействия:

  (2)

Если управляющие воздействия не зависимы, то условие (2) выполняется при выполнении следующих условий:

 (3)

Следует отметить, что в электроприводе зачастую используют мостовой инвертор напряжения, на выходе которого формируются фазные напряжения, зависящие от состояния каждого силового ключа (см. рис. 2). Если обозначить через S_i – состояния ключей инвертора, где S_i = 1 соответствует открытому верхнему ключу (VT1, VT3.. VT(n-1)) полумоста инвертора, а S_i = 0 соответствует открытому нижнему ключу (VT2, VT4.. VTn) полумоста инвертора, то фазные напряжения, формируемые инвертором, можно кратко записать в следующем виде:

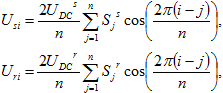
где индексы ^s, ^r – означают принадлежность к питающим цепям статора и ротора, соответственно; U_DC – напряжение шины постоянного тока мостового инвертора.

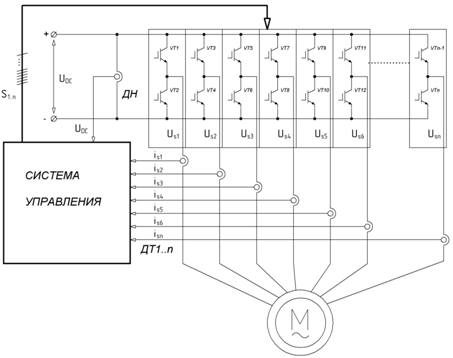
Рис. 2 – Многофазный инвертор, подключенный к многофазной электрической машине

 

Из выражений (4) следует, что управляющие воздействия, подаваемые на фазные обмотки статора, зависят друг от друга, а значит, для определения алгоритма формирования управляющих воздействий, можно применять только более сильное условие (2).

Подставив выражения (4) в условие (2), получим следующие условия, на базе которых можно получить алгоритм формирования управляющих воздействий:

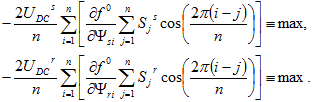  (5)

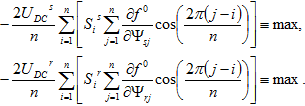Условия (5) эквивалентны следующим условиям:    (6)

Из условий (6) следует обобщенный алгоритм формирования управляющих воздействий на мостовые инверторы напряжения, питающие многофазную электрическую машину:

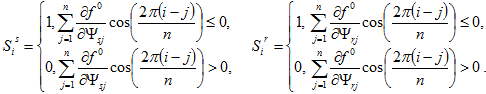  (7)

Выражения (7) являются основной частью обобщенного алгоритма формирования управляющих воздействий, обеспечивающего стремление к минимуму целевой функции f⁰. В случае стабилизации какой-либо переменной электродвигателя в качестве данной функции может выступать квадратичная форма отклонения текущего значения переменной от заданного:

где y, y^* – текущее и заданное значения стабилизируемой переменной электродвигателя.

Таким образом, в данной работе были получены обобщенные конструкции управляющих устройств многофазной электрической машиной, получающей питание от инвертора напряжения, не требующие выполнения фазных преобразований и декомпозиции управляющих векторов. В дальнейших исследованиях планируется рассмотреть варианты управления многофазными электрическими машинами, получаемые при подстановке в целевые функции квадратичных форм отклонений текущих значений потокосцепления статора и электромагнитного момента от заданных.

Список литературы / References

1. Zhao Y. Modeling and Control of Multi-Phase Induction Machine with Structural Unbalance / Y. Zhao, T. A. Lipo // IEEE Transactions on Energy Conversion. – 1996. – V. 11. – № 3. – P. 570–577.
2. Sigh G. K. A Simple Indirect Field-Oriented Control Scheme for Multiphase Induction Machine / G. K. Sigh, K. Nam, S. K. Lim // IEEE Transactions On Industrial Electronics. – 2005. – V. 52. – №4. – P. 1177–1184.
3. Taheri A. Speed Sensor-Less Estimation and Predictive Control of Six-phase Induction Motor Using Extended Kalman Filter / A. Taheri, M. Mohammadbeigi // The 5th Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014). – 2014. – P. 13–18.
4. Karampuri R. Extension of the DTC Technique to Multiphase Induction Motor Drives using any Odd Number of Phases / R. Karampuri, J. Prieto, F. Barrero, S. Jain // IEEE Vehicle Power and Propulsion Conference (VPPC 2014). – 2014. – P. 1–6.
5. Ещин Е. К. Задача управления электромагнитным моментом асинхронного электродвигателя – прямое управление моментом / Е. К. Ещин // Вестник КузГТУ. – 2006. – №6 (2). – С. 61–63.
6. Ещин Е. К. Общая задача управления асинхронным электродвигателем / Е. К. Ещин, А. В. Григорьев // Известия вузов. Электромеханика. – 2010. – №1. – С. 39–43.
7. Григорьев А. В. Управление электромагнитным моментом электропривода на базе трехфазного асинхронного электродвигателя / А. В. Григорьев // Известия Томского политехнического университета. – 2012. – №4. – С. 154–158.
8. Болтянский В. Г. Математические методы оптимального управления / В. Г. Болтянский. – 2-е изд., перераб. и доп. – М.: Наука: Главная ред. физ.-мат. лит., 1968. – 408 с.

Список литературы на английском языке / References in English

1. Zhao Y. Modeling and Control of Multi-Phase Induction Machine with Structural Unbalance / Y. Zhao, T. A. Lipo // IEEE Transactions on Energy Conversion. – 1996. – V. 11. – №3. – P. 570–577.
2. Sigh G. K. A Simple Indirect Field-Oriented Control Scheme for Multiphase Induction Machine / G. K. Sigh, K. Nam, S. K. Lim // IEEE Transactions On Industrial Electronics. – 2005. – V. 52. – №4. – P. 1177–1184.
3. Taheri A. Speed Sensor-Less Estimation and Predictive Control of Six-phase Induction Motor Using Extended Kalman Filter / A. Taheri, M. Mohammadbeigi // The 5th Power Electronics, Drive Systems and Technologies Conference (PEDSTC 2014). – 2014. – P. 13–18.
4. Karampuri R. Extension of the DTC Technique to Multiphase Induction Motor Drives using any Odd Number of Phases / R. Karampuri, J. Prieto, F. Barrero, S. Jain // IEEE Vehicle Power and Propulsion Conference (VPPC 2014). – 2014. – P. 1–6.
5. Eshchin E. K. Zadacha upravleniya ehlektromagnitnym momentom asinhronnogo ehlektrodvigatelya – pryamoe upravlenie momentum [The problem of the electromagnetic torque of an induction motor control – direct torque control] / E. K. Eshchin // Vestnik KuzGTU [The messenger of KuzSTU]. – 2006. – V. 2. – №6. – P. 61–63. [in Russian]
6. Eshchin E. K. Obshchaya zadacha upravleniya asinhronnym ehlektrodvigatelem [The general problem of an induction motor control] / E. K. Eshchin, A. V. Grigor'ev // Izvestiya vuzov. EHlektromekhanika [News of universities. Electromechanics]. – 2010. – №1. – 39–43. [in Russian]
7. Grigor'ev A. V. Upravlenie ehlektromagnitnym momentom ehlektroprivoda na baze trekhfaznogo asinhronnogo ehlektrodvigatelya [An electrical drive based on three-phase asynchronous motor control] / A. V. Grigor'ev // Izvestiya Tomskogo politekhnicheskogo universiteta [News of Tomsk polytechnic university]. – 2012. – №4. – P. 154–158. [in Russian]
8. Boltyanskij V. G. Matematicheskie metody optimal'nogo upravleniya [Mathematical methods of the optimal control theory] / V. G. Boltyanskij. – 2-e izd., pererab. i dop. – M.: Nauka: Glavnaya red. fiz.-mat. lit., 1968. – 408 p. [in Russian]