О КОРРЕКТНОСТИ ОБРАТНЫХ ЗАДАЧИ ОПРЕДЕЛЕНИЯ ПАРЫ {u, σ}, В СЛУЧАЕ ПРОСТОЙ ОБЛАСТИДЛЯ УРАВНЕНИЯ ПЕРЕНОСА ИЗЛУЧЕНИЙ

Сариев А.Д.¹, Шаждекеева Н.К.², Шыганакова А.Т.³, Каракенова С.Г.⁴, Сариев С.Д.⁵

¹ORCID: 0000-0002-1825-0023, Кандидат физико-математических наук, Атырауский государственный университет в г. Атырау, ²ORCID: 0000-0002-1825-0023, Кандидат физико-математических наук,Атырауский государственный университет в г. Атырау, ³ORCID: 0000-0002-1825-0097, Магистр математики, Атырауский государственный университет в г. Атырау, ⁴ORCID: 0000-0002-1825-0097, Магистр математики, Атырауский государственный университет в г. Атырау, ⁵ORCID: 0000-0002-1825-0097, Магистр математики, Международный казахско-турецский университет, г. Туркестан

О КОРРЕКТНОСТИ ОБРАТНЫХ ЗАДАЧИ ОПРЕДЕЛЕНИЯ ПАРЫ {u, σ}, В  СЛУЧАЕ ПРОСТОЙ ОБЛАСТИ ДЛЯ УРАВНЕНИЯ ПЕРЕНОСА ИЗЛУЧЕНИЙ

Аннотация

В статье изложены основные вопросы исследования локальных свойств интеграла столкновений и классического решения нестационарного уравнения переноса излучения, рассматриваемого в простой области из R₃.

В статье изучены и доказаны вопросы корректности «в целом» ряда обратных задач для нестационарного уравнения переноса, рассматриваемого в ограниченной простой области из R_3, для одновременного определения пары {u, σ}.

Приводится гладкость рассматриваемой области,  учитывая  простату области, доказаны  лемма 1-4, на основе этих лемм доказано теорема 1.

Ключевые слова: уравнение переноса, локальные свойства, интеграл столкновений, односкоростное нестационарное уравнение, начальное условие, граничное условие, вопросы корректности решения, ограниченная простая область из R₃.

SarievA.D.¹, Shazhdekeyeva N.K.², Shyganakova A.T.³, Karakenova S.G.⁴, Sariev S.D.⁵

¹ORCID: 0000-0002-1825-0023, PhD in candidate physics - mathematics science, Atyrau State University, ²ORCID: 0000-0002-1825-0023, PhD in candidate physics - mathematics science,Atyrau State University, ³ORCID: 0000-0002-1825-0097, Master of mathematics,Atyrau State University, ⁴ORCID: 0000-0002-1825-0097, Master of mathematics,Atyrau State University, ⁵ORCID: 0000-0002-1825-0097, Master of mathematics,International Kazakh-Turkish University, Turkestan

ON THE CORRECTNESS OF INVERSE PROBLEM OF DETERMINING COUPLE {u, σ} IN THE CASE OF A SIMPLE EQUATION FOR THE TRANSFER OF RADIATION

Abstract

The article outlines the main research questions of the local properties of the collision integral and classical solutions of non-stationary radiative transfer equation, considered in the plain area of R₃.

The paper studied and proved the correctness of questions "in the large" number of inverse problems for nonstationary transport equation, considered in a limited plain area of R₃, for the simultaneous determination of the pair {u, σ}.

We present the smoothness of the area under consideration, taking into account the area of the prostate, to prove the lemma 1-4, on the basis of the lemma is proved Theorem 1.

Keywords: transfer equation, local properties, the collision integral, one-speed time-dependent equation, initial condition, boundary condition, solution correctness issues, limited simple area from R3.

В настоящей статье изучаются локальные свойства интеграла столкновений односкоростного нестационарного уравнения переноса, а также классического решения нестационарного уравнения переноса излучения, рассматриваемого в простой ограниченной области из R₃.

Уравнение переноса рассмотрено при следующих предложениях [1-4]:

• все частицы имеют одинаковые по модулю скорости,
• поток частицы из вакуума на внешнюю границу отсутствует,
• индикатриса рассеяния 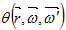  представлена в виде  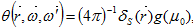где μ₀-косинус угла между направлениями .

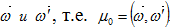При этих предложениях уравнение переноса имеет вид 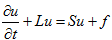  (1)

Здесь 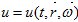- функция распределения частиц, 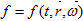- функция источника, 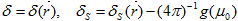- индикатриса рассеяния, 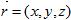- пространственные координаты, 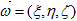- точки единичной сферы Ω со сферическими координатами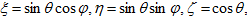

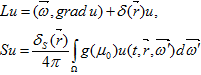
Будем говорить, что поверхность 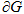 области G принадлежит классу  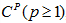если в некоторой окрестности каждой точки  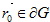она представима уравнением,  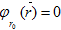причем  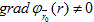и функция  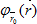непрерывна, вместе со своими производными до порядка ρ включительно в упомянутой окрестности. Поверхность  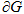называется кусочно-гладкой, если она состоит из конечного числа поверхностей класса [1-4].

Будем считать, что область G,  в которой происходит процесс переноса, состоит из конечного числа подобластей (зон) G_j ограниченных кусочно-гладкой поверхностью, 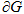_j т.е.  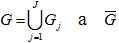 - выпуклым. Через  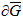обозначим внешнюю поверхность области G. Граничная поверхность  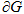области содержит кроме  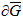еще поверхности  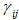раздела зон (части поверхности 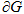_j) G_j.

Кроме того полагается, что множество 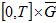 - удовлетворяет условию «обобщенной выпуклости» см. Гермогеновой [1-4]  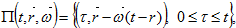являющаяся характеристикой дифференциального выражения  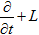и проходящая через любую точку  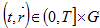при любом  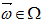имеет конечное число  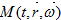точек 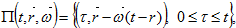 пресечений с граничной поверхностью  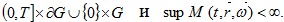 Здесь 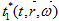 есть время пересечения характеристикой  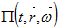границы множества .

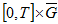Для включения в рассмотрение областей, отдельных участки поверхности которых имеют прямолинейных образующие, последние достаточно продолжить вдоль образующих по всей области, увеличив тем самым количество зон G_j [1-4].

Для однозначной разрешимости к уравнению (1) необходимо присоединить начальное распределение частиц

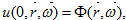   (2)

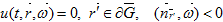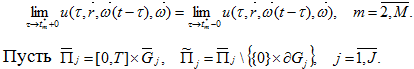и режимы на внешней границе и на границе раздела зон    (3)    (4) 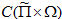 - класс функции  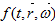непрерывных в каждом множестве  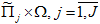и таких, что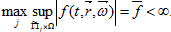

Заметим, что, если 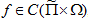 то при стремлении  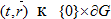вдоль различных прямых, пределы  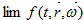существуют и вообще говоря различны.

ОПРЕДЕЛЕНИЕ 1. Классическим решением задачи (1)- (4) в области 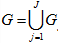 назовем функцию  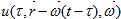которая для всех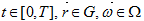 

• непрерывна по τ на отрезках 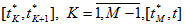 и непрерывно дифференцируема по τ в интервалах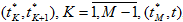 
• допускает существование интеграла столкновений 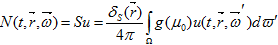 принадлежащего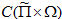 
• удовлетворяет уравнению

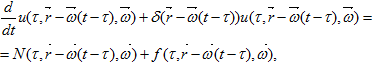  (5)

начальному условию (2) и граничным условиям (3)-(4).

Интегрируя уравнение (5) по переменной τ от 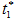 до t с учетом начального и граничных условий (2)-(4), имеем

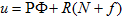  (6)

где операторы P и R определены формулами 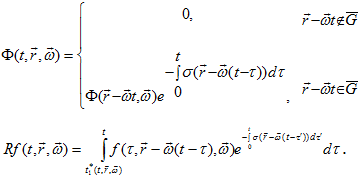Действуя на уравнение (6) оператором S, для интеграла столкновений N получаем  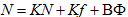 (7) 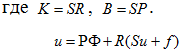   (8) Операторы  P и R определены формулами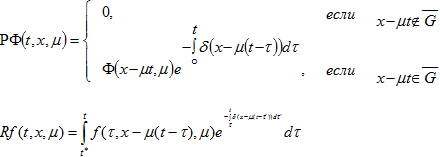

Умножим функцию 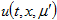, определенную формулой (8) на 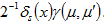. Полученное при этом уравнение проинтегрируем по переменной μ' от -1 до 1. Меняя порядок интегрирования в полученных при этом повторных интегралах приходим к уравнению

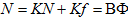  (9)

Операторы K и B определены формулами

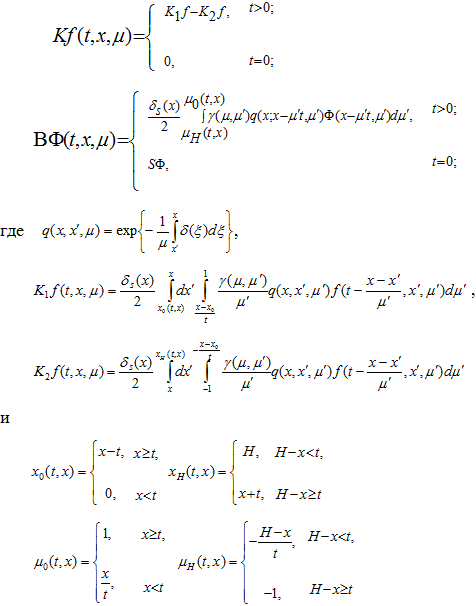
Для изучения свойств гладкости интеграла столкновений изучим свойства функций 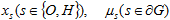 и операторов K и B.

Нам нужны следующие леммы:

Лемма  1.  I)  Для любых 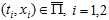 верно неравенство  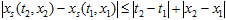 (10) a, первые производные от x_S терпят разрыв 1-ого рода лишь на линиях 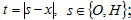II) Для любых  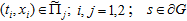верно неравенство  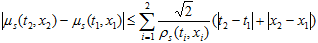  (11) где 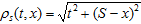, причем первые производные функций  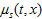терпят разрыв 1-го рода лишь на линиях .

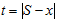Доказательство. Утверждение первого предложения, а также непрерывная дифференцируемость функций 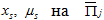, кроме линии  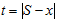непосредственно следует из определения этих функций. Докажем неравенство (11) при S=0. Положим  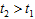и оценим разность 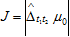. Она отлична от нуля, лишь когда 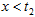. Но тогда справедливо неравенство

а потому, в силу неравенства треугольников и очевидного неравенства 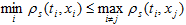   (12)

следует справедливость оценки (11) при S=0. Неравенства (11) при s=h, s=H доказываются в результате аналогичных выкладок. Лемма доказана.

Лемма 2. Пусть выполнены условия 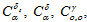 тогда оператор  действует из  .

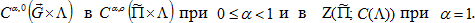Доказательство. Пусть 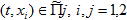. При t=0 очевидно неравенство

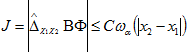
Поэтому пусть 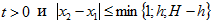. Легко видеть, что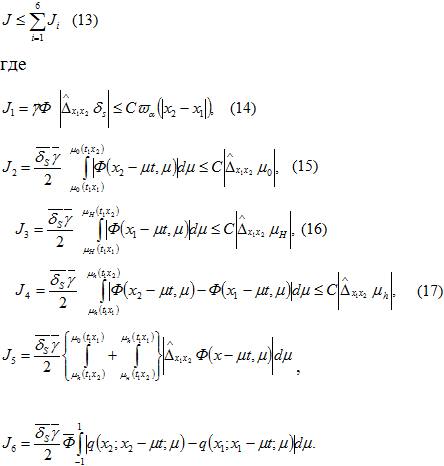

При 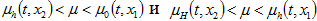 справедливы соответственно неравенства 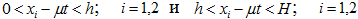. Следовательно, в силу условий леммы

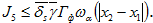  (18) Используя технику, применяемую В.И.Агошковым в [5], и неравенство  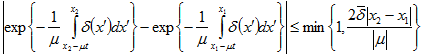 (19) справедливое  при 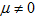, можем  оценить  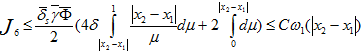  (20) Из (13) в силу неравенств (14)-(18), (20) получим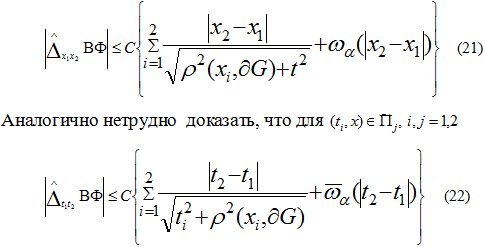

Из  соотношений (21), (22) и неравенства (12) видим, что функция  принадлежит пространству 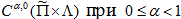 и пространству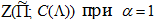 

Лемма   доказана.

Если, кроме условий леммы 2, выполнены условия согласования А, то неравенства (15) - (17) могут быть усилены. Действительно, в этом случае

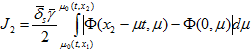
И так как при 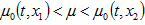 верны неравенства 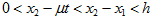,  то 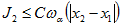   (23) Аналогично оцениваются величины J₃;   J4: 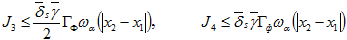Поэтому из (13) в силу неравенств (14), (23), (24), (18), (20) имеем  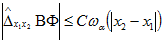 (25) Аналогично можно доказать оценку  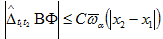  (26)

Из соотношений (25), (26) и неравенства треугольников следует справедливость следующей леммы.

Лемма 3. Если, кроме условий 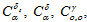  выполнены условия согласования A, то оператор Bдействует из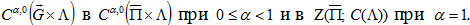

Лемма 4. Пусть выполнены условия 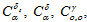 тогда оператор K переводит  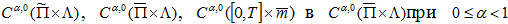и классы функций ,  в  причём справедливо неравенство

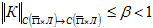  (27) Доказательство.  Пусть  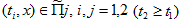Докажем справедливость оценки  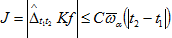 (28)

Так как при 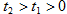 верны неравенства  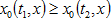и 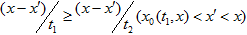, то очевидно

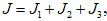  (29) где 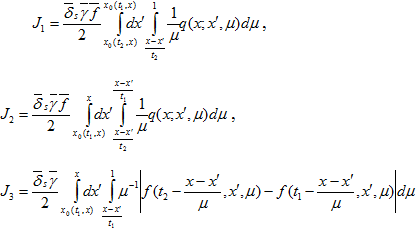Для интеграла  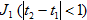справедливо неравенство  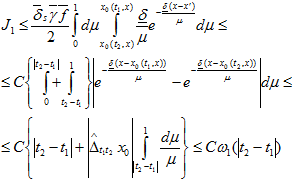 (30) Нетрудно также оценить  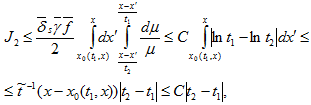 (31) где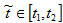  ограничены. Действительно, в силу неравенства 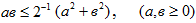и формулы 1.2.52.8 из [6] имеем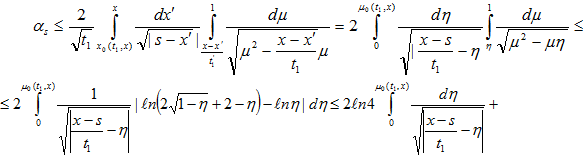 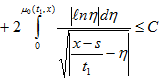  (32)

Следовательно, при 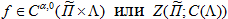  или имеем

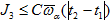   (33)

Нетрудно видеть, что оценка (33) верна и при

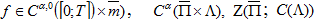
Таким образом доказали справедливость неравенства(28).

Аналогичные выкладки показывают, что справедлива оценка

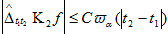
а потому верно неравенство

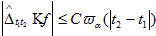      (34)

Неравенство (4.34) имеет место и при , так как в этом случае можно воспользоваться очевидным неравенством 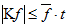Аналогично доказывается, что при  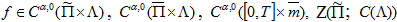 неравенство  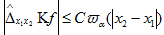     (35)

Из соотношений (34) - (35) следует, что при условиях леммы оператор K переводит 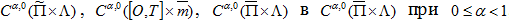, а классы функций .

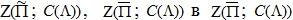Остаётся доказать неравенство (27). Без ограничения общности можем полагать, что 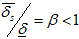, поэтому, если  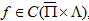то

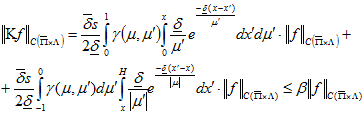
Лемма доказана.

В силу лемм 2 - 4 и используя технику доказательства теоремы 1, нетрудно видеть, что верна.

Теорема 1. Пусть выполнены условия 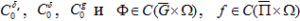, тогда существует единственное классическое решение задачи (1) –(4).

 

Список литературы / References

1. Аниконов Д.С. Об обратных задачах для уравнения переноса./ Аниконов Д.С. //Всесоюзный журнал, Дифференциальные уравнения, г.Минск, Т.10, №1, 1974, С.7-17.
2. Гермогенова Т. А. Локальные свойства решения уравнения переноса./ Гермогенова Т. А. –Москва, Наука, 1986. –272 с.
3. Сариев А.Д. Глобальная теорема об устойчивости решения обратных задач нестационарного уравнения переноса./ Сариев А.Д. // Республиканский журнал: Доклады АН РК, серия Физ-мат наук, №1, 2001г, С.16-21.
4. Султангазин У.М. Методы сферических гармоник и дискретных ординат в задачах кинетической теории переноса. / Султангазин У.М. В книге: Алма-Ата, Наука, 1979. –269 с.
5. Агошков В.И. О гладкости решений уравнения переноса и приближенных методах их построения, / Агошков В.И. В книге: Дифференциальные и интегро-дифференциальные уравнения – Новосибирск, 1977.-Выпуск- I. – С.44-58
6. Сариев А. Д. Об областях неопределённых производных высокого порядка от интеграла столкновений нестационарного уравнения переноса./ Сариев А. Д. В книге: По проблеме вычислительной математике и методы научных исследований: 2- Республиканская конференция. Алма-Ата, 1988., С. 19-22.

 Список литературы на английском языке / References in English 

1. Anikonov D.S. Ob obratnyh zadachah dlja uravnenija perenosa [On inverse problem for the transport equation]/ Anikonov D.S. //Vsesojuznyj zhurnal, Differencial'nye uravnenija, [Union journal Differential Equations].Minsk, V.10, №1, 1974, P.7-17. [in Russian]
2. Germogenova T. A. Lokal'nye svojstva reshenija uravnenija perenosa. [Local properties solving the transport equation] / Germogenova T. A. –Moskva, Nauka, 1986. –272 p. [in Russian]
3. Sariev A.D. Global'naja teorema ob ustojchivosti reshenija obratnyh zadach nestacionarnogo uravnenija perenosa.[ Global stability theorem for solving inverse problems of non-stationary transfer equation] / Sariev A.D. // Respublikanskij zhurnal: Doklady AN RK, [National Journal: Reports of the Republic of Kazakhstan] serija Fiz-mat nauk, №1, 2001g, P.16-21. [in Russian]
4. Sultangazin U.M. Metody sfericheskih garmonik i diskretnyh ordinat v zadachah kineticheskoj teorii perenosa. [Methods of spherical harmonics and discrete ordinates in problems of the kinetic theory of transport] / Sultangazin U.M. V knige: Alma-Ata, Nauka, 1979. –269 p. [in Russian]
5. Agoshkov V.I. O gladkosti reshenij uravnenija perenosa i priblizhennyh metodah ih postroenija, [The smoothness of the transfer equation and approximate methods of constructing them]/ Agoshkov V.I. V knige: Differencial'nye i integro-differencial'nye uravnenija [In: Differential and integral-differential equations] – Novosibirsk, 1977.-Vypusk- I. – P.44-58 [in Russian]
6. Sariev A. D. Ob oblastjah neopredeljonnyh proizvodnyh vysokogo porjadka ot integrala stolknovenij nestacionarnogo uravnenija perenosa. [Domains indefinite-order derivatives of the collision integral non-stationary transfer equation]/ Sariev A. D. V knige: Po probleme vychislitel'noj matematike i metody nauchnyh issledovanij: 2- Respublikanskaja konferencija. [In the book: On the issue of computational mathematics and methods of research: 2 Republican Conference], Alma-Ata, 1988, P. 19-22. [in Russian]