ФОТОГРАММЕТРИЧЕСКАЯ РЕФРАКЦИЯ В МОДЕЛИ ОДНОРОДНОЙ АТМОСФЕРЫ

Федянин М.Р.¹, Лазарев В.М.²

^1,2Кандидат технических наук,

Томский государственный архитектурно-строительный университет

ФОТОГРАММЕТРИЧЕСКАЯ РЕФРАКЦИЯ В МОДЕЛИ ОДНОРОДНОЙ АТМОСФЕРЫ

Аннотация

При выполнении геодезических измерений необходимо учитывать влияние рефракции для объектов, находящихся в пределах земной атмосферы. В работе предлагается использовать  модель атмосферы с постоянной плотностью и проводится сравнение со "Стандартная атмосфера ГОСТ 4401-73" [1, с. 1-117]. Результаты вычислений углов рефракции сравнивались с результатами численного интегрирования интеграла рефракции группы И. Г. Колчинского, приведёнными в [2, с. 34-36].  Прослеживается хорошее согласие углов фотограмметрической рефракции в наших вычислениях и в [2, с. 34-36] для всех высот вплоть до 80° по зенитному расстоянию. Рассмотрено также определение (относительных) воздушных масс.

Ключевые слова: геодезические измерения,астрономическая рефракция, фотограмметрическая рефракция, однородная атмосфера, показатель преломления, плотность воздуха, инвариантное соотношение теории рефракции, воздушная масса.

Fedyanin M.R.¹, Lazarev V.M.²

^1,2PhD in Engineering,

Tomsk state architectural and construction university

PHOTOGRAMMETRIC REFRACTION IN MODEL OF HOMOGENEOUS ATMOSPHERE

Abstract

When performing geodetic measurements one must take into account the effect of refraction for objects within the earth atmosphere. Authors propose to use the model of the atmosphere with a constant density and make a comparison with the "Standard atmosphere GOST 4401-73" [1, p.1-117]. The results of refraction angle calculations are compared with the results of numerical integration of the refraction integral of I.G. Kolchinskiy group given in [2, p.34-36]. There is a good compliance of photogrammetric refraction angles in calculations resulted and those in [2, p. 34-36] for all heights up to 80° of zenith angle. We also consider the definition of (relative) air masses.

Keywords: geodetic measurements, astronomical refraction, fotogrammetrichesky refraction, uniform atmosphere, index of refraction, air density, invariant ratio of the theory of a refraction, air mass.

При изучении астрономической и фотограмметрической рефракции обычно используется модель сферически-слоистой атмосферы, которая по физическим представлениям считается наиболее близкой к реальной атмосфере Земли. При этом поверхности равных значений плотности и соответственно коэффициента преломления будут концентрическими сферами, центр которых совпадает с центром Земли. Модель атмосферы с постоянной плотностью воздуха [3,с.94-95] считается весьма искусственной, далёкой от представлений о строении реальной атмосферы и не обещающей достаточной точности при её использовании для решения рефракционных задач.

Однако модель однородной атмосферы обладает несомненной простотой и наглядностью. После некоторого усовершенствования  она была успешно применена при создании модели несферической атмосферы Земли [4, с.3-26]. Ниже модель однородной атмосферы используется для вычисления углов астрономической и фотограмметрической рефракции в слое атмосферы ниже той точки, с которой производится фотосъёмка местности. В той или иной мере используются представления трёх моделей: сферически-слоистой, однородной по плотности и стандартной (статической) атмосферы [1, с.1-117].

Оставляя в стороне простейший случай плоской однородной атмосферы  перейдём к рассмотрению сферической атмосферы (см. рис.1). Точка В - точка, с которой производится фотосъёмка. В реальной атмосфере плотность воздуха ρ убывает с ростом высоты h над уровнем моря примерно по экспоненциальному закону. Мысленно сожмём слой атмосферы ниже точки В до слоя конечной высоты, в пределах которого плотность воздуха постоянна и равна плотности у основания слоя.  Между верхней границей этого слоя и границей слоя точки В будет существовать вакуум. Таким же образом остаток атмосферы выше точки В превратится в слой конечной высоты (толщины) с постоянной плотностью, равной плотности воздуха в точке В. Луч света, направленный из точки А местности под видимым зенитным углом Z, распространяется в однородном слое атмосферы по прямой, в точке С испытывает преломление по закону  Снеллиуса, и,  двигаясь также по прямой, попадает в точку В. Введём следующие обозначения:  φ  -  видимый надирный угол фотографирования из точки В;   r - внешний угол треугольника АВС - угол рефракции луча при его распространении от поверхности Земли до точки В;  r_А   и  r_B  - внутренние углы  ∆ АВС,    r_B   -  угол фотограмметрической рефракции, подлежащей определению в настоящей работе.  b = AO, c = CO, d = BO  - расстояния, соответственно, точек  А, С и В от центра Земли. ВО' = Н_ф - высота фотографирования над точкой О' местности.  В общем случае

                                                              b = h_A+R₃ ; с = b + H_ρ ; d = H_ф + h_O' + R₃ .                                                              (1)

В (1): h_A  и h_O'  - высоты точек А и О' соответственно над уровнем моря;  R₃ - радиус Земли; H_ρ - высота однородной по плотности атмосферы над точкой А для слоя атмосферы от уровня точки А до уровня точки В. При распространении луча за точку В угол φ' - угол преломления в остаточном однородном слое с плотностью воздуха ρ_В. Высоту однородной атмосферы H_ρ  можно представить в виде

_,                                                                                                                             (2)

здесь ρ_О - плотность воздуха на нижней границе, а интегрирование в атмосфере производится до высоты с граничным (пренебрежимо малым) значением плотности ρ_гр. Сам интеграл представляет собой массу воздуха над площадкой единичного сечения от высоты  h_о  до высоты h_гр.

В [1,с.95] приведена высота однородной атмосферы, имеющая обозначение  H_p , которая рассчитывалась по формуле

,                                                                                               (3)

где R - удельная газовая постоянная; абсолютная температура Т и ускорение свободного падения g берутся для нижней границы слоя (имеющего высоту  h_о  в обозначении формулы (2)). Формулы (2), (3) дают одинаковый

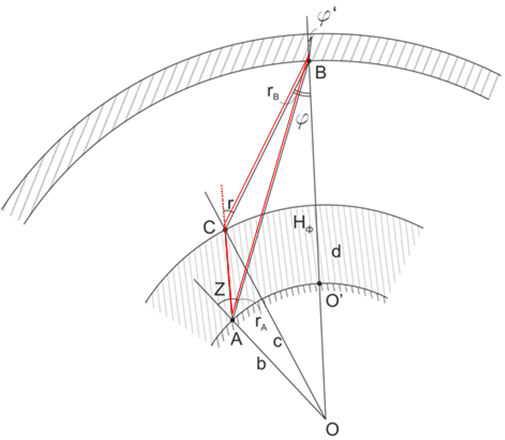
Рис. 1 – К расчету углов r, r_А  и r_B в модели атмосферы с постоянной плотностью

результат, что является одним из критериев  внутренней согласованности параметров стандартной (статической) атмосферы [1,с.1-117].

При выполнении дальнейших расчетов предполагалось, что высоты точек А и О' равны нулю, а показатель преломления определяется из выражения [5,с.21]:

                                                                                   n - 1 = 78.85P/T*10^-6.                                                                                  (4)

Для стандартных значений метеопараметров (Р = 1013.25 мбар, Т = 288.15  сухой воздух) для белого света по формуле (4) получим:  n_c  = 1.00027727.

Приводим алгоритм вычисления углов  r, r_A, и r_B .

1. Вычисление r. Угол r найдём как разность углов астрономической рефракции при распространении луча через всю толщу атмосферы и через остаток атмосферной толщи выше точки В, используя модель однородной атмосферы. Астрономическая рефракция вычисляется по формуле Кассини [6,с.3-168]. В наших обозначениях она выглядит так:

                       (5)

здесь n₀ - показатель преломления, вычисленный по метеопараметрам в точке А; входящая в "с" высота однородной атмосферы бралась из [1,с.62-90] (её можно вычислить по формуле (3)). По формуле Кассини вычислим рефракцию  r₂  для слоя атмосферы выше точки В:

,                                        (6)

здесь видимый зенитный угол предварительно должен быть определён из инвариантного соотношения теории рефракции [7, с.166] :

                                      (7)

а b' = b + H_ф ; с' = b' + , (  - высота однородной атмосферы над точкой В, определяется по [62-90,1]). n_B  определяем по формуле (4) или из соотношения

.

По (5) и (6) находим r₁ и r₂,  и  окончательно:

                                                                                                 r = r₁ - r₂                                                                                                                                                 (8)

2. Вычисление r_А. Для вычисления угла r_А  необходимо знать высоту однородной атмосферы над точкой А (для слоя атмосферы между уровнями точки А и точки В).

где  - высота однородной атмосферы для всей толщи атмосферы (для стандартных значений метеопараметров  = 8.434 км);   - высота атмосферы для части атмосферы выше точки В;  множитель   приводит эту высоту к плотности воздуха . Тогда:  n = n₀;  b = R₃; c = b + ; d = R₃ + H_ф .

Полученная ниже формула для вычисления   r_А    имеет входным аргументом надирный видимый угол φ  при точке В.  Необходимо по значению Z  найти угол  φ . Связь этих углов для однородной атмосферы выглядит так:

                                             (9)

Следует заметить, что вычислив φ по (9) и применив формулу Снеллиуса, легко получить формулу (7) для φ' , т.е. оставаясь в рамках модели однородной атмосферы получить интересующее нас значение φ', не прибегая к представлениям сферически-слоистой модели. Решая треугольники АВС, АСО и др. (см. рис.1), используя формулу Снеллиуса и сохраняя при разложении тригонометрических функций в ряд по малому параметру первые члены разложения, получим следующее выражение для числа r_А :

,                                  (10)

где ρ" = 206265, а А =  ,   B =  , C =  .

3. Вычисление r_B. Угол фотограмметрической рефракции r_B,  как внутренний угол треугольника АВС, будет равен (см. рисунок)

                                                                                                r_{B =} r - r_А .                                                                                            (11)

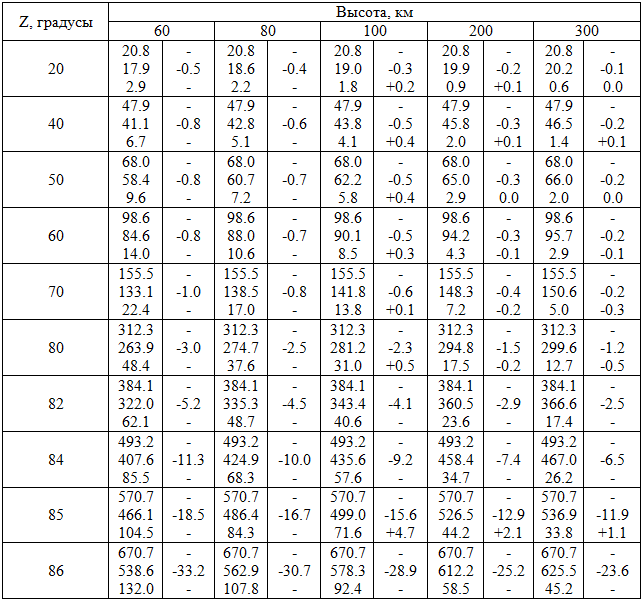
Результат вычислений по формулам (5) - (11) для различных H_ф  и  Z представлены в таблицах 1, 2.

Замечание к таблицам 1, 2. В некоторых случаях равенство    r ₌ r_А - r_В  выполняется приближенно, вследствие того, что значения  r_В  вычислялись по значениям  r  и  r_А с большим числом значащих цифр, а затем все величины округлялись до  0.1 секунды дуги. В таблицах 1, 2 приведены также результаты сравнения "наши значения - Колчинский". Группа  И. Г. Колчинского проводила вычисления  r , r_А и r_В  путём численного интегрирования  на ЭВМ с использованием Стандартной атмосферы  ВСА-60 [2, с.35]. При интегрировании атмосфера разбивалась на слои толщиной в  0.5 км.

Сравнение наших вычислений с результатами вычислений группы И. Г. Колчинского показывает, что наблюдается хорошее согласие угла  r_В  для всех высот и зенитных расстояний  Z вплоть до 80°. При аэрофотосъёмке, даже при использовании короткофокусных (широкоугольных) топографических аэрофотоаппаратов  (АФА), угол поля зрения  2φ не превышает 140°, т.е.  φ (или примерно равный ему угол Z)  70°.

Не представляет особой сложности вычисление углов рефракции в рамках однородной модели атмосферы и для других значений метео параметров (если они известны), отличных от стандартных. Описанный выше алгоритм вычисления фотограмметрической рефракции пригоден и для малых высот (съёмка с беспилотных летательных аппаратов - БПЛА),   и при

До сих дполагалось, что показатель преломления   в процессе распространения луча  остаётся неизменным. Это справедливо для монохроматического излучения.

Таблица 1 – Значения углов r, r_a  r_b в секундах дуги и разности «наши значения – Колчинский [2]»

(первая, вторая и третья строки для каждого Z соответственно)

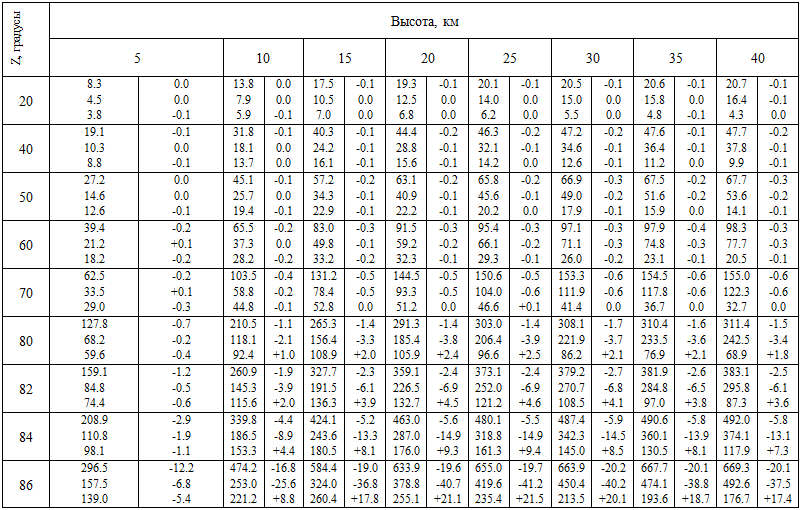
Таблица 2 – Продолжение таблицы 1 для средних и больших высот

В действительности же мы при проведении аэрофотосъёмочных работ в пределах атмосферы, и для больших высот за пределами основной толщи атмосферы (спутниковая рефракция).фотографических, визуальных и др. видах измерений, с фильтрами или без фильтров, имеем дело с гетерохромным излучением, т.е. излучением, ограниченным некоторым интервалом длин волн. С ростом воздушной массы на пути луча роль коротковолновой части в общем потоке излучения будет быстро уменьшаться (особенно на больших Z, т.е. при больших воздушных массах), и световой поток будет становиться как бы всё более и более "красным", поскольку экстинкция в коротковолновой области существенно больше, чем в длинноволновой [8, с.387-388]. Изменение эффективной длины волны  в общем потоке излучения приводит к непрерывному изменению n,  так что траектория луча, при прочих равных условиях, будет иной, по сравнению с той, которую она бы имела  при неизменном показателе преломления. Этот эффект приведёт к изменению углов рефракции, однако эти изменения незначительны, более или менее заметны при больших  H_ф  и Z.

Анализируя изменения кривой распределения энергии в спектре Солнца в зависимости от Z, можно принять, что при H_ф  = 25 км и Z = 84°  показатель преломления может изменить своё значение от  n₀    до  n = 1.000275. Тогда, сделав расчеты,  используя модель однородной атмосферы, получим следующие результаты:

r =  476.1 "; r_А  = 316.1";  r_B = 160.0".

Сравнивая эти значения с приведёнными в таблице 1, видим, что  r_B  уменьшилось на 1.3" .

В заключение следует отметить, что в модели атмосферы с постоянной плотностью легко определить (относительную) воздушную массу, широко применяемую в исследованиях по фотометрии. Её можно определить как для слоя конечной толщины, так и для всей атмосферы.

На рисунке 1: АС - длина пути луча в слое однородной атмосферы. Решая ∆АСО (используя теорему синусов), найдём АС . Относительная воздушная масса, т.е. длина пути луча в единицах высоты однородной атмосферы, есть:   М = АС/  . Приведём для сравнения небольшую таблицу 3, где приведены  М, вычисленные нами, и табличные значения по [9, с.182], для всей толщи атмосферы для пяти зенитных расстояний.

Таблица 3 – Вычисленные и табличные значения воздушных масс в функции Z.

Воздушные массы	Видимое зенитное расстояние
	50°	60°	70°	80°	90°
	1.554	1.996	2.909	5.64	38.88
	1.553	1.995	2.904	5.60	38

Список литературы / References

1. ГОСТ 4401-73. Стандартная атмосфера. Параметры. – М.: − 117с.
2. Колчинский И. Г. Рефракция света в земной атмосфере/И.Г. Колчинский. − Киев: Наукова Думка, 1967. − 44с.
3. Мак-Картни Э. Оптика атмосферы/Э. Мак-Картни.− М.: Мир, 1979. − 421с.
4. Федянин М. Р. Обоснование и разработка модели несферической атмосферы для повышения точности астрономо-геодезических измерений: Автореф. дис. на соиск. учен. степ. канд. техн. наук (25.00.32)/Михаил Романович Федянин; Сибирская государственная геодезическая академия − Новосибирск, 2003. − 26с.
5. Островский А. Л. Учет атмосферных влияний на астрономо-геодезические измерения/ А.Л. Островский, Б.М. Джуман, Ф.Д. Заблоцкий и др.− М.: Недра, 1990. − 235с.
6. Нефедьева А. И. Астрономическая рефракция. Часть первая/А.И. Нефедьева // Известия АОЭ.-1968.-№36.-с. 3-168.
7. Халхунов В. З. Сферическая астрономия/В.З. Халхунов.−М.: Недра, 1972. − 304с.
8. Курс астрофизики и звёздной астрономии, т. I/ под ред. акад. А. А. Михайлова. − М.: Наука, 1973. − 608с.
9. Аллен К. У. Астрофизические величины/К.У.Аллен.− М.: Мир, 1977. − 446с.

Список литературы на английском языке / References in English

1. GOST 4401-73. Standartnaya atmosfera. Parametry. [Standard atmosphere. Options.]- M.: 1974. – 117p. [in Russian]
2. Kolchinskii I. G. Refrakciya sveta v zemnoi atmosfere[The refraction of light in the earth's atmosphere.]/I.G. Kolchinskii. - Kiev: Naukova Dumka, 1967. – 44 p. [in Russian]
3. Mak-Kartni E. Optika atmosfery[Atmospheric Optics.]/E. Mak-Kartni.- M.: Mir, 1979. – 421 p. [in Russian]
4. Fedyanin M. R. Obosnovanie i razrabotka modeli nesfericheskoi atmosfery dlya povysheniya tochnosti astronomo-geodezicheskih izmerenii. [Justification and development of a non-spherical model of the atmosphere to increase the accuracy of astronomical and geodetic measurements]: Avtoref. dis. na soisk. uchen. step. kand. tehn. nauk (25.00.32) [Abstract of dissertation for the degree of candidate of technical sciences. (25.00.32)] /Mihail Romanovich Fedyanin; Siberian State Academy of Geodesy- Novosibirsk, 2003. – 26 p. [in Russian]
5. Ostrovskii A. L. Uchet atmosfernyh vliyanii na astronomo-geodezicheskie izmereniya.[ Accounting for atmospheric effects on astronomical and geodetic measurements.]/ A.L. Ostrovskii, B.M. Dzhuman, F.D. Zablockii and others.- M.: Nedra, 1990. – 235 p. [in Russian]
6. Nefed'eva A. I. Astronomicheskaya refrakciya. Chast' pervaya [Astronomical refraction. Part one]/A.I. Nefed'eva // News AOE.-1968.-№36.-p. 3-168. [in Russian]
7. Halhunov V. Z. Sfericheskaya astronomiya[Spherical astronomy.]/V.Z. Halhunov.-M.: Nedra, 1972. – 304 p. [in Russian]
8. Kurs astrofiziki i zvezdnoi astronomii, t. I[Course of astrophysics and stellar astronomy, vol. I] / pod red. akad. A. A. Mihailova [edited by acad. A.A. Mixailova.]. - M.: Nauka, 1973. – 608 p. [in Russian]
9. Allen K. U. Astrofizicheskie velichiny[Astrophysical quantities.]/K.U.Allen.- M.: Mir, 1977. – 446 p. [in Russian]