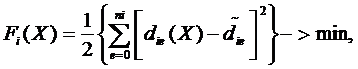ПРИМЕНЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В МОДЕЛИРОВАНИИ САУ РЕАЛЬНЫМИ ОБЪЕКТАМИ
Прохорова О.В.1, Неклюдов С.В.2
1 Доктор технических наук, доцент, 2 студент, Самарский государственный архитектурно-строительный университет
ПРИМЕНЕНИЕ ЗАДАЧ НЕЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ В МОДЕЛИРОВАНИИ САУ РЕАЛЬНЫМИ ОБЪЕКТАМИ
Аннотация
В статье рассмотрено применение задачи нелинейного программирования на этапе оптимизации целевой функции системы автоматического управления (САУ) градиентным методом, написана программа для ее решения. Решение было применено для проектирования САУ химическим реактором.
Ключевые слова: автоматизация, оптимизация, градиентный метод, JAVA.
Prokhorova O.V.1, Neklydov S.V.2
1 PhD in Engineering, Associate professor, 2 student, Samara State University of Architecture and Civil Engineering
PROBLEM OF APPLYING NONLINEAR PROGRAMMING IN MODELING ACS OF REAL OBJECTS
Abstract
The article considers problem of applying nonlinear programming on step of optimization objective function of automatic control system (ACS) by the gradient method, program was written to solve it. The solution was applied to design the ACS of the chemical reactor.
Keywords: automation, optimization, the gradient method, JAVA
В современном производстве часто возникают задачи синтеза систем автоматического управления (САУ) сложными объектами. Одним из этапов моделирования таких систем является оптимизации целевой функции, которая, как правило, нелинейная. Чтобы упростить данный этап моделирования, используют специализированные программы.
Существуют различные алгоритмы оптимизации:
- Метод Ньютона – Раффсона;
- Метод дихотомии;
- Метод Фибоначчи и др.
Авторами разработан алгоритм моделирования САУ химическим реактором, включающий реализацию задачи поиска оптимальных значений настраиваемых параметров регулятора. Для этого был разработан код решения системы нелинейных алгебраических уравнений методом градиентного спуска с дроблением шага. Оптимизация на основе градиентного метода позволила найти оптимальные значения варьируемых параметров САУ, при которых соблюдается требуемое качество управления реактором. В основу оптимизации было положено приравнивание к нулю частных производных целевой функции по параметрам. В качестве целевой функции безусловной оптимизации использовалась среднеквадратичная ошибка аппроксимации [1]:
где 
- коэффициенты характеристического уравнения САУ, представленные функциями варьируемых параметров Х,
- коэффициенты эталонного характеристического уравнения, задаваемого в соответствии с заданными требованиями, предъявляемыми к качеству САУ.
Метод градиентного спуска основан на свойстве градиента функции, согласно которому направление градиента совпадает с направлением наискорейшего возрастания функции, а направление антиградиента – с направлением наискорейшего убывания функции. Решение начинается с задания начальной точки 
- начальных значений вектора варьируемых параметров. Последующие точки находятся согласно формуле:
,
где 
- значение вектора-градиента целевой функции на предыдущем шаге, 
- значение шага на итерации. Для выбора значения шага была использована процедура дробления шага, где на каждой итерации проверялось, уменьшение модуля вектора-градиента. Если модуль вектора-градиента не уменьшился, то величина шага делилась пополам, и итерация повторялась заново.
В качестве объекта управления (ОУ) был выбран химический реактор. А в качестве моделируемой системы была выбрана схема САУ+ ОУ. При этом соблюдалось правило управления объектом по непрерывной схеме, где на каждом участке было необходимо контролировать несколько физических и технических параметров, влияющих на качество получаемого продукта. К проектируемой САУ предъявлялись жесткие требования – стабильность, запас устойчивости, допустимая колебательность во время переходного процесса.
Задача синтеза САУ химическим реактором [2] решалась на основе метода моделирования процессов в комплексной плоскости, описанного одним из авторов в работе [1]. Для дальнейшего продвижения данного направления моделирования и синтеза САУ реальными объектами и процессами, была решена задача оптимизации целевой функции градиентным методом, описанным выше, с использованием разработанного кода на языке программирования Java, который состоит из двух классов и представлен ниже.
public class GradientMethod {
public static void main(String[] args) throws IOException {
double g = 1; // постоянная шага
double e = 0.0001; //точность
double l = 0.3; //коэффициент дробления
double[] variables = new double[30];
double[] grads = new double[30];
double gradM;
int k = 1, kmax = 100, m = 0;
BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
System.out.println("Enter count of variables:");
int n = 0;
try {
n = Integer.parseInt(reader.readLine());
} catch (IOException e1) {
System.out.println("Wrong number");
}
for (int i = 0; i < n; i++){
System.out.println("Enter the initial value of variable:");
variables[i] = Double.parseDouble(reader.readLine());
grads[i] = DerivativeOfFunctionAndFunction.getValueOfDerivative(variables, i);
}
while (k < kmax){
double[] new_variables = new double[30];
for (int i = 0; i < n; i++) {
new_variables[i] = variables[i] - g * grads[i];
System.out.println(new_variables[i]);
}
double func1 = DerivativeOfFunctionAndFunction.getValueOfFunction(variables);
double func2 = DerivativeOfFunctionAndFunction.getValueOfFunction(new_variables);
if (func2 < func1){
variables = new_variables;
for (int i = 0; i < n; i++)
grads[i] = DerivativeOfFunctionAndFunction.getValueOfDerivative(variables, i);
gradM = getModuleOfGradient(grads, n);
if (gradM <= e)
break;
k = k + 1;
} else {
if (m >= 50) {
for (int i = 0; i < n; i++){
System.out.println("X" + (i+1) + " = " + String.format("%.4f",variables[i]));
}
System.out.println("F(*) = " + DerivativeOfFunctionAndFunction.getValueOfFunction(variables));
System.out.println("Continue calculating? (y/n)");
String str = reader.readLine();
if (!str.equals("y"))
break;
m = 0;
}
m++;
g = g * l;
}
}
for (int i = 0; i < n; i++){
System.out.println("X" + (i+1) + " = " + String.format("%.4f",variables[i]));
}
System.out.println("F(*) = " + DerivativeOfFunctionAndFunction.getValueOfFunction(variables));
}
private static double getModuleOfGradient(double[] grads, int n){
double module = 0;
for (int i = 0; i < n; i++) {
module = module + Math.pow(grads[i], 2);
}
return Math.sqrt(module);
}
}
public class DerivativeOfFunctionAndFunction {
static double getValueOfDerivative(double[] x, int i){
double[] f = new double[30];
/*Write partial derivatives of your function*/
f[0] = 2*(x[0]-0);
f[1] = 2*(x[1]-9/4);
return f[i];
}
static double getValueOfFunction(double[] x){
double f;
/*Write your function*/
f = (x[0]-0)*(x[0]-0) + (x[1]-9/4)*(x[1]-9/4);
return f;
}
}
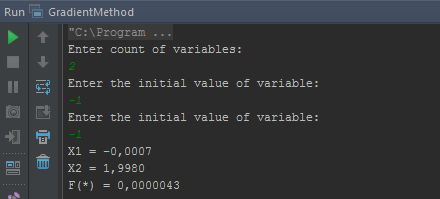
Рис. 1. Работа программы оптимизации
Литература
- Прохорова О.В. Оптимизация и синтез многомерных САУ на основе моделирования процессов в s-области. Монография. Москва: АПКиППРО, 2010. - 158 с.
- Рей У. Методы управления технологическими процессами.- М.: Мир, 1983.- 365 с.
References
- Prohorova O.V. Optimizacija i sintez mnogomernyh SAU na osnove modelirovanija processov v s-oblasti. Monografija. Moskva: APKiPPRO, 2010. - 158 s.
- Rej U. Metody upravlenija tehnologicheskimi processami.- M.: Mir, 1983.- 365 s.