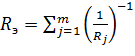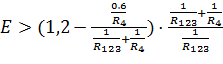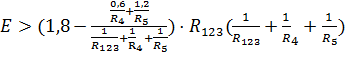АЛГОРИТМ МОДЕЛИРОВАНИЯ ДИОДНО-РЕЗИСТИВНЫХ СХЕМ

Мыльников А.И.¹, Новиков В.В.²

¹ ORCID: 0000-0002-9573-5530, студент, Университет ИТМО (Санкт-Петербург), ² ORCID: 0000-0001-5317-2103, аспирант, Университет ИТМО

АЛГОРИТМ МОДЕЛИРОВАНИЯ ДИОДНО-РЕЗИСТИВНЫХ СХЕМ

Аннотация

В статье описывается алгоритм компьютерного моделирования диодно-резистивных схем на базе метода узловых потенциалов с использованием ступенчатой аппроксимации вольт-амперной характеристики диода. Алгоритм создан в рамках разработки визуального обучающего конструктора схем. Представлен пример моделирования диодно-резистивной схемы с применением разработанного алгоритма.

Ключевые слова:  электрические схемы, компьютерное моделирование, модель диода, ступенчатая аппроксимация ВАХ

Myl'nikov A.I.¹, Novikov V.V.²

¹ ORCID: 0000-0002-9573-5530, student, ITMO University (Russia, Saint-Petersburg), ² ORCID: 0000-0001-5317-2103, postgraduate student, ITMO University

THE SIMULATION ALGORITHM OF DIODE-RESISTIVE CIRCUITS

Abstract

The article describes the algorithm of simulating diode-resistive circuits with piecewise-defined approximation current-voltage characteristics of diode. This algorithm was made for visual electric scheme constructor. An example of modelling scheme with using described algorithm is shown.

Keywords: electric schemes, computer simulation, diode modelling, piecewise-defined approximation of I-V curve

ВВЕДЕНИЕ

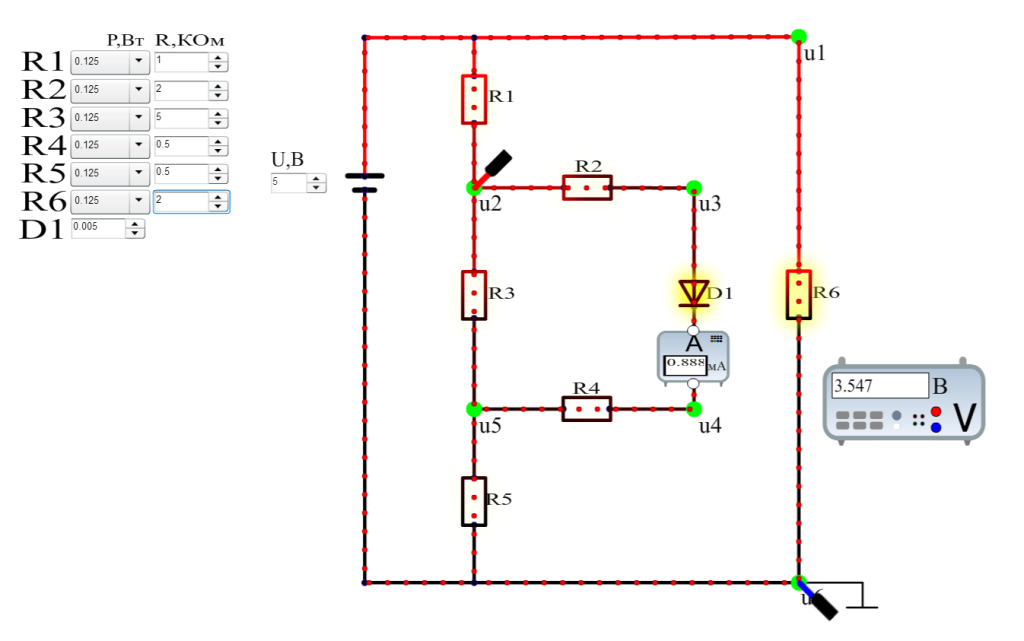
На протяжении нескольких учебных семестров в университете ИТМО на факультете СПО успешно применяются методы компьютерного моделирования для обучения студентов фундаментальным основам работы вычислительной техники. В частности, в курсе «Основы электронной обработки информации», применяются так называемые визуальные модели [1-7], задача которых заключается в демонстрации и скрытых или неочевидных процессов в изучаемом объекте/явлении. Разработанные методы визуализации электрических процессов в цепях [6,7], показали свою состоятельность в рамках проведенных педагогических экспериментов, а соответствующие визуальные модели резистивных и диодно-резистивных цепей (рисунок 1) были успешно внедрены в учебный процесс факультета.

Рисунок 1 – пример визуальной модели

Однако главным недостатком существующих визуальных моделей является их «статичность» или неизменяемость структуры схемы электрического устройства, в связи с чем, некоторые эффекты резистивных и диодно-резистивных цепей не могут быть продемонстрированы достаточно ясно. Одним из путей устранения этого недостатка – добиться полной интерактивности при создании схем на уровне составных элементов, т.е. фактически перейти от статичных визуальных моделей к визуальному конструктору схем.

В то же время визуальные модели (в рамках курса «основы электронной обработки информации») строились на базе ступенчатой аппроксимации вольт-амперных характеристик полупроводникового диода [1-5, 7], что означает необходимость разработки специального алгоритма моделирования диодно-резистивных цепей с учетом этой аппроксимации. Далее в статье представлено обоснование алгоритма моделирования диодно-резистивной цепей и приведен пример его применения.

1. Аппроксимация вольт-амперной характеристики полупроводникового диода

Как отмечалось в работах [1-5], специфика моделирования диодно-резистивных цепей обуславливалась двумя факторами: во-первых, в рамках вышеупомянутого курса «Основы электронной обработки информации» рассмотрению подлежат вопросы функционирования электронных устройств на цифровом уровне, и, следовательно, интерес представляют их цифровые режимы работы; во-вторых, образовательный уровень студентов накладывает ограничение на сложность применяемых в курсе математических моделей полупроводниковых приборов.

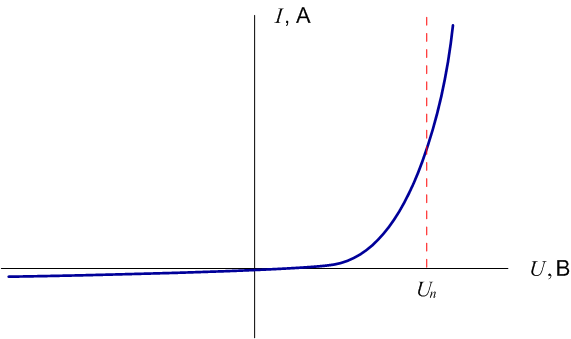
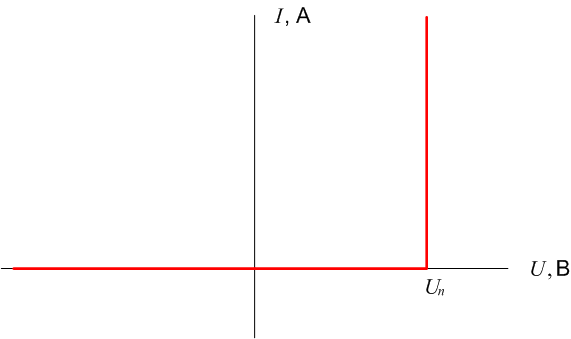
Учитывая эти факторы, в прежних работах было предложено использование ступенчатой аппроксимации вольт-амперной характеристики (ВАХ) полупроводникового p-n перехода (рисунок 1 а,б), которая позволяет моделировать электронные устройства в цифровых режимах с приемлемой для студентов сложностью математической модели (1.1).

а	б

Рисунок 2: а – принципиальная ВАХ диода, б – аппроксимированная ВАХ

                                                                                             (1.1)

Таким образом диод можно рассматривать как электрический элемент, который может находиться в двух состояниях: закрытом (I = 0 А) и открытом (I > 0 А). В качестве пороговой величины перехода в открытое состояние используются значение U_п = 0,6 В, которое соответствует типам полупроводниковых диодов применяемых в цифровой технике.

• Алгоритм моделирования диодно-резистивных цепей

Как известно, с точки зрения математической формализации линейные (резистивные) электрические схемы могут быть описаны системой линейных уравнений, представленных в матричном виде. Применение такого подхода используется в методе узловых потенциалов, где каждое уравнение системы представляется формулой (2.1).

                                (2.1)

где:

 – рассматриваемый узел;

 – проводимость на i-ом резисторе;

 – потенциал на i-ом узле;

 – напряжение на i-ом ЭДС;

 – сила тока на i-ом источнике тока.

После решения такой системы уравнений в матричном виде получаются значения потенциалов узлов схемы.

С использованием классического метода узловых потенциалов невозможно произвести моделирование реальных электрических приборов, однако, при решении этой задачи используются схемы их замещения. Моделирование диода со ступенчатой вольт-амперной характеристикой возможно путем его замещения в схеме источником напряжения U_п = 0,6 В при открытом состоянии, и сопротивлением бесконечной величины – при закрытом.

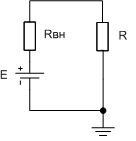
Моделирование схем предполагает использование как реальных источников напряжений и токов, так и идеальных. Для перехода к идеальным источникам их внутреннее сопротивление необходимо выбрать такое, чтобы результаты расчета не изменялись значимо, т.е. оставались в пределах заданной точности вычислений. Внутренне сопротивление источника напряжения для эквивалентной схемы (рисунок 3) может быть выбрано исходя из условия (2.2).

Рисунок 3 – схема с внутренним сопротивлением источника

,                                                                              (2.2)

где:  – сила тока в схеме при использовании идеального источника напряжения;  – сила тока при использовании реального источника напряжения;  – допустимое отклонение точности вычислений.

Выражая силы токов как (2.3) и (2.4),

                                                                                              (2.3)

                                                                              (2.4)

формула (2.2) приводится к виду (2.5), а затем к (2.6).

                                                                        (2.5)

                                                                            (2.6)

Сопротивление R эквивалентной замкнутой цепи будет наименьшим в том случае, когда все резисторы в ней соединены параллельно (2.7), и, в таком случае, для упрощения алгоритма определения внутреннего сопротивления можно использовать оценку, представленную в формуле (2.8).

                                                         (2.7)

,                                                                       (2.8)

где n – количество резисторов моделируемой замкнутой цепи.

Исходя из бинарности состояний диода с применением ступенчатой аппроксимации ВАХ, диодно-резистивные схемы максимально могут иметь  состояний диодов, где n  – количество диодов. Тогда состояние схемы описывается вектором состояния st вида (2.9).

,                                                         (2.9)

где m - количество диодов в схеме,  – состояние i-го диода в схеме: «0» – закрыт, «1» – открыт.

Идея алгоритма моделирования диодно-резистивных схемы заключается в «поиске» такого вектора состояний st для заданных параметров схемы, при котором: а) для каждого диода выполняется условие (1.1); б) возможно применение метода узловых потенциалов.

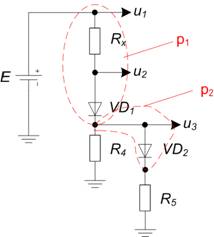
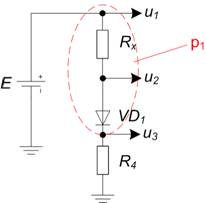
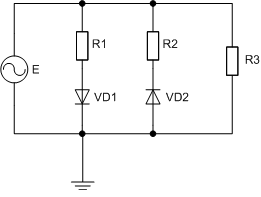
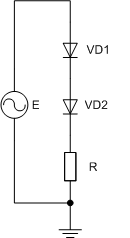
Простой перебор значений вектора st представляется мало эффективным, т.к. не учитывает взаимное влияние состояний диодов друг на друга, что существенно сокращает количество состояний схемы. Так, например, в схеме, представленной на рисунке 2а, не существует условия, при котором будут одновременно открыты диоды VD1 и VD2, а на рисунке 2б диод VD2 не может быть открыт при закрытом VD1.

а	б

Рисунок 4 – примеры диодно-резистивных цепей

Следовательно, необходимо учесть в алгоритме взаимосвязь состояний диодов между собой.

Для возможности реализации анализа схемы в алгоритме, необходима ее формализация, в качестве которой эффективно использовать графовые структуры: вершины обозначают узлы электрической схемы, дуги – соединения между ними, направление дуги совпадает с направлением включения электрического элемента в схеме. В последствии, граф электрической схемы можно преобразовать в матричный вид и применить метод узловых потенциалов.

Ниже представлено описание основных шагов алгоритма:

1. Построение графа G электрической схемы.

Вершинами будут являться электрические узлы характеризующиеся величиной потенциала, а дугами – ветви прилегающие к потенциалу. Дуги графа характеризуются тройкой (t; R; U), где: t – тип электрического элемента (0 – резистор, 1 – диод, 2 – источник напряжения); R – сопротивление элемента (для диода условно принимается ∞); U – напряжение между вершинами ветви (для t = 0 и t = 1 равняется нулю).

2. Построение графа  эквивалентной схемы.

На этом шаге алгоритма производится замена резистивных цепей исходной схемы к эквивалентным:

2.1. Для каждой цепи i графа G, все смежные вершины которой образуют ветвь j с  = 0, формируется новая дуга k графа G’, которая характеризуется парой (;; 0), а = 0, а  определяется формулой (2.10).

,                                                                         (2.10)

где n - количество дуг цепи i.

Таким образом обеспечивается замена последовательно соединенных резисторов в схеме эквивалентным.

2.2. Для всех двух v,w смежных вершин графа G’, имеющих более одной дуги и t = 0 формируется новая дуга графа , которая характеризуется тройкой (t; ; 0), где  определяется формулой (2.11).

,                                                                  (2.11)

где m – количество дуг между вершинами v,w.

На этом шаге обеспечивается замена параллельно соединенных резисторов в схеме эквивалентным.

Из двух представленных выше преобразований графа G следует, что получившийся граф  не может содержать более одной «резистивной дуги» между любыми двумя смежными вершинами.

3. Поиск состояний диодно-резистивной схемы.

3.1. Инициализация вектора состояний st (2.12):

,                                                                 (2.12)

где i – ветвь графа G.

3.2. Формирование множества цепей P графа  с элементами p, для которых степени начальных и конечной вершины больше двух.

3.3. Для каждой цепи p множества P, такой, что выполняется условие (2.13) (т.е. образующих диодно-резистивную цепь) – проверка возможности удаления такого пути из графа , моделируя тем самым состояние закрытых диодов.

,                                                                        (2.13)

где i – ветвь цепи p.

Цепь p может быть удалена, если путь тока в полученной схеме существует и замкнут.

3.4. Удаленная из графа цепь записывается в стек S, для всех диодов ветвей i из условия (2.13) устанавливается значение  = 0.

3.5. В случае, если в графе  все диодные ветви оказались в закрытом состоянии (т.е. получена резистивная схема), то осуществляется ее расчет методом узловых потенциалов и переход к пункту 3.8.

3.6. В случае, если граф  состоит из диодно-резистивной цепи j, то проверяется возможность ее открытия: напряжение цепи  должно удовлетворять условию (2.14).

,                                                                            (2.14)

где  – количество диодов в цепи j.

3.7. В случае выполнения условия (2.14), диод/диоды цепи j исходного графа электрической схемы G заменяются на источники напряжения , а их состояния принимают значения «1» – (2.15).

                                           (2.15)

В случае, если условие (2.14) не выполняется – пропустить ветвь.

3.8. Применение метода узловых потенциалов для графа G.

3.9. Пока стек S не пуст, выбрать очередную цепь j из S и перейти к пункту 3.7.

3. Пример моделирования диодно-резистивной схем на основе алгоритма

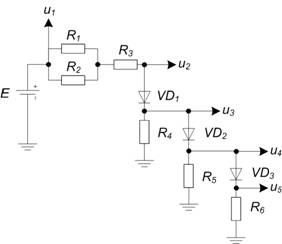
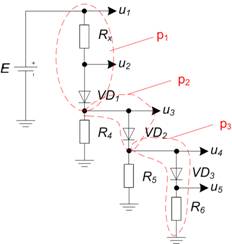
Ниже представлен пример моделирования диодно-резистивной схемы с тремя диодами (рисунок 3) на основе разработанного алгоритма. Пример демонстрирует переходы между состояниями схемы с указанием соответствующих значений входного напряжения. Результаты моделирования сопоставляются с математической моделью схемы  составленной вручную с использованием ступенчатой аппроксимации ВАХ диода. Точка перехода диода  составляет 0,6 В.

Рисунок 5 – схема примера

Математическая модель

Математическая модель схемы основана на четырех состояниях образуемых диодами. В формулах (3.1) – (3.3) представлены условия открытия диодов VD₁, VD₂ и VD₃ соответственно.

                                                                                  (3.1)

                                                (3.2)

                       (3.3)

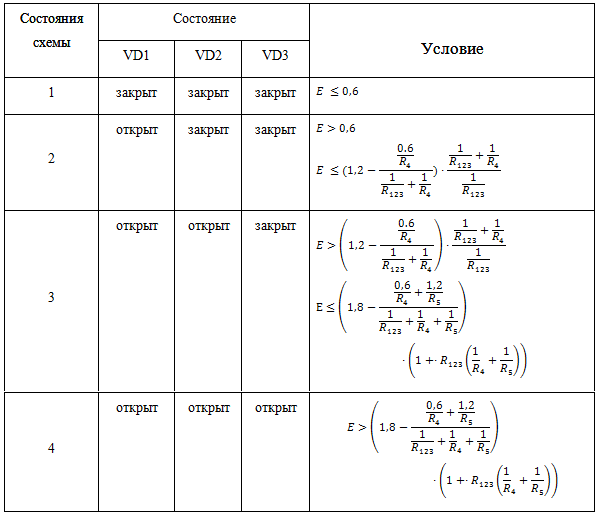
Состояния схемы и их условия представлены в таблице 3.4.

Таблица 3.4 - состояния схемы

Итеративный алгоритм извлечения диодных цепей

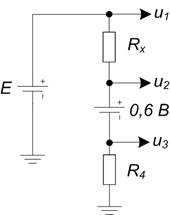
В первых шагах алгоритма производится замена исходной схемы эквивалентной (рисунок 4).

Рисунок 6 – эквивалентная схема

После чего вектор состояний st = (st₁, st₂, st₃) инициализируется единицами (диоды открыты), где st_i – состояние диода i в схеме. Затем производится поиск множества P диодно-резистивных цепей p_i в соответствии с условием (2.13).

На следующем этапе производится поиск вектора st путем определения состояния диодов. На первом шаге из схемы удаляется цепь p₃ (диод VD₃), т.к. только ее удаление обеспечивает замкнутость пути протекания тока (рисунок 5). Цепь p₃ добавляется в стек S; st = (1,1,0).

Рисунок 7 – первая итерация поиска вектора состояния st

Аналогичным образом удаляется из схемы и добавляется в стек цепь p₂ (диод VD₂) – рисунок 6.

Рисунок 6 – вторая итерация поиска вектора состояния st

Схема на рисунке 6 представляет собой диодно-резистивную цепь, и по условию (2.14) для открытия диода в ней необходимо напряжение E > 0,6 В. После  открытия диода VD₁ и расчета эквивалентной схемы (рисунок 7), проверяется условие открытия VD₂ для извлеченной из стека цепи p₂, т.е. напряжение u₃ должно быть больше 0,6 В.

Рисунок 8 – эквивалентная схема диодно-резистивной цепи

После открытия VD₂ аналогично проверяется VD₃: для открытия диода в цепи p₃ извлеченной из стека, напряжение u₄ > 0,6 В. В случае невыполнения условий соответствующая ветвь не включается в схему и производится переход к следующей цепи p_i в стеке S.

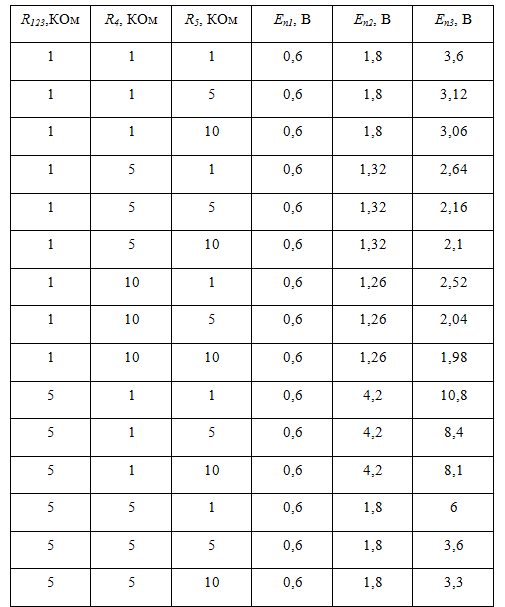
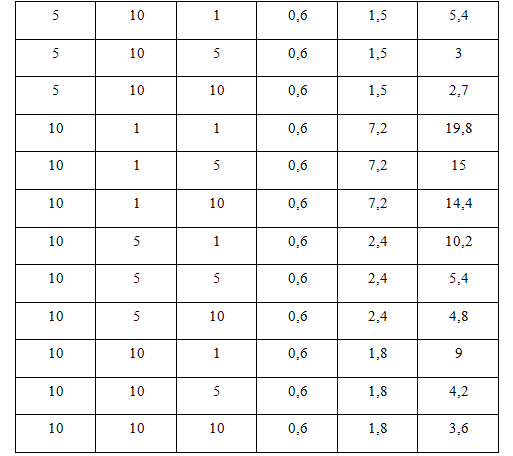
Результаты численных расчетов схемы с применением алгоритма и математической модели показывают одинаковые результаты. Использовался источник переменного напряжения, значения которого меняются линейно, с шагом dE = 0,001 В. Отклонения точности моделирования  не должны превышать 0,001. По результатам моделирования были получены значения точки перехода  (таблица 3.1) между состояниями схемы i, которые полностью совпали теоретически рассчитанными (с учетом заданной точности).

Таблица 3.1 – результаты численных расчетов с применением алгоритма

ЗАКЛЮЧЕНИЕ

Был разработан и формализован алгоритм моделирования диодно-резистивных цепей с использованием аппроксимации вольт-амперной характеристики. Результаты численных расчетов некоторых диодно-резистивных схем с применением алгоритма соответствуют их математическим моделям с учетом заданной точности.

В ближайшем времени планируется реализовать алгоритм программно, с целью поиска его ограничений и возможных нетривиальных задач. Полученные результаты войдут в состав визуального конструктора схем.

Литература

1. Новиков В.В. Виртуальный лабораторный комплекс по основам полупроводниковой цифровой электроники // Научно-технический вестник СПбГУ ИТМО. – 2008. – Вып. 52. – С. 129–133.
2. Гриншпун Д.М. Виртуальные лабораторные комплексы по основам цифровой электроники // Труды XVII Всероссийской научно-методической конференции «Телематика'2010». – СПб, 2010. – Т. 2. – С. 340–342.
3. Гриншпун Д.М. Виртуальные лабораторные комплексы по основам цифровой электронной обработки информации как средство повышения качества IT-образования // Сборник трудов IV Международной научной конференции «Современные достижения в науке и образовании». – Будва, 2010. – С. 12.
4. Новиков В.В., Гриншпун Д.М. Интерактивный визуально-демонстрационный виртуальный лабораторный комплекс по основам цифровой электроники // Труды XVII Всероссийской научно-методической конференции «Телематика'2010». – СПб, 2010. – Т. 2. – С. 342.
5. Новиков В.В., Генович В.В., Гриншпун Д.М. Комплекты визуальных и расчетных лабораторных моделей по основам цифровой электронной обработки информации // Научно-технический вестник информационных технологий, механики и оптики. – 2012. – Вып. 77. – с. 145
6. Новиков В.В. Метод визуализации функционирования электронных схем // Сборник тезисов докладов конгресса молодых ученых, Выпуск 2. Труды молодых ученых / Главный редактор д.т.н., проф. В.О. Никифоров. – СПб: НИУ ИТМО, 2012. – 414 с.
7. Мыльников А.И., Новиков В.В. Комплект визуальных моделей по основам резисторных и диодно-резисторных цепей // Сборник тезисов докладов конгресса молодых ученых, Выпуск 3. Труды молодых ученых. – 2014. – Вып. 3. – с. 154-155. – 315 с.
8. Опадчий Ю.Ф., Глудкин О.П., Гуров А.И. Аналоговая и цифровая электроника (полный курс). – Горячая Линия – Телеком, 2007. – 768 с.
9. Лачин В.И, Савелов Н.С. Электроника. – Феникс, 2010. – 704 с.
10. Gummel H.K., Poon H. C. An integral charge control model of bipolar transistors. // Bell Syst. J., 1970, v. 49, № 5, pp. 827-852.
11. Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники. Том 1. – Питер, 2009. – 512 с.
12. Демирчян К.С., Нейман Л.Р., Коровкин Н.В. Теоретические основы электротехники. Том 2. – Питер, 2009. – 432 с.

References

1. Novikov V.V. Virtual'nyj laboratornyj kompleks po osnovam poluprovodnikovoj cifrovoj jelektroniki // Nauchno-tehnicheskij vestnik SPbGU ITMO. – 2008. – Vyp. 52. – S. 129–133.
2. Grinshpun D.M. Virtual'nye laboratornye kompleksy po osnovam cifrovoj jelektroniki // Trudy XVII Vserossijskoj nauchno-metodicheskoj konferencii «Telematika'2010». – SPb, 2010. – T. 2. – S. 340–342.
3. Grinshpun D.M. Virtual'nye laboratornye kompleksy po osnovam cifrovoj jelektronnoj obrabotki informacii kak sredstvo povyshenija kachestva IT-obrazovanija // Sbornik trudov IV Mezhdunarodnoj nauchnoj konferencii «Sovremennye dostizhenija v nauke i obrazovanii». – Budva, 2010. – S. 12.
4. Novikov V.V., Grinshpun D.M. Interaktivnyj vizual'no-demonstracionnyj virtual'nyj laboratornyj kompleks po osnovam cifrovoj jelektroniki // Trudy XVII Vserossijskoj nauchno-metodicheskoj konferencii «Telematika'2010». – SPb, 2010. – T. 2. – S. 342.
5. Novikov V.V., Genovich V.V., Grinshpun D.M. Komplekty vizual'nyh i raschetnyh laboratornyh modelej po osnovam cifrovoj jelektronnoj obrabotki informacii // Nauchno-tehnicheskij vestnik informacionnyh tehnologij, mehaniki i optiki. – 2012. – Vyp. 77. – s. 145
6. Novikov V.V. Metod vizualizacii funkcionirovanija jelektronnyh shem // Sbornik tezisov dokladov kongressa molodyh uchenyh, Vypusk 2. Trudy molodyh uchenyh / Glavnyj redaktor d.t.n., prof. V.O. Nikiforov. – SPb: NIU ITMO, 2012. – 414 s.
7. Myl'nikov A.I., Novikov V.V. Komplekt vizual'nyh modelej po osnovam rezistornyh i diodno-rezistornyh cepej // Sbornik tezisov dokladov kongressa molodyh uchenyh, Vypusk 3. Trudy molodyh uchenyh. – 2014. – Vyp. 3. – s. 154-155. – 315 s.
8. Opadchij Ju.F., Gludkin O.P., Gurov A.I. Analogovaja i cifrovaja jelektronika (polnyj kurs). – Gorjachaja Linija – Telekom, 2007. – 768 s.
9. Lachin V.I, Savelov N.S. Jelektronika. – Feniks, 2010. – 704 s.
10. Demirchjan K.S., Nejman L.R., Korovkin N.V. Teoreticheskie osnovy jelektrotehniki. Tom 1. – Piter, 2009. – 512 s.
11. Demirchjan K.S., Nejman L.R., Korovkin N.V. Teoreticheskie osnovy jelektrotehniki. Tom 2. – Piter, 2009. – 432 s.